高考新课标1理科数学试题及答案 11页

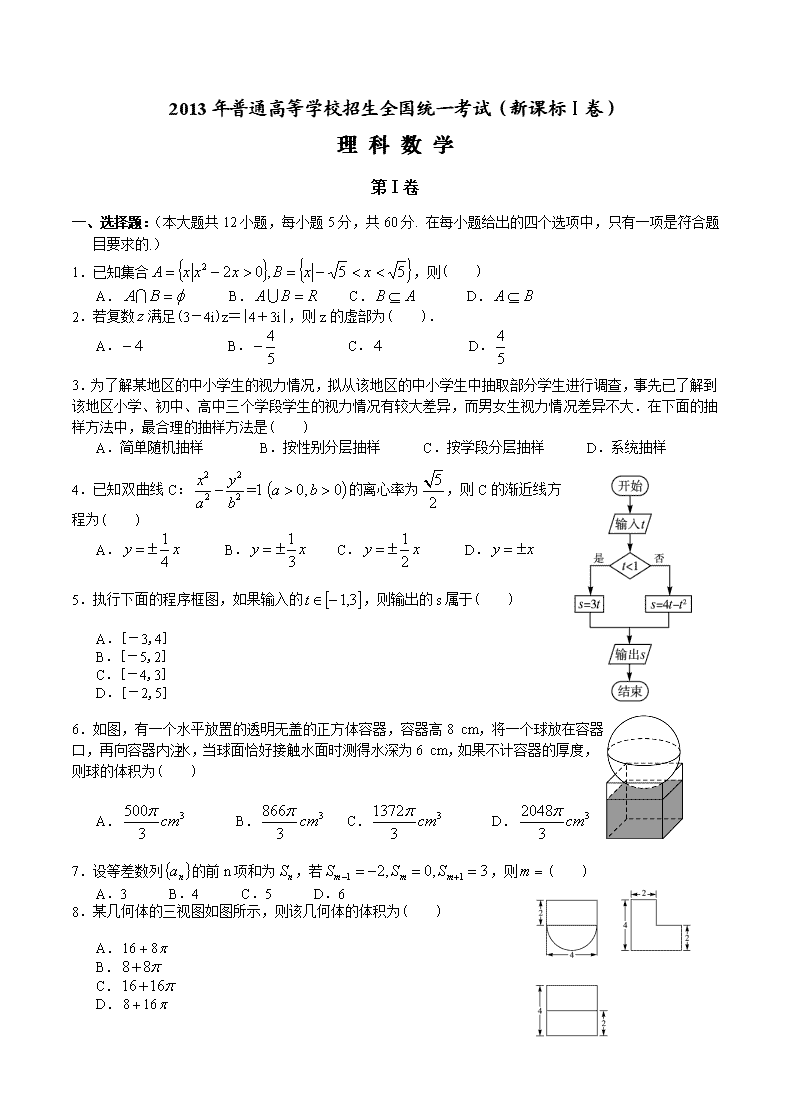
‎2013年普通高等学校招生全国统一考试（新课标Ⅰ卷）‎ 理 科 数 学 第Ⅰ卷 一、选择题：（本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．已知集合，则(　　)‎ A． B． C． D．‎ ‎2．若复数满足(3－4i)z＝|4＋3i|，则z的虚部为(　　)．‎ A． B． C． D．‎ ‎3．为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到 该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是(　　)‎ A．简单随机抽样 B．按性别分层抽样 C．按学段分层抽样 D．系统抽样 ‎4．已知双曲线C：的离心率为，则C的渐近线方程为(　　)‎ A． B． C． D．‎ ‎5．执行下面的程序框图，如果输入的，则输出的s属于(　　)‎ A．[－3,4] ‎ B．[－5,2] ‎ C．[－4,3] ‎ D．[－2,5]‎ ‎6．如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器的厚度，则球的体积为(　　)‎ A． B． C． D．‎ ‎7．设等差数列的前n项和为，若，则(　　)‎ A．3 B．4 C．5 D．6‎ ‎8．某几何体的三视图如图所示，则该几何体的体积为(　　)‎ A． ‎ B． ‎ C． ‎ D．‎ ‎9．设m为正整数，展开式的二项式系数的最大值为，展开式的二项式系数的最大值为.若，则(　　)‎ A．5 B．6 C．7 D．8‎ ‎10．已知椭圆E：的右焦点为，过点的直线交于A，B两点．若AB的中点坐标为，则E的方程为(　　)‎ A． B． C． D．‎ ‎11．已知函数若，则的取值范围是(　　)‎ A． B． C． D．‎ ‎12．设的三边长分别为,的面积为若，，则(　　)‎ A．为递减数列 B．为递增数列 C．为递增数列，为递减数列 D．为递减数列，为递增数列 第Ⅱ卷 本卷包括必考题和选考题两部分. 第13题～第21题为必考题，每个试题考生必须做答. 第22题～第24题为选考题，考生根据要求做答.‎ 二、填空题：（本大题共4小题，每小题5分，共20分.）‎ ‎13. 已知两个单位向量a，b的夹角为60°，c＝ta＋(1－t)b.若b·c＝0，则t＝______.‎ ‎14．若数列的前项和，则的通项公式是_______.‎ ‎15．设当时，函数取得最大值，则__________.‎ ‎16．若函数的图像关于直线对称，则的最大值为__________．‎ 三、解答题：（解答应写出文字说明，证明过程或演算步骤.）‎ ‎17．(本小题满分12分)如图，在中，，，为内一点，.‎ ‎ (1)若，求；‎ ‎(2)若，求.‎ ‎18．(本小题满分12分)如图，三棱柱中，.‎ ‎(1)证明：；‎ ‎(2)若平面⊥平面，，求直线与平面所成角的正弦值．‎ ‎19．(本小题满分12分)一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n.如果n＝3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n＝4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．‎ 假设这批产品的优质品率为50%，即取出的每件产品是优质品的概率都为，且各件产品是否为优质品相互独立．‎ ‎(1)求这批产品通过检验的概率；‎ ‎(2)已知每件产品的检验费用为100元，且抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X(单位：元)，求X的分布列及数学期望．‎ ‎20．(本小题满分12分)已知圆，圆，动圆与圆外切并且与圆内切，圆心的轨迹为曲线.‎ ‎(1)求的方程；‎ ‎(2)是与圆，圆都相切的一条直线，与曲线交于两点，当圆的半径最长时，求.‎ ‎21．(本小题满分12分)设函数．若曲线和曲线都过点，且在点处有相同的切线.‎ ‎(1)求的值；‎ ‎(2)若时，，求的取值范围．‎ 请考生在第22、23题中任选择一题作答，如果多做，则按所做的第一部分，做答时请写清题号.‎ ‎22．（本小题10分）【选修4-4；坐标系与参数方程】‎ 已知曲线的参数方程为(为参数)，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎(1)把的参数方程化为极坐标方程；‎ ‎(2)求与交点的极坐标．‎ ‎23．（本小题10分）【选修4-5；不等式选讲】‎ 已知函数.‎ ‎(1)当时，求不等式的解集；‎ ‎(2)设，且当时，，求的取值范围．‎ ‎2013年普通高等学校夏季招生全国统一考试数学理工农医类 ‎(全国卷I新课标)‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．‎ 答案：B 解析：∵x(x－2)＞0，∴x＜0或x＞2.‎ ‎∴集合A与B可用图象表示为：‎ 由图象可以看出A∪B＝R，故选B.‎ ‎2． ‎ 答案：D 解析：∵(3－4i)z＝|4＋3i|，‎ ‎∴.‎ 故z的虚部为，选D.‎ ‎3．‎ 答案：C 解析：因为学段层次差异较大，所以在不同学段中抽取宜用分层抽样．‎ ‎4．‎ 答案：C 解析：∵，∴.‎ ‎∴a2＝4b2，.‎ ‎∴渐近线方程为.‎ ‎5．‎ 答案：A 解析：若t∈[－1,1)，则执行s＝3t，故s∈[－3,3)．‎ 若t∈[1,3]，则执行s＝4t－t2，其对称轴为t＝2.‎ 故当t＝2时，s取得最大值4.当t＝1或3时，s取得最小值3，则s∈[3,4]．‎ 综上可知，输出的s∈[－3,4]．故选A.‎ ‎6．‎ 答案：A 解析：设球半径为R，由题可知R，R－2，正方体棱长一半可构成直角三角形，即△OBA为直角三角形，如图．‎ BC＝2，BA＝4，OB＝R－2，OA＝R，‎ 由R2＝(R－2)2＋42，得R＝5，‎ 所以球的体积为(cm3)，故选A.‎ ‎7．‎ 答案：C 解析：∵Sm－1＝－2，Sm＝0，Sm＋1＝3，‎ ‎∴am＝Sm－Sm－1＝0－(－2)＝2，am＋1＝Sm＋1－Sm＝3－0＝3.‎ ‎∴d＝am＋1－am＝3－2＝1.‎ ‎∵Sm＝ma1＋×1＝0，∴.‎ 又∵am＋1＝a1＋m×1＝3，∴.‎ ‎∴m＝5.故选C.‎ ‎8．‎ 答案：A 解析：由三视图可知该几何体为半圆柱上放一个长方体，由图中数据可知圆柱底面半径r＝2，长为4，在长方体中，长为4，宽为2，高为2，所以几何体的体积为πr2×4×＋4×2×2＝8π＋16.故选A.‎ ‎9．‎ 答案：B 解析：由题意可知，a＝，b＝，‎ 又∵13a＝7b，∴，‎ 即.解得m＝6.故选B.‎ ‎10． ‎ 答案：D 解析：设A(x1，y1)，B(x2，y2)，∵A，B在椭圆上，‎ ‎∴‎ ‎①－②，得 ‎，‎ 即，‎ ‎∵AB的中点为(1，－1)，∴y1＋y2＝－2，x1＋x2＝2，‎ 而＝kAB＝，∴.‎ 又∵a2－b2＝9，∴a2＝18，b2＝9.‎ ‎∴椭圆E的方程为.故选D.‎ ‎11．‎ 答案：D 解析：由y＝|f(x)|的图象知：‎ ‎①当x＞0时，y＝ax只有a≤0时，才能满足|f(x)|≥ax，可排除B，C.‎ ‎②当x≤0时，y＝|f(x)|＝|－x2＋2x|＝x2－2x.‎ 故由|f(x)|≥ax得x2－2x≥ax.‎ 当x＝0时，不等式为0≥0成立．‎ 当x＜0时，不等式等价于x－2≤a.‎ ‎∵x－2＜－2，∴a≥－2.‎ 综上可知：a∈[－2,0]．‎ ‎12．‎ 答案：B 第Ⅱ卷 本卷包括必考题和选考题两部分．第(13)题～第(21)题为必考题，每个试题考生都必须做答．第(22)题～第(24)题为选考题，考生根据要求做答．‎ 二、填空题：本大题共4小题，每小题5分．‎ ‎13．答案：2‎ 解析：∵c＝ta＋(1－t)b，‎ ‎∴b·c＝ta·b＋(1－t)|b|2.‎ 又∵|a|＝|b|＝1，且a与b夹角为60°，b⊥c，‎ ‎∴0＝t|a||b|cos 60°＋(1－t)，‎ ‎0＝＋1－t.‎ ‎∴t＝2.‎ ‎14．答案：(－2)n－1‎ 解析：∵，①‎ ‎∴当n≥2时，.②‎ ‎①－②，得，‎ 即＝－2.‎ ‎∵a1＝S1＝，‎ ‎∴a1＝1.‎ ‎∴{an}是以1为首项，－2为公比的等比数列，an＝(－2)n－1.‎ ‎15．答案：‎ 解析：f(x)＝sin x－2cos x ‎＝，‎ 令cos α＝，sin α＝，‎ 则f(x)＝sin(α＋x)，‎ 当x＝2kπ＋－α(k∈Z)时，sin(α＋x)有最大值1，f(x)有最大值，‎ 即θ＝2kπ＋－α(k∈Z)，‎ 所以cos θ＝＝＝sin α＝.‎ ‎16．答案：16‎ 解析：∵函数f(x)的图像关于直线x＝－2对称，‎ ‎∴f(x)满足f(0)＝f(－4)，f(－1)＝f(－3)，‎ 即 解得 ‎∴f(x)＝－x4－8x3－14x2＋8x＋15.‎ 由f′(x)＝－4x3－24x2－28x＋8＝0，‎ 得x1＝－2－，x2＝－2，x3＝－2＋.‎ 易知，f(x)在(－∞，－2－)上为增函数，在(－2－，－2)上为减函数，在(－2，－2＋)上为增函数，在(－2＋，＋∞)上为减函数．‎ ‎∴f(－2－)＝[1－(－2－)2][(－2－)2＋8(－2－)＋15]‎ ‎＝(－8－)(8－)‎ ‎＝80－64＝16.‎ f(－2)＝[1－(－2)2][(－2)2＋8×(－2)＋15]‎ ‎＝－3(4－16＋15)‎ ‎＝－9.‎ f(－2＋)＝[1－(－2＋)2][(－2＋)2＋8(－2＋)＋15]‎ ‎＝(－8＋)(8＋)‎ ‎＝80－64＝16.‎ 故f(x)的最大值为16.‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤．‎ ‎17．‎ 解：(1)由已知得∠PBC＝60°，所以∠PBA＝30°.‎ 在△PBA中，由余弦定理得PA2＝.‎ 故PA＝.‎ ‎(2)设∠PBA＝α，由已知得PB＝sin α.‎ 在△PBA中，由正弦定理得，‎ 化简得cos α＝4sin α.‎ 所以tan α＝，即tan∠PBA＝.‎ ‎18．‎ ‎(1)证明：取AB的中点O，连结OC，OA1，A1B.‎ 因为CA＝CB，所以OC⊥AB.‎ 由于AB＝AA1，∠BAA1＝60°，‎ 故△AA1B为等边三角形，‎ 所以OA1⊥AB.‎ 因为OC∩OA1＝O，所以AB⊥平面OA1C.‎ 又A1C平面OA1C，故AB⊥A1C.‎ ‎(2)解：由(1)知OC⊥AB，OA1⊥AB.‎ 又平面ABC⊥平面AA1B1B，交线为AB，‎ 所以OC⊥平面AA1B1B，‎ 故OA，OA1，OC两两相互垂直．‎ 以O为坐标原点，的方向为x轴的正方向，||为单位长，建立如图所示的空间直角坐标系O－‎ xyz.‎ 由题设知A(1,0,0)，A1(0，，0)，C(0,0，)，B(－1,0,0)．‎ 则＝(1,0，)，＝＝(－1，，0)，＝(0，，)．‎ 设n＝(x，y，z)是平面BB1C1C的法向量，‎ 则即可取n＝(，1，－1)．‎ 故cos〈n，〉＝＝.‎ 所以A1C与平面BB1C1C所成角的正弦值为.‎ ‎19．‎ 解：(1)设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，第二次取出的4件产品都是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，这批产品通过检验为事件A，依题意有A＝(A1B1)∪(A2B2)，且A1B1与A2B2互斥，所以 P(A)＝P(A1B1)＋P(A2B2)‎ ‎＝P(A1)P(B1|A1)＋P(A2)P(B2|A2)‎ ‎＝.‎ ‎(2)X可能的取值为400,500,800，并且 P(X＝400)＝，P(X＝500)＝，P(X＝800)＝.‎ 所以X的分布列为 X ‎400‎ ‎500‎ ‎800‎ P EX＝＝506.25.‎ ‎20．‎ 解：由已知得圆M的圆心为M(－1,0)，半径r1＝1；圆N的圆心为N(1,0)，半径r2＝3.‎ 设圆P的圆心为P(x，y)，半径为R.‎ ‎(1)因为圆P与圆M外切并且与圆N内切，‎ 所以|PM|＋|PN|＝(R＋r1)＋(r2－R)＝r1＋r2＝4.‎ 由椭圆的定义可知，曲线C是以M，N为左、右焦点，长半轴长为2，短半轴长为的椭圆(左顶点除外)，其方程为(x≠－2)．‎ ‎(2)对于曲线C上任意一点P(x，y)，由于|PM|－|PN|＝2R－2≤2，‎ 所以R≤2，当且仅当圆P的圆心为(2,0)时，R＝2.‎ 所以当圆P的半径最长时，其方程为(x－2)2＋y2＝4.‎ 若l的倾斜角为90°，则l与y轴重合，可得|AB|＝.‎ 若l的倾斜角不为90°，由r1≠R知l不平行于x轴，设l与x轴的交点为Q，则，可求得Q(－4,0)，所以可设l：y＝k(x＋4)．‎ 由l与圆M相切得，‎ 解得k＝.‎ 当k＝时，将代入，‎ 并整理得7x2＋8x－8＝0，‎ 解得x1,2＝.‎ 所以|AB|＝.‎ 当时，由图形的对称性可知|AB|＝.‎ 综上，|AB|＝或|AB|＝.‎ ‎21．‎ 解：(1)由已知得f(0)＝2，g(0)＝2，f′(0)＝4，g′(0)＝4.‎ 而f′(x)＝2x＋a，g′(x)＝ex(cx＋d＋c)，‎ 故b＝2，d＝2，a＝4，d＋c＝4.‎ 从而a＝4，b＝2，c＝2，d＝2.‎ ‎(2)由(1)知，f(x)＝x2＋4x＋2，g(x)＝2ex(x＋1)．‎ 设函数F(x)＝kg(x)－f(x)＝2kex(x＋1)－x2－4x－2，‎ 则F′(x)＝2kex(x＋2)－2x－4＝2(x＋2)(kex－1)．‎ 由题设可得F(0)≥0，即k≥1.‎ 令F′(x)＝0得x1＝－ln k，x2＝－2.‎ ‎①若1≤k＜e2，则－2＜x1≤0.从而当x∈(－2，x1)时，F′(x)＜0；当x∈(x1，＋∞)时，F′(x)＞0.即F(x)在(－2，x1)单调递减，在(x1，＋∞)单调递增．故F(x)在[－2，＋∞)的最小值为F(x1)．‎ 而F(x1)＝2x1＋2－－4x1－2＝－x1(x1＋2)≥0.‎ 故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．‎ ‎②若k＝e2，则F′(x)＝2e2(x＋2)(ex－e－2)．‎ 从而当x＞－2时，F′(x)＞0，即F(x)在(－2，＋∞)单调递增．‎ 而F(－2)＝0，故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．‎ ‎③若k＞e2，则F(－2)＝－2ke－2＋2＝－2e－2(k－e2)＜0.‎ 从而当x≥－2时，f(x)≤kg(x)不可能恒成立．‎ 综上，k的取值范围是[1，e2]．‎ 请考生在第(22)、(23)、(24)三题中任选一题做答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目计分，做答时请用2B铅笔在答题卡上将所选题号后的方框涂黑．‎ ‎22．‎ ‎ (1)证明：连结DE，交BC于点G.‎ 由弦切角定理得，∠ABE＝∠BCE.‎ 而∠ABE＝∠CBE，故∠CBE＝∠BCE，BE＝CE.‎ 又因为DB⊥BE，‎ 所以DE为直径，∠DCE＝90°，‎ 由勾股定理可得DB＝DC.‎ ‎(2)解：由(1)知，∠CDE＝∠BDE，DB＝DC，‎ 故DG是BC的中垂线，所以BG＝.‎ 设DE的中点为O，连结BO，则∠BOG＝60°.‎ 从而∠ABE＝∠BCE＝∠CBE＝30°，‎ 所以CF⊥BF，故Rt△BCF外接圆的半径等于.‎ ‎23．‎ 解：(1)将消去参数t，化为普通方程(x－4)2＋(y－5)2＝25，‎ 即C1：x2＋y2－8x－10y＋16＝0.‎ 将代入x2＋y2－8x－10y＋16＝0得 ρ2－8ρcos θ－10ρsin θ＋16＝0.‎ 所以C1的极坐标方程为 ρ2－8ρcos θ－10ρsin θ＋16＝0.‎ ‎(2)C2的普通方程为x2＋y2－2y＝0.‎ 由 解得或 所以C1与C2交点的极坐标分别为，.‎ ‎24．‎ 解：(1)当a＝－2时，不等式f(x)＜g(x)化为|2x－1|＋|2x－2|－x－3＜0.‎ 设函数y＝|2x－1|＋|2x－2|－x－3，‎ 则y＝‎ 其图像如图所示．从图像可知，当且仅当x∈(0,2)时，y＜0.‎ 所以原不等式的解集是{x|0＜x＜2}．‎ ‎(2)当x∈时，f(x)＝1＋a.‎ 不等式f(x)≤g(x)化为1＋a≤x＋3.‎ 所以x≥a－2对x∈都成立．‎ 故≥a－2，即.‎ 从而a的取值范围是.‎