安徽省合肥市高考数学二模试卷文科解析版 23页

‎2017年安徽省合肥市高考数学二模试卷（文科）‎ ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知i为虚数单位，则=（　　）‎ A． B． C． D．‎ ‎2．已知集合A={x|1＜x2＜4}，B={x|x﹣1≥0}，则A∩B=（　　）‎ A．（1，2） B．[1，2） C．（﹣1，2） D．[﹣1，2）‎ ‎3．已知命题q：∀x∈R，x2＞0，则（　　）‎ A．命题￢q：∀x∈R，x2≤0为假命题 B．命题￢q：∀x∈R，x2≤0为真命题 C．命题￢q：∃x∈R，x2≤0为假命题 D．命题￢q：∃x∈R，x2≤0为真命题 ‎4．设变量x，y满足约束条件，则目标函数z=x+2y的最大值为（　　）‎ A．5 B．6 C． D．7‎ ‎5．执行如图所示的程序框图，输出的s=（　　）‎ A．5 B．20 C．60 D．120‎ ‎6．设向量满足，则=（　　）‎ A．2 B． C．3 D．‎ ‎7．已知{}是等差数列，且a1=1，a4=4，则a10=（　　）‎ A．﹣ B．﹣ C． D．‎ ‎8．已知椭圆=1（a＞b＞0）的左，右焦点为F1，F2，离心率为e．P是椭圆上一点，满足PF2⊥F1F2，点Q在线段PF1上，且．若=0，则e2=（　　）‎ A． B． C． D．‎ ‎9．已知函数，若f（x1）＜f（x2），则一定有（　　）‎ A．x1＜x2 B．x1＞x2 C． D．‎ ‎10．中国古代数学有着很多令人惊叹的成就．北宋沈括在《梦澳笔谈》卷十八《技艺》篇中首创隙积术．隙积术意即：将木捅一层层堆放成坛状，最上一层长有a个，宽有b个，共计ab个木桶．每一层长宽各比上一层多一个，共堆放n层，设最底层长有c个，宽有d个，则共计有木桶个．假设最上层有长2宽1共2个木桶，每一层的长宽各比上一层多一个，共堆放15层．则木桶的个数为（　　）‎ A．1260 B．1360 C．1430 D．1530‎ ‎11．锐角△ABC中，内角A，B，C的对边分别为a，b，c，且满足（a﹣b）（sinA+sinB）=（c﹣b）sinC，若，则b2+c2的取值范围是（　　）‎ A．（5，6] B．（3，5） C．（3，6] D．[5，6]‎ ‎12．已知函数f（x）=﹣（a+1）x+a（a＞0），其中e为自然对数的底数．若函数y=f（x）与y=f[f（x）]有相同的值域，则实数a的最大值为（　　）‎ A．e B．2 C．1 D．‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．已知双曲线的离心率为，则它的渐近线方程为　　．‎ ‎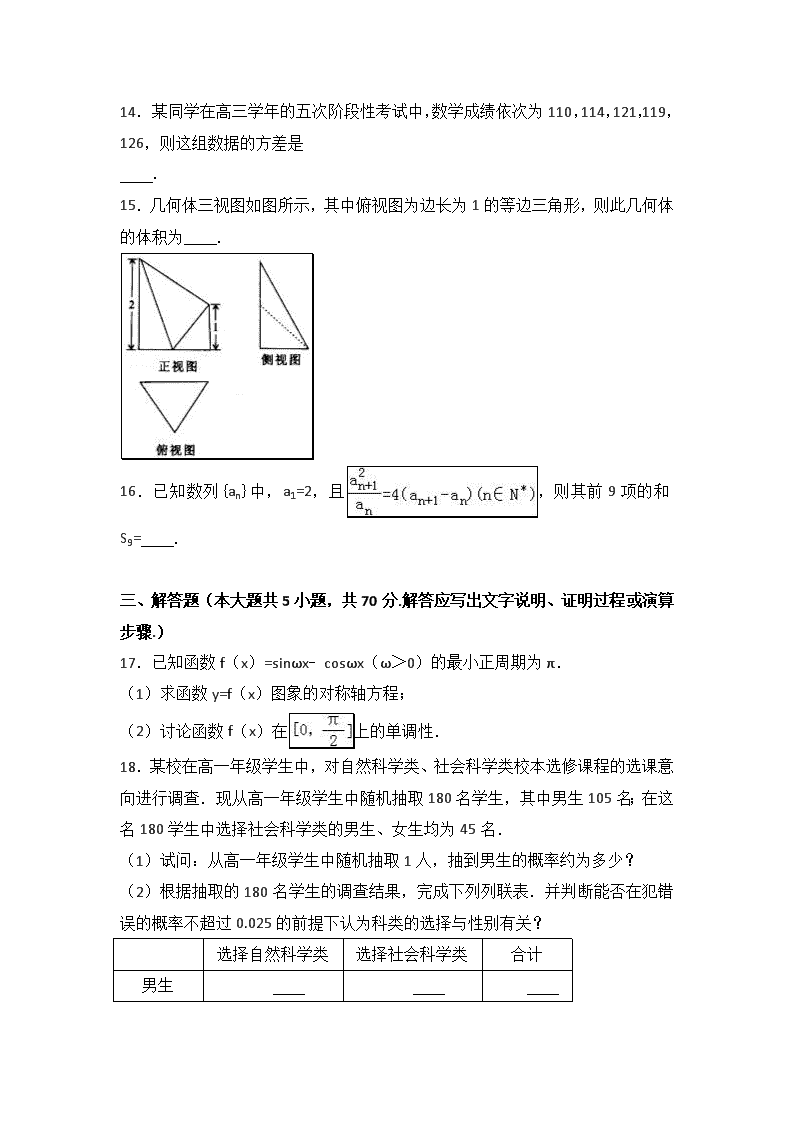14．某同学在高三学年的五次阶段性考试中，数学成绩依次为110，114，121，119，126，则这组数据的方差是 ‎　　．‎ ‎15．几何体三视图如图所示，其中俯视图为边长为1的等边三角形，则此几何体的体积为　　．‎ ‎16．已知数列{an}中，a1=2，且，则其前9项的和S9=　　．‎ ‎　‎ 三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．已知函数f（x）=sinωx﹣cosωx（ω＞0）的最小正周期为π．‎ ‎（1）求函数y=f（x）图象的对称轴方程；‎ ‎（2）讨论函数f（x）在上的单调性．‎ ‎18．某校在高一年级学生中，对自然科学类、社会科学类校本选修课程的选课意向进行调查．现从高一年级学生中随机抽取180名学生，其中男生105名；在这名180学生中选择社会科学类的男生、女生均为45名．‎ ‎（1）试问：从高一年级学生中随机抽取1人，抽到男生的概率约为多少？‎ ‎（2）根据抽取的180名学生的调查结果，完成下列列联表．并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关？‎ 选择自然科学类 选择社会科学类 合计 男生 ‎　　‎ ‎　　‎ ‎　　‎ 女生 ‎　　‎ ‎　　‎ ‎　　‎ 合计 ‎　　‎ ‎　　‎ ‎　　‎ 附：，其中n=a+b+c+d．‎ P（K2≥k0）‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ K0‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎19．如图1，平面五边形ABCDE中，AB∥CE，且，．将△CDE沿CE折起，使点D到P的位置如图2，且，得到四棱锥P﹣ABCE．‎ ‎（1）求证：AP⊥平面ABCE；‎ ‎（2）记平面PAB与平面PCE相交于直线l，求证：AB∥l．‎ ‎20．如图，已知抛物线E：y2=2px（p＞0）与圆O：x2+y2=8相交于A，B两点，且点A的横坐标为2．过劣弧AB上动点P（x0，y0）作圆O的切线交抛物线E于C，D两点，分别以C，D为切点作抛物线E的切线l1，l2，l1与l2相交于点M．‎ ‎（1）求抛物线E的方程；‎ ‎（2）求点M到直线CD距离的最大值．‎ ‎21．已知f（x）=lnx﹣x+m（m为常数）．‎ ‎（1）求f（x）的极值；‎ ‎（2）设m＞1，记f（x+m）=g（x），已知x1，x2为函数g（x）是两个零点，求证：x1+x2＜0．‎ ‎　‎ ‎[选修4-4：坐标系与参数方程]‎ ‎22．在直角坐标系xOy中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cosθ．‎ ‎（1）求出圆C的直角坐标方程；‎ ‎（2）已知圆C与x轴相交于A，B两点，直线l：y=2x关于点M（0，m）（m≠0）对称的直线为l'．若直线l'上存在点P使得∠APB=90°，求实数m的最大值．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎23．已知函数．‎ ‎（1）求函数f（x）的定义域；‎ ‎（2）若当x∈[0，1]时，不等式f（x）≥1恒成立，求实数a的取值范围．‎ ‎　‎ ‎2017年安徽省合肥市高考数学二模试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知i为虚数单位，则=（　　）‎ A． B． C． D．‎ ‎【考点】复数代数形式的乘除运算．‎ ‎【分析】利用复数的运算法则即可得出．‎ ‎【解答】解： ===．‎ 故选：D．‎ ‎　‎ ‎2．已知集合A={x|1＜x2＜4}，B={x|x﹣1≥0}，则A∩B=（　　）‎ A．（1，2） B．[1，2） C．（﹣1，2） D．[﹣1，2）‎ ‎【考点】交集及其运算．‎ ‎【分析】解不等式化简集合A、B，根据交集的定义写出A∩B．‎ ‎【解答】解：集合A={x|1＜x2＜4}={x|﹣2＜x＜﹣1或1＜x＜2}，‎ B={x|x﹣1≥0}={x|x≥1}，‎ 则A∩B={x|1＜x＜2}=（1，2）．‎ 故选：A．‎ ‎　‎ ‎3．已知命题q：∀x∈R，x2＞0，则（　　）‎ A．命题￢q：∀x∈R，x2≤0为假命题 B．命题￢q：∀x∈R，x2≤0为真命题 C．命题￢q：∃x∈R，x2≤0为假命题 D．命题￢q：∃x∈R，x2≤0为真命题 ‎【考点】命题的否定．‎ ‎【分析】本题中的命题是一个全称命题，其否定是特称命题，依据全称命题的否定书写形式写出命题的否定，再进行判断即可．‎ ‎【解答】解：∵命题q：∀x∈R，x2＞0，‎ ‎∴命题￢q：∃x∈R，x2≤0，为真命题．‎ 故选D．‎ ‎　‎ ‎4．设变量x，y满足约束条件，则目标函数z=x+2y的最大值为（　　）‎ A．5 B．6 C． D．7‎ ‎【考点】简单线性规划．‎ ‎【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 联立，解得A（），‎ 化目标函数z=x+2y为y=﹣．‎ 由图可知，当直线y=﹣过A时，直线在y轴上的截距最大，z有最大值为．‎ 故选：C．‎ ‎　‎ ‎5．执行如图所示的程序框图，输出的s=（　　）‎ A．5 B．20 C．60 D．120‎ ‎【考点】程序框图．‎ ‎【分析】先根据已知循环条件和循环体判定循环的规律，然后根据运行的情况判断循环的次数，从而得出所求．‎ ‎【解答】解：第一次循环，s=1，a=5≥3，s=5，a=4；‎ 第二次循环，a=4≥3，s=20，a=3；‎ 第三次循环，a=3≥3，s=60，a=2，‎ 第四次循环，a=2＜3，输出s=60，‎ 故选：C．‎ ‎　‎ ‎6．设向量满足，则=（　　）‎ A．2 B． C．3 D．‎ ‎【考点】平面向量数量积的运算．‎ ‎【分析】可以得到，这样代入即可求出的值，从而得出的值．‎ ‎【解答】解：‎ ‎=‎ ‎=‎ ‎=16﹣4‎ ‎=12；‎ ‎∴．‎ 故选：B．‎ ‎　‎ ‎7．已知{}是等差数列，且a1=1，a4=4，则a10=（　　）‎ A．﹣ B．﹣ C． D．‎ ‎【考点】等差数列的通项公式．‎ ‎【分析】根据题意，设等差数列{}的公差为d，结合题意可得=1， =，计算可得公差d的值，进而由等差数列的通项公式可得的值，求其倒数可得a10的值．‎ ‎【解答】解：根据题意，{}是等差数列，设其公差为d，‎ 若a1=1，a4=4，有=1， =，‎ 则3d=﹣=﹣，即d=﹣，‎ 则=+9d=﹣，‎ 故a10=﹣；‎ 故选：A．‎ ‎　‎ ‎8．已知椭圆=1（a＞b＞0）的左，右焦点为F1，F2，离心率为e．P是椭圆上一点，满足PF2⊥F1F2，点Q在线段PF1上，且．若=0，则e2=（　　）‎ A． B． C． D．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】由题意求得P点坐标，根据向量的坐标运算求得Q点坐标，由=0，求得b4=2c2a2，则b2=a2﹣c2，根据离心率的取值范围，即可求得椭圆的离心率．‎ ‎【解答】解：由题意可知：PF2⊥F1F2，则P（c，），‎ 由，（xQ+c，yQ）=2（c﹣xQ，﹣yQ），则Q（，），‎ ‎=（2c，），=（﹣，），‎ 由=0，则2c×（﹣）+×=0，整理得：b4=2c2a2，‎ 则（a2﹣c2）2=2c2a2，整理得：a4﹣4c2a2+c4=0，则e4﹣4e2+1=0，解得：e2=2±，‎ 由0＜e＜1，则e2=2﹣，‎ 故选C．‎ ‎　‎ ‎9．已知函数，若f（x1）＜f（x2），则一定有（　　）‎ A．x1＜x2 B．x1＞x2 C． D．‎ ‎【考点】三角函数的化简求值；正弦函数的图象．‎ ‎【分析】把已知函数解析式变形，由f（x1）＜f（x2），得sin22x1＞sin22x2，即|sin2x1|＞|sin2x2|，再由x1，x2的范围可得|2x1|＞|2x2|，即|x1|＞|x2|，得到．‎ ‎【解答】解：f（x）=sin4x+cos4x=（sin2x+cos2x）2﹣2sin2xcos2x=．‎ 由f（x1）＜f（x2），得，‎ ‎∴sin22x1＞sin22x2，即|sin2x1|＞|sin2x2|，‎ ‎∵x1∈[﹣]，x2∈[﹣]，‎ ‎∴2x1∈[﹣，]，2x2∈[﹣]，‎ 由|sin2x1|＞|sin2x2|，得|2x1|＞|2x2|，即|x1|＞|x2|，∴．‎ 故选：D．‎ ‎　‎ ‎10．中国古代数学有着很多令人惊叹的成就．北宋沈括在《梦澳笔谈》卷十八《技艺》篇中首创隙积术．隙积术意即：将木捅一层层堆放成坛状，最上一层长有a个，宽有b个，共计ab个木桶．每一层长宽各比上一层多一个，共堆放n层，设最底层长有c个，宽有d个，则共计有木桶个．假设最上层有长2宽1共2个木桶，每一层的长宽各比上一层多一个，共堆放15层．则木桶的个数为（　　）‎ A．1260 B．1360 C．1430 D．1530‎ ‎【考点】等差数列的前n项和．‎ ‎【分析】由已知条件求出a，b，c，d，代入公式能求出结果．‎ ‎【解答】解：∵最上层有长2宽1共2个木桶，每一层的长宽各比上一层多一个，共堆放15层．‎ ‎∴最底层长有c=a+15=17个，宽有d=b+15=16个 则木桶的个数为： =1530．‎ 故选：D．‎ ‎　‎ ‎11．锐角△ABC中，内角A，B，C的对边分别为a，b，c，且满足（a﹣b）（sinA+sinB）=（c﹣b）sinC，若，则b2+c2的取值范围是（　　）‎ A．（5，6] B．（3，5） C．（3，6] D．[5，6]‎ ‎【考点】正弦定理；余弦定理．‎ ‎【分析】由已知利用正弦定理可得b2+c2﹣a2=bc．再利用余弦定理可得cosA，进而可求A，利用正弦定理，三角函数恒等变换的应用化简可得b2+c2=4+2sin（2B﹣），利用B的范围，可求2B﹣‎ 的范围，利用正弦函数的图象和性质可求其范围．‎ ‎【解答】解：∵（a﹣b）（sinA+sinB）=（c﹣b）sinC，由正弦定理可得：（a﹣b）（a+b）=（c﹣b）c，化为b2+c2﹣a2=bc．‎ 由余弦定理可得：cosA===，‎ ‎∴A为锐角，可得A=，‎ ‎∵，‎ ‎∴由正弦定理可得：，‎ ‎∴可得：b2+c2=（2sinB）2+[2sin（﹣B）]2=3+2sin2B+sin2B=4+2sin（2B﹣），‎ ‎∵B∈（，），可得：2B﹣∈（，），‎ ‎∴sin（2B﹣）∈（，1]，可得：b2+c2=4+2sin（2B﹣）∈（5，6]．‎ 故选：A．‎ ‎　‎ ‎12．已知函数f（x）=﹣（a+1）x+a（a＞0），其中e为自然对数的底数．若函数y=f（x）与y=f[f（x）]有相同的值域，则实数a的最大值为（　　）‎ A．e B．2 C．1 D．‎ ‎【考点】利用导数求闭区间上函数的最值．‎ ‎【分析】求出函数的导数，得到函数f（x）的值域，问题转化为即[1，+∞）⊆[，+∞），得到关于a的不等式，求出a的最大值即可．‎ ‎【解答】解：f（x）=﹣（a+1）x+a（a＞0），‎ f′（x）=•ex+ax﹣（a+1），a＞0，‎ 则x＜1时，f′（x）＜0，f（x）递减，‎ x＞1时，f′（x）＞0，f（x）递增，‎ 而x→+∞时，f（x）→+∞，f（1）=，‎ 即f（x）的值域是[，+∞），恒大于0，‎ 而f[f（x）]的值域是[，+∞），‎ 则要求f（x）的范围包含[1，+∞），‎ 即[1，+∞）⊆[，+∞），‎ 故≤1，解得：a≤2，‎ 故a的最大值是2，‎ 故选：B．‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．已知双曲线的离心率为，则它的渐近线方程为　y=±x　．‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】运用离心率公式和a，b，c的关系，可得b==a，即可得到所求双曲线的渐近线方程．‎ ‎【解答】解：由题意可得e==，‎ 即c=a，b==a，‎ 可得双曲线的渐近线方程y=±x，‎ 即为y=±x．‎ 故答案为：y=±x．‎ ‎　‎ ‎14．某同学在高三学年的五次阶段性考试中，数学成绩依次为110，114，121，119，126，则这组数据的方差是 ‎　30.8　．‎ ‎【考点】极差、方差与标准差．‎ ‎【分析】根据平均数与方差的计算公式，计算即可．‎ ‎【解答】解：五次考试的数学成绩分别是110，114，121，119，126，‎ ‎∴它们的平均数是=×=118，‎ 方差是s2= [2+2+2+2+2]=30.8．‎ 故答案为：30.8．‎ ‎　‎ ‎15．几何体三视图如图所示，其中俯视图为边长为1的等边三角形，则此几何体的体积为　　．‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】几何体为四棱锥，棱锥的高为俯视图三角形的高，底面为直角梯形．‎ ‎【解答】解：由三视图可知，几何体为四棱锥，棱锥的高为俯视图中等边三角形的高，棱锥的底面为直角梯形，梯形面积为（1+2）×1=．‎ ‎∴V==．‎ 故答案为．‎ ‎　‎ ‎16．已知数列{an}中，a1=2，且，则其前9项的和S9=　1022　．‎ ‎【考点】数列的求和．‎ ‎【分析】由题意整理可得：an+1=2an，则数列{an}以2为首项，以2为公比的等比数列，利用等比数列的前n项和公式，即可求得S9．‎ ‎【解答】解：由题意可知an+12=4an（an+1﹣an），‎ 则an+12=4（anan+1﹣an2），an+12﹣4anan+1+4an2=0‎ 整理得：（an+1﹣2an）2=0，则an+1=2an，‎ ‎∴数列{an}以2为首项，以2为公比的等比数列，‎ 则前9项的和S9===1022，‎ 故答案为：1022．‎ ‎　‎ 三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．已知函数f（x）=sinωx﹣cosωx（ω＞0）的最小正周期为π．‎ ‎（1）求函数y=f（x）图象的对称轴方程；‎ ‎（2）讨论函数f（x）在上的单调性．‎ ‎【考点】三角函数中的恒等变换应用；正弦函数的图象．‎ ‎【分析】（1）利用辅助角公式化简函数的解析式，根据正弦函数的周期性求得ω，可得其解析式，利用正弦函数的图象的对称求得函数y=f（x）图象的对称轴方程．‎ ‎（2）利用正弦函数的单调性求得函数f（x）在上的单调性．‎ ‎【解答】解：（1）∵，且T=π，∴ω=2．‎ 于是，令，得，‎ 即函数f（x）的对称轴方程为．‎ ‎（2）令，得函数f（x）的单调增区间为．‎ 注意到，令k=0，‎ 得函数f（x）在上的单调增区间为；‎ 同理，求得其单调减区间为．‎ ‎　‎ ‎18．某校在高一年级学生中，对自然科学类、社会科学类校本选修课程的选课意向进行调查．现从高一年级学生中随机抽取180名学生，其中男生105名；在这名180学生中选择社会科学类的男生、女生均为45名．‎ ‎（1）试问：从高一年级学生中随机抽取1人，抽到男生的概率约为多少？‎ ‎（2）根据抽取的180名学生的调查结果，完成下列列联表．并判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关？‎ 选择自然科学类 选择社会科学类 合计 男生 ‎　60　‎ ‎　45　‎ ‎　105　‎ 女生 ‎　30　‎ ‎　45　‎ ‎　75　‎ 合计 ‎　90　‎ ‎　90　‎ ‎　180　‎ 附：，其中n=a+b+c+d．‎ P（K2≥k0）‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ K0‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎【考点】独立性检验的应用．‎ ‎【分析】（1）根据从高一年级学生中随机抽取180名学生，其中男生105名，求出抽到男生的概率；‎ ‎（2）填写2×2列联表，计算观测值K2，对照数表即可得出结论．‎ ‎【解答】解：（1）从高一年级学生中随机抽取1人，抽到男生的概率约为．‎ ‎（2）根据统计数据，可得列联表如下：‎ 选择自然科学类 选择社会科学类 合计 男生 ‎60‎ ‎45‎ ‎105‎ 女生 ‎30‎ ‎45‎ ‎75‎ 合计 ‎90‎ ‎90‎ ‎180‎ ‎，‎ 所以，在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关．‎ ‎　‎ ‎19．如图1，平面五边形ABCDE中，AB∥CE，且，．将△CDE沿CE折起，使点D到P的位置如图2，且，得到四棱锥P﹣ABCE．‎ ‎（1）求证：AP⊥平面ABCE；‎ ‎（2）记平面PAB与平面PCE相交于直线l，求证：AB∥l．‎ ‎【考点】二面角的平面角及求法；直线与平面垂直的判定．‎ ‎【分析】（1）在△CDE中，由已知结合余弦定理得CE．连接AC，可得AC=2．在△PAE中，由PA2+AE2=PE2，得AP⊥AE．同理，AP⊥AC，然后利用线面垂直的判定可得AP⊥平面ABCE；‎ ‎（2）由AB∥CE，且CE⊂平面PCE，AB⊄平面PCE，可得AB∥平面PCE，又平面PAB∩平面PCE=l，结合面面平行的性质可得AB∥l．‎ ‎【解答】证明：（1）在△CDE中，∵，，‎ ‎∴由余弦定理得CE==2．‎ 连接AC，∵AE=2，∠AEC=60°，∴AC=2．‎ 又∵，∴在△PAE中，PA2+AE2=PE2，‎ 即AP⊥AE．‎ 同理，AP⊥AC，‎ ‎∵AC⊂平面ABCE，AE⊂平面ABCE，‎ 且AC∩AE=A，‎ 故AP⊥平面ABCE；‎ ‎（2）∵AB∥CE，且CE⊂平面PCE，AB⊄平面PCE，‎ ‎∴AB∥平面PCE，‎ 又平面PAB∩平面PCE=l，‎ ‎∴AB∥l．‎ ‎　‎ ‎20．如图，已知抛物线E：y2=2px（p＞0）与圆O：x2+y2=8相交于A，B两点，且点A的横坐标为2．过劣弧AB上动点P（x0，y0）作圆O的切线交抛物线E于C，D两点，分别以C，D为切点作抛物线E的切线l1，l2，l1与l2相交于点M．‎ ‎（1）求抛物线E的方程；‎ ‎（2）求点M到直线CD距离的最大值．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】（1）由2pxA=4，p=1．即可求得p的值，求得抛物线方程；‎ ‎（2）分别求得直线l1，l2方程，联立，求得交点M坐标，求得足，，利用点到直线的距离公式，根据函数的单调性即可求得点M到直线CD距离的最大值．‎ ‎【解答】解：（1）由xA=2得，故2pxA=4，p=1．‎ 于是，抛物线E的方程为y2=2x．‎ ‎（2）设，，切线l1：，‎ 代入y2=2x得，由△=0解得，‎ ‎∴l1方程为，同理l2方程为，‎ 联立，解得，‎ 易得CD方程为x0x+y0y=8，其中x0，y0满足，，‎ 联立方程得，则，‎ ‎∴M（x，y）满足，即点M为．‎ 点M到直线CD：x0x+y0y=8的距离，‎ 关于x0单调减，‎ 故当且仅当x0=2时，．‎ ‎　‎ ‎21．已知f（x）=lnx﹣x+m（m为常数）．‎ ‎（1）求f（x）的极值；‎ ‎（2）设m＞1，记f（x+m）=g（x），已知x1，x2为函数g（x）是两个零点，求证：x1+x2＜0．‎ ‎【考点】利用导数研究函数的极值；利用导数研究函数的单调性．‎ ‎【分析】（1）利用导数判断f（x）的单调性，得出f（x）的极值；‎ ‎（2）由g（x1）=g（x2）=0可得，故h（x）=ex﹣x有两解x1，x2，判断h（x）的单调性得出x1，x2的范围，将问题转化为证明h（x1）﹣h（﹣x1）＜0，在判断r（x1）=h（x1）﹣h（﹣x1）的单调性即可得出结论．‎ ‎【解答】解：（1）∵f（x）=lnx﹣x+m，∴，由f'（x）=0得x=1，‎ 且0＜x＜1时，f'（x）＞0，x＞1时，f'（x）＜0．‎ 故函数f（x）的单调递增区间为（0，1），单调递减区间为（1，+∞）．‎ 所以，函数f（x）的极大值为f（1）=m﹣1，无极小值．‎ ‎（2）由g（x）=f（x+m）=ln（x+m）﹣x，‎ ‎∵x1，x2为函数g（x）是两个零点，‎ ‎∴，即，‎ 令h（x）=ex﹣x，则h（x）=m有两解x1，x2．‎ 令h'（x）=ex﹣1=0得x=0，‎ ‎∴﹣m＜x＜0时，h′（x）＜0，当x＞0时，h′（x）＞0，‎ ‎∴h（x）在（﹣m，0）上单调递减，在（0，+∞）上单调递增．‎ ‎∵h（x）=m的两解x1，x2分别在区间（﹣m，0）和（0，+∞）上，‎ 不妨设x1＜0＜x2，‎ 要证x1+x2＜0，‎ 考虑到h（x）在（0，+∞）上递增，只需证h（x2）＜h（﹣x1），‎ 由h（x2）=h（x1）知，只需证h（x1）＜h（﹣x1），‎ 令r（x）=h（x）﹣h（﹣x）=ex﹣2x﹣e﹣x，‎ 则r′（x）=ex+﹣2≥0，‎ ‎∴r（x）单调递增，∵x1＜0，‎ ‎∴r（x1）＜r（0）=0，即h（x1）＜h（﹣x1）成立，‎ 即x1+x2＜0成立．‎ ‎　‎ ‎[选修4-4：坐标系与参数方程]‎ ‎22．在直角坐标系xOy中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cosθ．‎ ‎（1）求出圆C的直角坐标方程；‎ ‎（2）已知圆C与x轴相交于A，B两点，直线l：y=2x关于点M（0，m）（m≠0）对称的直线为l'．若直线l'上存在点P使得∠APB=90°，求实数m的最大值．‎ ‎【考点】简单曲线的极坐标方程．‎ ‎【分析】（1）由ρ=4cosθ得ρ2=4ρcosθ，即可求出圆C的直角坐标方程；‎ ‎（2）l：y=2x关于点M（0，m）的对称直线l'的方程为y=2x+2m，而AB为圆C的直径，故直线l'上存在点P使得∠APB=90°的充要条件是直线l'与圆C有公共点，即可求实数m的最大值．‎ ‎【解答】解：（1）由ρ=4cosθ得ρ2=4ρcosθ，即x2+y2﹣4x=0，即圆C的标准方程为（x﹣2）2+y2=4．‎ ‎（2）l：y=2x关于点M（0，m）的对称直线l'的方程为y=2x+2m，而AB为圆C的直径，故直线l'上存在点P使得∠APB=90°的充要条件是直线l'与圆C有公共点，故，于是，实数m的最大值为．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎23．已知函数．‎ ‎（1）求函数f（x）的定义域；‎ ‎（2）若当x∈[0，1]时，不等式f（x）≥1恒成立，求实数a的取值范围．‎ ‎【考点】函数恒成立问题；函数的定义域及其求法．‎ ‎【分析】（1）由根式内部的代数式大于等于0，求解绝对值的不等式，进一步分类求解含参数的不等式得答案；‎ ‎（2）把不等式f（x）≥1恒成立转化为|ax﹣2|≤3，记g（x）=|ax﹣2|，可得，求解不等式组得答案．‎ ‎【解答】解：（1）要使原函数有意义，则|ax﹣2|≤4，即﹣4≤ax﹣2≤4，得﹣2≤ax≤6，‎ 当a＞0时，解得，函数f（x）的定义域为；‎ 当a＜0时，解得，函数f（x）的定义域为．‎ ‎（2）f（x）≥1⇔|ax﹣2|≤3，记g（x）=|ax﹣2|，‎ ‎∵x∈[0，1]，∴需且只需，即，解得﹣1≤a≤5，‎ 又a≠0，∴﹣1≤a≤5，且a≠0．‎ ‎　‎ ‎2017年4月11日