高考专题突破五圆锥曲线 5页

高考专题突破五　高考中的圆锥曲线问题 考点自测 ‎1．已知双曲线－＝1 (a>0，b>0)和椭圆＋＝1有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为____________．‎ ‎ 2．已知椭圆＋＝1 (a>b>0)与抛物线y2＝2px (p>0)有相同的焦点F，P，Q是椭圆与抛物线的交点，若PQ经过焦点F，则椭圆＋＝1 (a>b>0)的离心率为____________．‎ ‎ 3．若双曲线－＝1的一条渐近线被圆(x－2)2＋y2＝4所截得的弦长为2，则该双曲线的实轴长为(　　)‎ ‎ 4．若双曲线－＝1 (a>0，b>0)的渐近线与抛物线y＝x2＋2有公共点，则此双曲线的离心率的取值范围是(　　)‎ A．[3，＋∞) B．(3，＋∞)‎ C．(1,3] D．(1,3)‎ ‎ 5．设坐标原点为O，抛物线y2＝2x与过焦点的直线交于A、B两点，则·等于(　　)‎ A. B．－ C．3 D．－3‎ 题型一　圆锥曲线中的范围、最值问题 例1　如图所示，在直角坐标系xOy中，点P(1，)到抛物线C：y2＝2px(p>0)的准线的距离为.点M(t,1)是C上的定点，A，B是C上的两动点，且线段AB的中点Q(m，n)在直线OM上．‎ ‎(1)求曲线C的方程及t的值；‎ 5‎ ‎(2)记d＝，求d的最大值．‎ ‎ ‎ ‎　已知点A(－1,0)，B(1,0)，动点M的轨迹曲线C满足∠AMB＝2θ，||·||cos2θ＝3，过点B的直线交曲线C于P，Q两点．‎ ‎(1)求||＋||的值，并写出曲线C的方程；‎ ‎(2)求△APQ面积的最大值．‎ ‎ ‎ 题型二　圆锥曲线中的定点、定值问题 例2　在平面直角坐标系xOy中，已知椭圆＋＝1的左，右顶点分别为A，B，右焦点为F.设过点T(t，m)的直线TA，TB与此椭圆分别交于点M(x1，y1)，N(x2，y2)，其中m>0，y1>0，y2<0.‎ ‎(1)设动点P满足：|PF|2－|PB|2＝4，求点P的轨迹；‎ ‎(2)设x1＝2，x2＝，求点T的坐标；‎ ‎(3)设t＝9，求证：直线MN必过x轴上的一定点(其坐标与m无关)．‎ ‎ ‎ ‎　(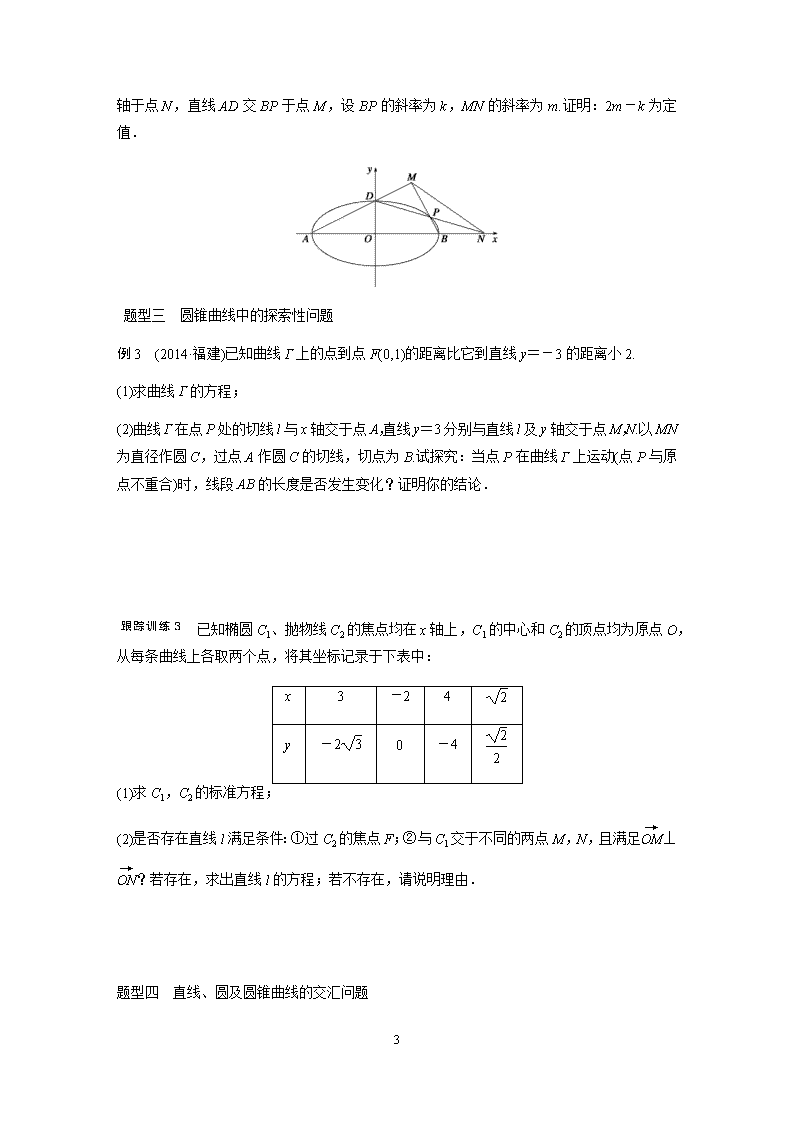2013·江西)椭圆C：＋＝1(a>b>0)的离心率e＝ ，a＋b＝3.‎ ‎(1)求椭圆C的方程；‎ ‎(2)如图所示，A、B、D是椭圆C的顶点，P是椭圆C上除顶点外的任意一点，直线DP交x轴于点N，直线AD交BP于点M，设BP的斜率为k，MN的斜率为m.证明：2m－k为定值．‎ 5‎ ‎ 题型三　圆锥曲线中的探索性问题 例3　(2014·福建)已知曲线Γ上的点到点F(0,1)的距离比它到直线y＝－3的距离小2.‎ ‎(1)求曲线Γ的方程；‎ ‎(2)曲线Γ在点P处的切线l与x轴交于点A，直线y＝3分别与直线l及y轴交于点M，N.以MN为直径作圆C，过点A作圆C的切线，切点为B.试探究：当点P在曲线Γ上运动(点P与原点不重合)时，线段AB的长度是否发生变化？证明你的结论．‎ ‎ ‎ ‎　已知椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点O，从每条曲线上各取两个点，将其坐标记录于下表中：‎ x ‎3‎ ‎－2‎ ‎4‎ y ‎－2 ‎0‎ ‎－4‎ ‎(1)求C1，C2的标准方程；‎ ‎(2)是否存在直线l满足条件：①过C2的焦点F；②与C1交于不同的两点M，N，且满足⊥？若存在，求出直线l的方程；若不存在，请说明理由．‎ ‎ ‎ 题型四　直线、圆及圆锥曲线的交汇问题 例4　(2013·浙江)如图，点P(0，－1)是椭圆C1：＋＝1(a>b>0)的一个顶点，C1的长轴是圆C2：x2＋y2＝4的直径．l1，l2是过点P 5‎ 且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D.‎ ‎(1)求椭圆C1的方程；‎ ‎(2)求△ABD面积取最大值时直线l1的方程．‎ ‎ ‎ ‎　如图，已知圆M：(x－)2＋y2＝，椭圆C：＋＝1 (a>b>0)的右顶点为圆M的圆心，左焦点与双曲线x2－y2＝1的左顶点重合．‎ ‎(1)求椭圆C的方程；‎ ‎(2)已知直线l：y＝kx与椭圆C分别交于两点A，B，与圆M分别交于两点G，H(其中点G在线段AB上)，且|AG|＝|BH|，求k的值．‎ ‎ ‎ ‎(时间：80分钟)‎ ‎1．在平面直角坐标系xOy中，直线l与抛物线y2＝4x相交于不同的A，B两点．‎ ‎(1)如果直线l过抛物线的焦点，求·的值；‎ ‎(2)如果·＝－4，证明：直线l必过一定点，并求出该定点．‎ ‎ ‎ ‎2．已知中心在坐标原点O的椭圆C经过点A(2,3)，且点F(2，0)为其右焦点．‎ ‎(1)求椭圆C的方程；‎ ‎(2)是否存在平行于OA的直线l，使得直线l与椭圆C有公共点，且直线OA与l的距离等于4？若存在，求出直线l的方程；若不存在，说明理由．‎ ‎ ‎ 5‎ ‎3．已知椭圆C：＋＝1 (a>b>0)与双曲线＋＝1 (1