高考文科数学立体几何试题汇编 12页

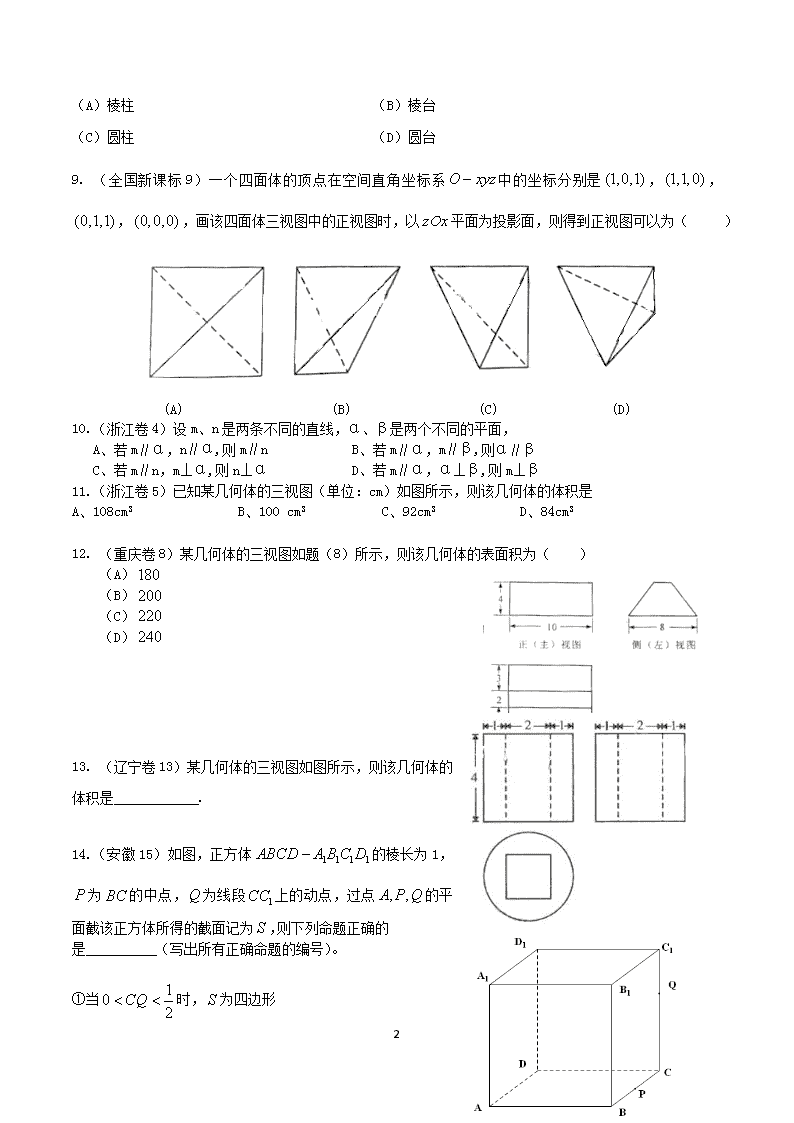
‎1.（北京8）如图，在正方体中，为对角线的三等分点，则到各顶点的距离的不同取值有（ ）‎ A．个 B．个 C．个 D．个 ‎2.（广东卷6）某三棱锥的三视图如图所示，则该三棱锥的体积是( )‎ A． B． ‎ C． D． ‎ ‎3. （广东卷8）设为直线，是两个不同的平面，下列命题中正确的是( )‎ A．若，，则 B．若，，则 C．若，，则 D．若，，则 ‎4. （湖南卷7）已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为的矩形，则该正方体的正视图的面积等于 A． B.1 C. D.‎ ‎5. 江西卷8）.一几何体的三视图如右所示，则该几何体的体积为（ ）‎ A.200+9π B. 200+18π C. 140+9π D. 140+18π ‎ ‎6. （辽宁卷10）已知三棱柱 A． ‎ B． C． D． ‎ B． ‎. （全国卷11）已知正四棱柱的正弦值等于 （A） ‎ （B） （C） （D）‎ ‎8. （四川卷2）一个几何体的三视图如图所示，则该几何体可以是（ ）‎ 12‎ ‎（A）棱柱 （B）棱台 ‎（C）圆柱 （D）圆台 ‎9. （全国新课标9）一个四面体的顶点在空间直角坐标系中的坐标分别是，，，，画该四面体三视图中的正视图时，以平面为投影面，则得到正视图可以为（ ）‎ ‎(A) (B) (C) (D)‎ ‎10.（浙江卷4）设m、n是两条不同的直线，α、β是两个不同的平面，‎ ‎ A、若m∥α，n∥α,则m∥n B、若m∥α，m∥β,则α∥β ‎ ‎ C、若m∥n，m⊥α,则n⊥α D、若m∥α，α⊥β,则m⊥β ‎11.（浙江卷5）已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是 A、108cm3 B、100 cm3 C、92cm3 D、84cm3‎ ‎12. （重庆卷8）某几何体的三视图如题（8）所示，则该几何体的表面积为（ ）‎ ‎（A）‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ ‎13. （辽宁卷13）某几何体的三视图如图所示，则该几何体的体积是 .‎ ‎14.（安徽15）如图，正方体的棱长为1，为的中点，为线段上的动点，过点的平面截该正方体所得的截面记为，则下列命题正确的 是 （写出所有正确命题的编号）。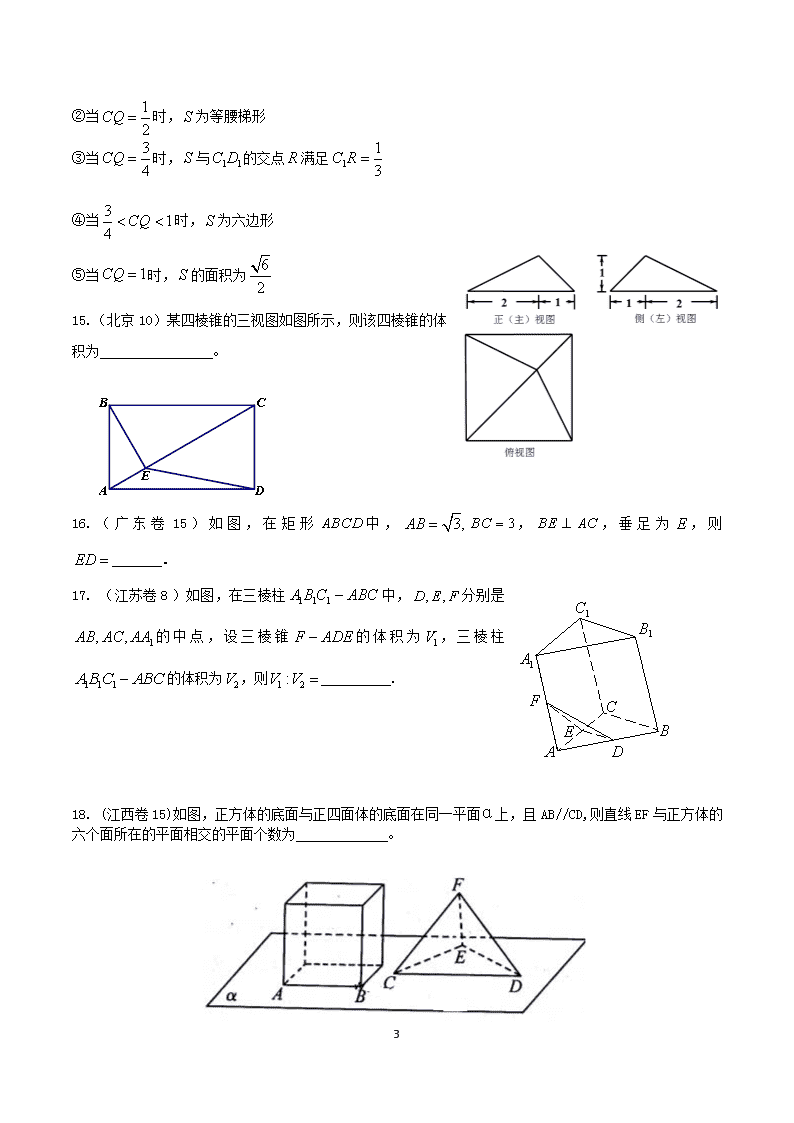‎ ‎①当时，为四边形 12‎ ‎②当时，为等腰梯形 ‎③当时，与的交点满足 ‎④当时，为六边形 ‎⑤当时，的面积为 ‎15.（北京10）某四棱锥的三视图如图所示，则该四棱锥的体积为 。 ‎ ‎16.（广东卷15）如图，在矩形中，，，垂足为，则 ．‎ ‎17. （江苏卷8）如图，在三棱柱中，分别是的中点，设三棱锥的体积为，三棱柱的体积为，则 .‎ ‎18. (江西卷15)如图，正方体的底面与正四面体的底面在同一平面α上，且AB//CD,则直线EF与正方体的六个面所在的平面相交的平面个数为 。‎ 12‎ ‎19. （全国卷16）已知圆和圆是球的大圆和小圆，其公共弦长等于球的半径，则球的表面积等于 .‎ ‎20. （陕西卷12）某几何体的三视图如图所示, 则其表面积为 . ‎ ‎21. （天津卷10）已知一个正方体的所有顶点在一个球面上. 若球的体积为, 则正方体的棱长为 .‎ ‎22. （全国新课标15）已知正四棱锥的体积为，底面边长为，则以为球心，为半径的球的表面积为________。‎ ‎23.（安徽18）如图，四棱锥的底面是边长为2的菱形，.‎ 已知 .‎ ‎（Ⅰ）证明：‎ ‎（Ⅱ）若为的中点，求三菱锥的体积.‎ ‎24.（北京17）如图，在四棱锥中，，，，平面底面，，和分别是和的中点，求证：‎ ‎（1）底面 ‎（2）平面 ‎（3）平面平面 12‎ ‎25.（福建18）如图，在四棱锥中，，，，，，，．‎ ‎（1）当正视图方向与向量的方向相同时，画出四棱锥的正视图.（要求标出尺寸，并画出演算过程）；‎ ‎（2）若为的中点，求证：；‎ ‎（3）求三棱锥的体积．‎ ‎ ‎ ‎26.（广东卷18）如图4，在边长为1的等边三角形中，分别是边上的点，‎ ‎，是的中点，与交于点，将沿折起，‎ 得到如图5所示的三棱锥，其中．‎ ‎(1) 证明：//平面；‎ ‎(2) 证明：平面； ‎ ‎(3) 当时，求三棱锥的体积．‎ 12‎ ‎27.（湖南卷17）如图，在直菱柱ABC-A1B1C1中，∠ABC=90°，AB=AC=，AA1=3，D是BC的中点，点E在菱BB1上运动。‎ （I） 证明：AD⊥C1E；‎ （II） 当异面直线AC，C1E 所成的角为60°时，‎ 求三菱锥C1-A2B1E的体积 ‎28.（江苏卷16）如图，在三棱锥中，平面平面，,. 过作，垂足为，点,分别是侧棱,的中点.‎ 求证：(1) 平面平面;‎ ‎(2) .‎ 12‎ ‎（‎ ‎29.（江西卷19）如图，直四棱柱ABCD – A1B1C1D1中，AB//CD，AD⊥AB，AB=2，AD=，AA1=3，E为CD上一点，DE=1，EC=3‎ （1） 证明：BE⊥平面BB1C1C;‎ （2） 求点B1 到平面EA1C1 的距离 ‎30.（辽宁卷18）如图，‎ ‎（I）求证：‎ ‎（II）设 12‎ ‎31.（全国卷19）如图，四棱锥都是边长为的等边三角形.‎ ‎（I）证明：‎ ‎（II）求点 ‎ ‎32.（陕西卷18）如图, 四棱柱ABCD－A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, . ‎ ‎ (Ⅰ) 证明: A1BD // 平面CD1B1; ‎ ‎ (Ⅱ) 求三棱柱ABD－A1B1D1的体积. ‎ 12‎ ‎33.（四川卷19）如图，在三棱柱中，侧棱底面，，，分别是线段的中点，是线段上异于端点的点。‎ ‎（Ⅰ）在平面内，试作出过点与平面平行的直线，说明理由，并证明直线平面；‎ ‎（Ⅱ）设（Ⅰ）中的直线交于点，求三棱锥的体积。（锥体体积公式：，其中为底面面积，为高）‎ ‎34.（天津卷17）如图, 三棱柱ABC－A1B1C1中, 侧棱A1A⊥底面ABC,且各棱长均相等. D, E, F分别为棱AB, BC, A1C1的中点. ‎ 12‎ ‎(Ⅰ) 证明EF//平面A1CD; ‎ ‎(Ⅱ) 证明平面A1CD⊥平面A1ABB1; ‎ ‎(Ⅲ) 求直线BC与平面A1CD所成角的正弦值. ‎ ‎35.（全国新课标18）如图，直三棱柱中，，分别是，的中点，‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）设，，求三棱锥的体积。‎ 12‎ ‎36.（浙江卷19）如图，在在四棱锥P-ABCD中，PA⊥面ABCD，AB=BC=2，‎ ‎ AD=CD=，PA=，∠ABC=120°,G为线段PC上的点.‎ ‎（Ⅰ）证明：BD⊥面PAC ; ‎ ‎（Ⅱ)若G是PC的中点，求DG与PAC所成的角的正切值；‎ ‎（Ⅲ）若G满足PC⊥面BGD，求 的值.‎ ‎37.（重庆卷19）如图，四棱锥中，⊥底面，，， ．‎ ‎（Ⅰ）求证：⊥平面；‎ ‎（Ⅱ）若侧棱上的点满足，求三棱锥的体积．‎ 12‎ ‎38．如图，某地质队自水平地面A，B，C三处垂直向地下钻探，自A点向下钻到A1处发现矿藏，再继续下钻到A2处后下面已无矿，从而得到在A处正下方的矿层厚度为．同样可得在B，C处正下方的矿层厚度分别为，，且. 过，的中点，且与直线平行的平面截多面体所得的截面为该多面体的一个中截面，其面积记为．‎ ‎（Ⅰ）证明：中截面是梯形；‎ ‎（Ⅱ）在△ABC中，记，BC边上的高为，面积为. 在估测三角形区域内正下方的矿藏储量（即多面体的体积）时，可用近似公式来估算. 已知，试判断与V的大小关系，并加以证明. ‎ 12‎