山西省各地市高考数学联考试题分类汇编 立体几何 7页

‎ 山西省各地市2011年高考数学最新联考试题分类大汇编第8部分:立体几何 一、选择题：‎ ‎11．(山西省太原市2011年高三模拟一理科）在以正方体的顶点为端点的线段中任取n条线段，使得其中任意两条线段所在直线都是异面直线，则n的最大值为 （ A ）‎ ‎ A．4 B．‎6 ‎C．8 D．12‎ ‎8．(山西省太原市2011年高三模拟一文科已知直线，给出四个命题：‎ ‎ ①若，则 ②若 ‎ ③若 ④若 ‎ 其中真命题的个数是 （ C ）‎ ‎ A．4 B．‎3 ‎C．2 D．1‎ ‎10. (山西省大同市2011届高三第一次模拟理科)某几何体的直观图如右图所示，则该几何体的侧（左）视图的面积为( B )‎ A. B.[来源:Zxxk.Com]‎ C. 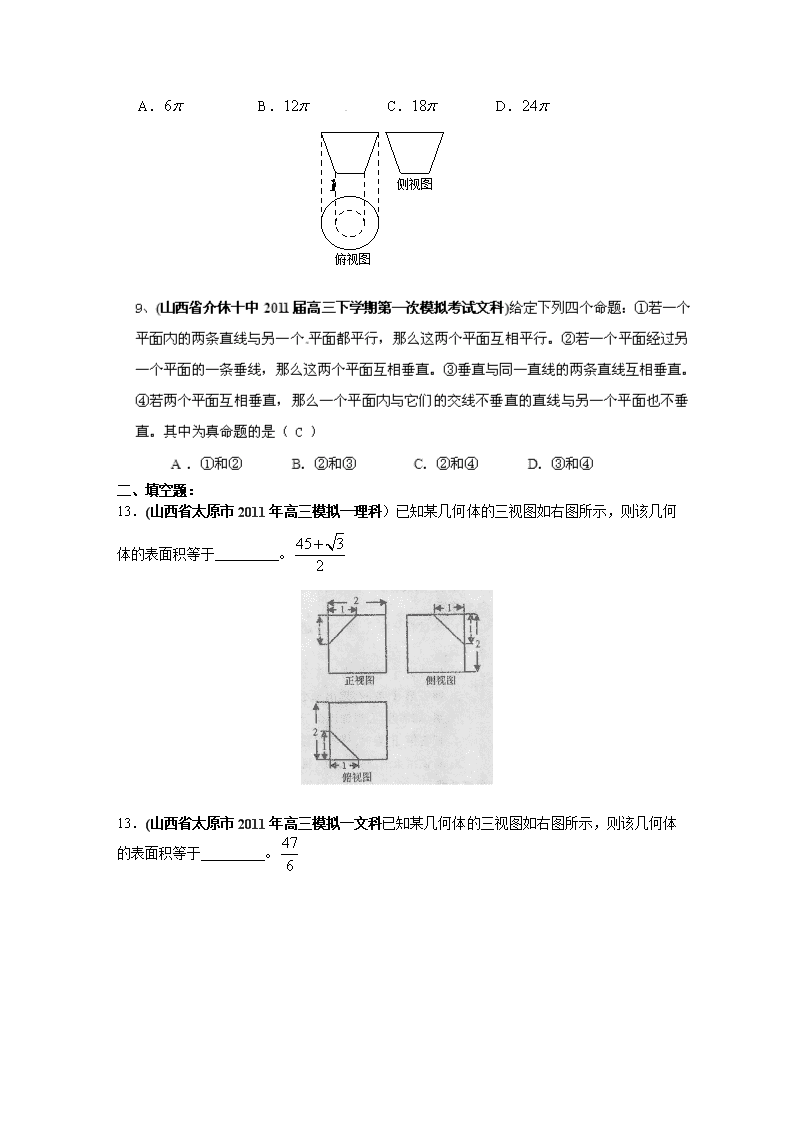D.‎ ‎11．(山西省2011届高三第三次四校联考文科)一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为 ( C )‎ A． B． ‎ C．　 D．‎ 正视图 侧视图 俯视图 ‎3．(山西大学附属中学2011年高三模拟考试理科)右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是( B )‎ A． B． C． D． ‎ 二、填空题：‎ ‎13．(山西省太原市2011年高三模拟一理科）已知某几何体的三视图如右图所示，则该几何体的表面积等于 。‎ ‎13．(山西省太原市2011年高三模拟一文科已知某几何体的三视图如右图所示，则该几何体的表面积等于 。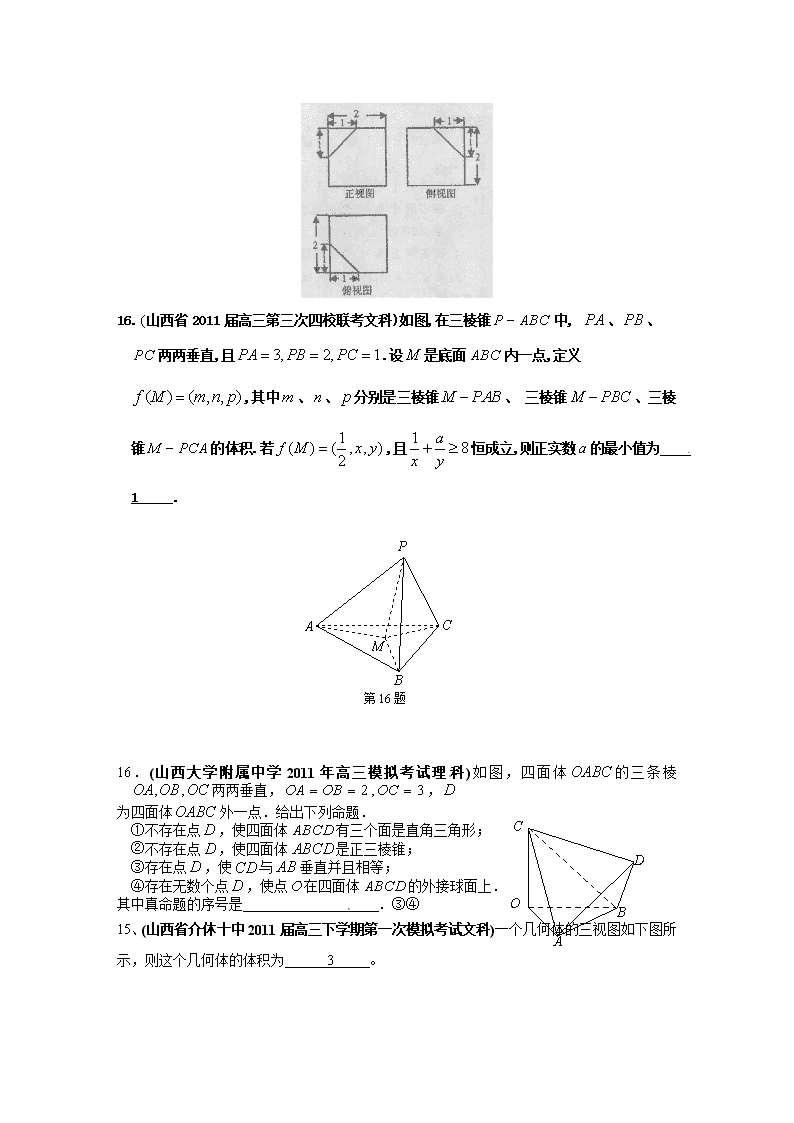‎ ‎16. (山西省2011届高三第三次四校联考文科)如图,在三棱锥中, 、、两两垂直,且.设是底面内一点,定义,其中、、分别是三棱锥、 三棱锥、三棱锥的体积.若,且恒成立,则正实数的最小值为 1 .‎ 第16题 ‎16．(山西大学附属中学2011年高三模拟考试理科)如图，四面体的三条棱两两垂直，,，‎ O A B D C 为四面体外一点．给出下列命题．‎ ‎①不存在点，使四面体有三个面是直角三角形；‎ ‎②不存在点，使四面体是正三棱锥；‎ ‎③存在点，使与垂直并且相等；‎ ‎④存在无数个点，使点在四面体的外接球面上．‎ 其中真命题的序号是 ．③④‎ ‎15、(山西省介休十中2011届高三下学期第一次模拟考试文科)一个几何体的三视图如下图所示，则这个几何体的体积为 3 。‎ 三、解答题：‎ ‎19. (山西省2011届高三第三次四校联考文科) (本小题满分12分)‎ 如图，为圆的直径，点、在圆上，，矩形所在的平面和圆所在的平面互相垂直，且，.‎ ‎（1）求证：平面；‎ ‎（2）设的中点为，求证：平面；‎ ‎（3）设平面将几何体分成的两个锥 ‎ 体的体积分别为，，求．‎ ‎19.(本小题满分12分)‎ 解析：（1）证明： 平面平面,,‎ 平面平面=，‎ 平面， [来源:学+科+网Z+X+X+K]‎ 平面， ,………　2分 又为圆的直径，， ……………………　3分 平面。 ……………………　4分 ‎（2）设的中点为，则，又，‎ 则，为平行四边形， …………………　6分 ‎ ‎，又平面，平面，‎ 平面。 …………………　8分 ‎(3)过点作于，平面平面，‎ 平面，， ………………　10分 ‎ 平面，‎ ‎，………………11分 ‎ ‎． ……………………12分 ‎18．(山西大学附属中学2011年高三模拟考试理科)（本小题满分12分）‎ 如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，‎ E、F分别为棱BC、AD的中点．‎ ‎（Ⅰ）若PD=1，求异面直线PB和DE所成角的余弦值．‎ ‎（Ⅱ）若二面角P-BF-C的余弦值为，求四棱锥P-ABCD 的体积． ‎ ‎[来源:学.科.网]‎ 解：（Ⅰ）E，F分别为棱BC，AD的中点，ABCD是边长为2的正方形 Þ∥且=Þ为平行四边形 Þ ∥Þ的所成角．‎ 中，BF= ,PF=，PB=3Þ Þ异面直线PB和DE所成角的余弦为 ‎（Ⅱ）以D为原点，射线DA,DC,DP分别为x,y,z轴建立空间 直角坐标系.设PD=a,‎ 可得如下点的坐标： P(0,0,a),F(1,0,0),B(2,2,0)，则有： ‎ ‎ 因为PD⊥底面ABCD，所以平面ABCD的一个法向量为， ‎ 设平面PFB的一个法向量为，则可得 即 ‎ ‎ 令x=1,得，所以. 由已知，二面角P-BF-C的余弦值为，所以得：， 解得．‎ ‎ 因为PD是四棱锥P-ABCD的高，所以，其体积为．‎ ‎[来源:学。科。网]‎ ‎18．(山西大学附属中学2011年高三模拟考试文科)（本小题满分12分）‎ A B C D F E 如图所示，正方形与直角梯形所在平面互相垂直，，，.‎ ‎(Ⅰ)求证：平面；‎ ‎（Ⅱ）求四面体的体积.‎ A B C G F E D O ‎18．（本小题满分12分）‎ ‎(Ⅰ)证明：设，取中点，连结，‎ 所以，. ‎ 因为，，所以， ‎ 从而四边形是平行四边形，. [来源:Z§xx§k.Com]‎ 因为平面,平面, ‎ 所以平面，即平面. ‎ ‎（Ⅱ）解：因为平面平面，,‎ 所以平面. ‎ 因为,,，‎ 所以的面积为， ‎ 所以四面体的体积. ‎ ‎[来源:学+科+网]‎ ‎20、(山西省介休十中2011届高三下学期第一次模拟考试文科)（本小题满分12分）如图所示，在正三棱柱中，底面边长和侧棱都是2，D是侧棱上任意一点．E是的中点．‎ ‎（1）求证： 平面ABD；‎ ‎（2）求证： ；‎ ‎（3）求三棱锥的体积。‎ ‎20、（1）证明：由正三棱柱的性质知，‎ 因为平面ABD，‎ 平面ABD 所以平面ABD 4分 ‎（2）解：设AB中点为G，连，‎ ‎ ∵为正三角形，且G为中点，∴‎ 又 则， ∴‎ ‎，所以， ‎ 而平面 所以 8分 ‎（3）由题意可知：‎ ‎ 12分