高考文科数学集合专题讲解及高考真题精选含答案 4页

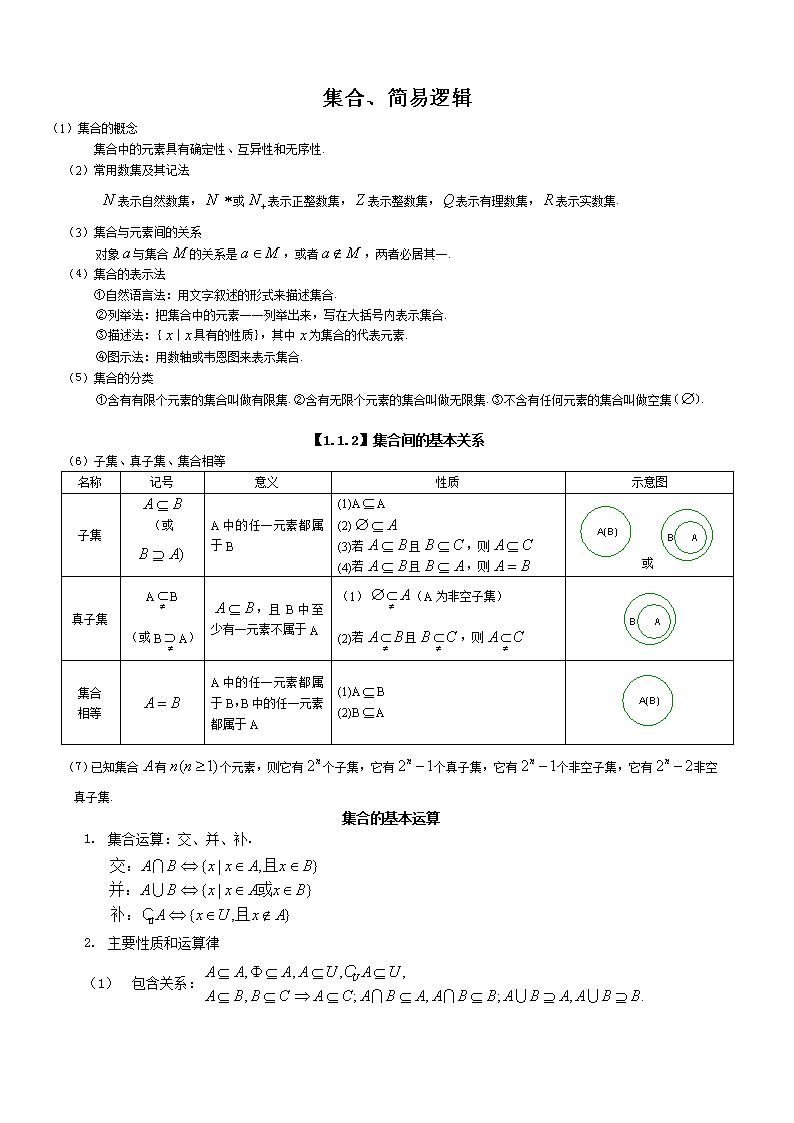
集合、简易逻辑 ‎（1）集合的概念 ‎ 集合中的元素具有确定性、互异性和无序性.‎ ‎（2）常用数集及其记法 表示自然数集，或表示正整数集，表示整数集，表示有理数集，表示实数集.‎ ‎（3）集合与元素间的关系 对象与集合的关系是，或者，两者必居其一.‎ ‎（4）集合的表示法 ‎ ①自然语言法：用文字叙述的形式来描述集合.‎ ‎②列举法：把集合中的元素一一列举出来，写在大括号内表示集合.‎ ‎③描述法：{|具有的性质}，其中为集合的代表元素.‎ ‎④图示法：用数轴或韦恩图来表示集合.‎ ‎（5）集合的分类 ‎①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集().‎ ‎【1.1.2】集合间的基本关系 ‎（6）子集、真子集、集合相等 名称 记号 意义 性质 示意图 子集 ‎（或 A中的任一元素都属于B ‎(1)AA ‎(2)‎ ‎(3)若且，则 ‎(4)若且，则 或 真子集 AB ‎（或BA）‎ ‎，且B中至少有一元素不属于A ‎（1）（A为非空子集）‎ ‎(2)若且，则 集合 相等 A中的任一元素都属于B，B中的任一元素都属于A ‎(1)AB ‎(2)BA ‎（7）已知集合有个元素，则它有个子集，它有个真子集，它有个非空子集，它有非空真子集.‎ 集合的基本运算 1. 集合运算：交、并、补.‎ 2. 主要性质和运算律 （1） 包含关系：‎ （1） 等价关系：‎ （2） 集合的运算律：‎ 交换律： ‎ 结合律: ‎ 分配律:.‎ ‎0-1律：‎ 等幂律：‎ 求补律：A∩CUA=φ A∪CUA=U ðCUU=φ ðCUφ=U ‎ 反演律：CU(A∩B)= (CUA)∪(CUB) CU(A∪B)= (CUA)∩(CUB)‎ 简易逻辑 ‎1、命题的定义：可以判断真假的语句叫做命题。‎ ‎2、逻辑联结词、简单命题与复合命题：‎ ‎“或”、“且”、“非”这些词叫做逻辑联结词；不含有逻辑联结词的命题是简单命题；由简单命题和逻辑联结词“或”、“且”、“非”构成的命题是复合命题。‎ 构成复合命题的形式：p或q(记作“p∨q” )；p且q(记作“p∧q” )；非p(记作“┑q” ) 。‎ ‎3、“或”、 “且”、 “非”的真值判断 ‎（1）“非p”形式复合命题的真假与F的真假相反；‎ ‎（2）“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；‎ ‎（3）“p或q”形式复合命题当p与q同为假时为假，其他情况时为真．‎ ‎4、四种命题的形式：‎ 原命题：若P则q； 逆命题：若q则p；‎ 否命题：若┑P则┑q；逆否命题：若┑q则┑p。‎ ‎(1)交换原命题的条件和结论，所得的命题是逆命题；‎ ‎ (2)同时否定原命题的条件和结论，所得的命题是否命题；‎ ‎ (3)交换原命题的条件和结论，并且同时否定，所得的命题是逆否命题．‎ ‎5、四种命题之间的相互关系：‎ 一个命题的真假与其他三个命题的真假有如下三条关系：(原命题逆否命题)‎ ‎①、原命题为真，它的逆命题不一定为真。‎ ‎②、原命题为真，它的否命题不一定为真。‎ ‎③、原命题为真，它的逆否命题一定为真。‎ ‎6、如果已知pq那么我们说，p是q的充分条件，q是p的必要条件。‎ 若pq且qp,则称p是q的充要条件，记为p⇔q.‎ ‎09-13高考真题 ‎09.3.“sin=”是“”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 ‎【答案】A ‎09.13. 设集合A=(x∣log2x<1), B=(X∣<1), 则A= .‎ ‎【答案】‎ ‎【解析】易得A= B= ∴A∩B=.‎ ‎10.1设集合M={1,2,4,8},N={x|x是2的倍数}，则M∩N=C A. ‎{2,4} B.{1,2,4} C.{2,4,8} D{1,2,8}‎ ‎10.10.记实数…中的最大数为{…}，最小数为min{…}.已知的三边边长为、、（）,定义它的倾斜度为则“t=1”是“为等边三解形”的B A,充分布不必要的条件 B.必要而不充分的条件 C.充要条件 D.既不充分也不必要的条件 ‎11.1．已经，，，则CU A． B． C． D．‎ ‎【详细解析】 先求出={1,2,3,4,5,7}，再求 CU ‎【考点定位】 考查集合的并集，补集的运算,属于简单题.‎ ‎11.10．若实数，满足，，且，则称a与b互补．记，那么是与互补的 A．必要而不充分的条件 B．充分而不必要的条件 C．充要条件 D．既不充分也不必要的条件 ‎【详细解析】 若(a,b)= ，则=（a+b）‎ ‎ 两边平方解得ab=0，故a，b至少有一为0，不妨令a=0则可得|b|-b=0，故b≥0，即a与b互补，而当a与b互补时，易得ab=0，此时=0，即(a,b)=0，故(a,b)=0是a与b互补的充要条件.‎ ‎【考点定位】 本题考查的知识点是必要条件、充分条件与充要条件的，其中判断φ（a，b）=0⇒a与b互补与a与b互补⇒φ（a，b）=0的真假，是解答本题的关键．属于中档题 ‎12.1.已知集合,则满足条件的集合的个数为( D )‎ A.1 B.2 C.3 D.4‎ ‎12.9.设,则是的( A )‎ A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 ‎13.1．已知全集，集合，，则 A． B． C． D．‎ ‎1．B ‎ ‎13.3．在一次跳伞训练中，甲、乙两位学员各跳一次．设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为 A．∨ B．∨ C．∧ D．∨‎ A 因为p是“甲降落在指定范围”，q是“乙降落在指定范围”，则是“没有降落在指定范围”，是“乙没有降落在指定范围”，所以命题“至少有一位学员没有降落在指定范围”可表示为∨ .‎