备战高考数学优质试卷分项版第02期专题02函数文 15页

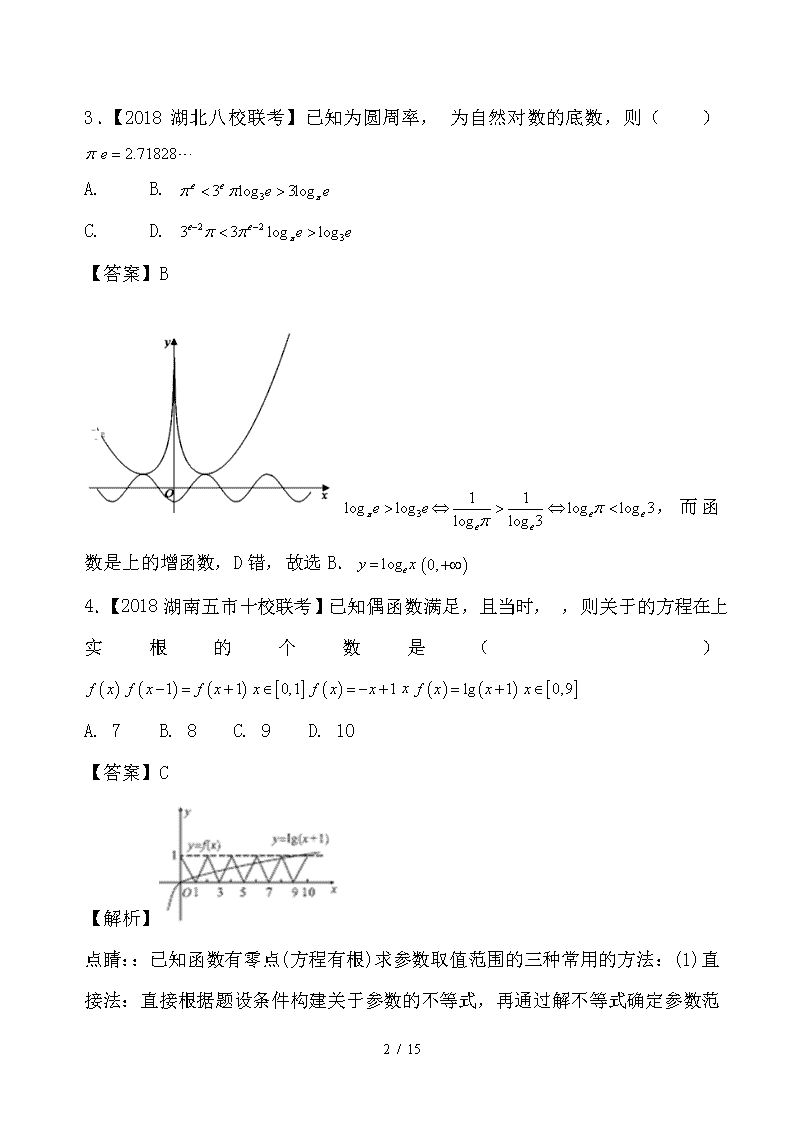
‎【2019最新】精选备战高考数学优质试卷分项版第02期专题02函数文 一、选择题 ‎1．【2018湖北咸宁联考】若函数（，且）的值域是，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎2．【2018湖北八校联考】已知函数与有两个公共点，则在下列函数中满足条件的周期最大的函数（　　）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】定义域为，①当时， ， ，令，解得，由，得，由，得，∴当时， .又是偶函数，∴图象关于轴对称， ，∵只有个公共点，∴最大值为1．则最长周期为，即，即，则，∴，解得，故周期最大的，故选A．‎ ‎3．【2018湖北八校联考】已知为圆周率， 为自然对数的底数，则（ ）‎ 15 / 15‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎，而函数是上的增函数，D错，故选B．‎ ‎4．【2018湖南五市十校联考】已知偶函数满足，且当时， ，则关于的方程在上实根的个数是（ ）‎ A. 7 B. 8 C. 9 D. 10‎ ‎【答案】C ‎【解析】‎ 15 / 15‎ 点睛：：已知函数有零点(方程有根)求参数取值范围的三种常用的方法：(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．一是转化为两个函数的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，二是转化为的交点个数的图象的交点个数问题 .‎ ‎5．【2018湖南五校联考】已知函数，，设为实数，若存在实数，使，则实数的取值范围为 A. B. C. D. ‎ ‎【答案】C ‎【解析】因为，.‎ 函数,,‎ 点睛：对于方程解的个数(或函数零点个数)问题，可利用函数的值域或最值，结合函数的单调性、草图确定其中参数范围．从图象的最高点、最低点，分析函数的最值、极值；从图象的对称性，分析函数的奇偶性；从图象的走向趋势，分析函数的单调性、周期性等．‎ ‎6．【2018黑龙江齐齐哈尔八中二模】已知函数，则（ ）‎ A. 4 B. 2 C. 1 D. 0‎ ‎【答案】A ‎【解析】由于函数的解析式可得：‎ ‎.‎ 本题选择A选项.‎ 15 / 15‎ ‎7．【2018衡水联考】已知函数在区间上为增函数，且是上的偶函数，若，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D 点睛：本题主要考查函数的单调性与对称性.根据题意，函数关于轴对称，且在轴左右两侧单调性相反，即左增右减，距离对称轴越远，函数值就越小，所以原不等式比较两个函数值的大小，转化为比较两个自变量与2的差的绝对值的大小，绝对值大的，距离轴远，函数值就小.‎ ‎8．【2018吉林乾安七中三模】已知函数若函数恰有个零点，则的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】（1）当时， ,g(x)=0,变形为，所以时，有一解， 无解。‎ ‎（2）当时，g(x)= ，g(x)=0,解得x=0,`‎ ‎（3）当时， ，若，g(x)=0，则，令 ， ，函数h(x)在单调递减，在单调递增。，‎ 当时，此时有两解，当时，有一解，当时，无解。‎ 15 / 15‎ 综上所述， 有三个零点， 有两个零点， ，有一个零点， 时，有两个零点，选B ‎【点睛】‎ 分段函数的处理常用分段讨论和数形结合，零点问题也常用数形结合及分离参数，所以本题以分段讨论切入，再结合分离参数及导数分析。‎ ‎9．【2018吉林乾安七中三模】函数在的图象为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【点睛】对于函数图像选择题，一般从四个选项的图像差异性入手讨论函数的性质，从整体性质到局部性质，如本题先利用图像对称性，考虑奇偶性，再考虑对称轴。再利用导数分析函数f(x)在的最值问题。‎ ‎10．【2018陕西西安××区联考】已知定义在R上的函数满足，在区间上是增函数，且函数为奇函数，则 A. B. ‎ C. D. ‎ ‎【答案】A ‎【点睛】本题考查函数的奇偶性与单调性的综合应用，解题时求出函数的周期与对称中心是解题的关键 ‎11．【2018陕西西安××区联考】已知且，则 15 / 15‎ A. -1 B. 2 C. 3 D. -3‎ ‎【答案】A ‎【解析】∵且且， ，解得 ‎ ‎∴， 故选：A． ‎ ‎12．【2018陕西西安××区联考】已知函数的值域是，则实数的取值范围是 A. B. C. D. ‎ ‎【答案】C ‎13．【2018黑龙江齐齐哈尔一模】已知函数 ，其中，若对于任意，总存在使得成立，则的最大值为（ ）‎ A. 2 B. C. D. ‎ ‎【答案】C ‎【解析】当0⩽x⩽时,f(x)==−2+∈[−4,−3]，‎ 当0得1