高考数学一轮汇总训练平面向量的概念及其线性运算理新人教A版 14页

‎[备考方向要明了]‎ 考 什 么 怎 么 考 ‎1.了解向量的实际背景．‎ ‎2.理解平面向量的概念，理解两个向量相等的含义．‎ ‎3.理解向量的几何表示．‎ ‎4.掌握向量加法、减法的运算，并理解其几何意义．‎ ‎5.掌握向量数乘的运算及其几何意义，理解两个向量共线的含义．‎ ‎6.了解向量线性运算的性质及其几何意义.‎ ‎1.主要考查平面向量的有关概念及线性运算、共线向量定理的理解和应用，如2012年浙江T5，辽宁T3等．‎ ‎2.考查题型为选择题或填空题.‎ ‎[归纳·知识整合]‎ ‎1．向量的有关概念 名称 定义 向量 既有大小又有方向的量叫做向量，向量的大小叫做向量的长度(或称模)‎ 零向量 长度为零的向量叫做零向量，其方向是任意的，零向量记作0‎ 单位向量 长度等于1个单位的向量 平行向量 方向相同或相反的非零向量叫做平行向量，平行向量又叫共线向量．规定：0与任一向量平行 相等向量 长度相等且方向相同的向量 相反向量 长度相等且方向相反的向量 ‎[探究]　1.两向量共线与平行是两个不同的概念吗？两向量共线是指两向量的方向一致吗？‎ 提示：方向相同或相反的一组非零向量，叫做平行向量，又叫共线向量，是同一个概念．显然两向量平行或共线，其方向可能相同，也可能相反．‎ ‎2．两向量平行与两直线(或线段)平行有何不同？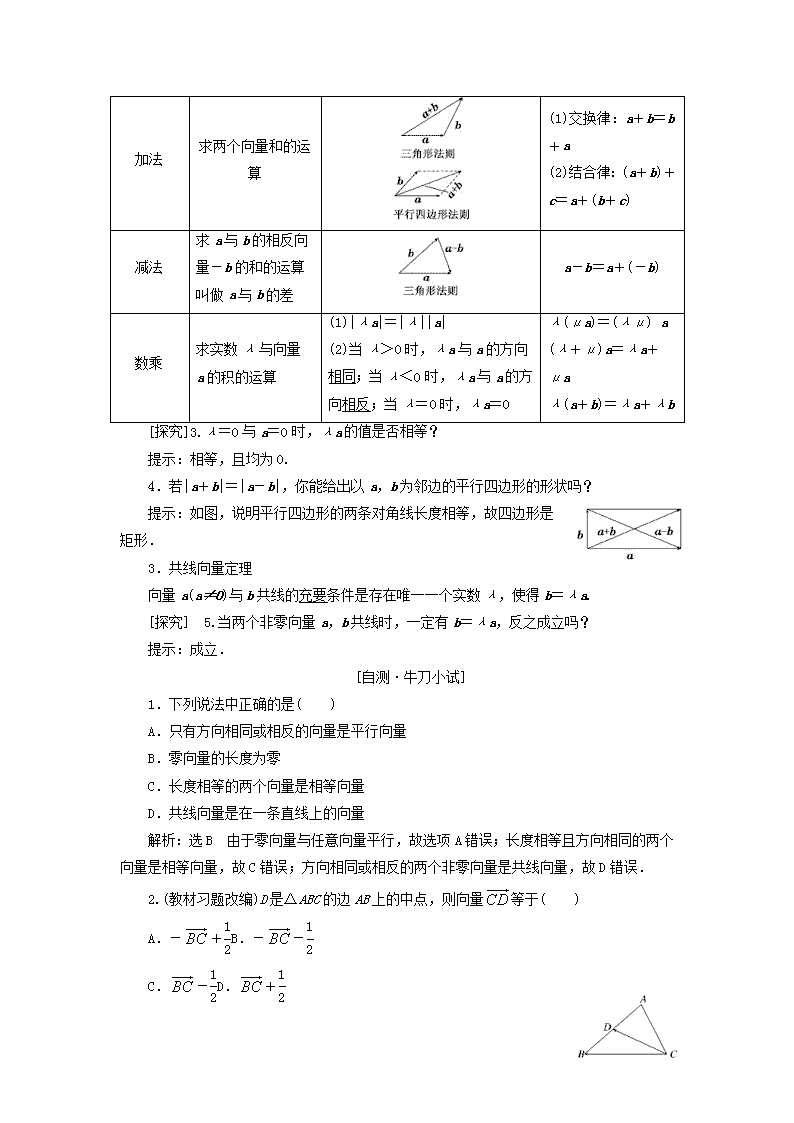‎ 提示：平行向量也叫共线向量，这里的“平行”与两直线(或线段)平行的意义不同，两向量平行时，两向量可以在同一条直线上．‎ ‎2．向量的线性运算 向量运算 定义 法则(或几何意义)‎ 运算律 加法 求两个向量和的运算 ‎(1)交换律：a＋b＝b＋a ‎(2)结合律：(a＋b)＋c＝a＋(b＋c)‎ 减法 求a与b的相反向量－b的和的运算叫做a与b的差 a－b＝a＋(－b)‎ 数乘 求实数λ与向量a的积的运算 ‎(1)|λa|＝|λ||a|‎ ‎(2)当λ＞0时，λa与a的方向相同；当λ＜0时，λa与a的方向相反；当λ＝0时，λa＝0‎ λ(μa)＝(λμ) a ‎(λ＋μ)a＝λa＋μa λ(a＋b)＝λa＋λb ‎[探究]3.λ＝0与a＝0时，λa的值是否相等？‎ 提示：相等，且均为0.‎ ‎4．若|a＋b|＝|a－b|，你能给出以a，b为邻边的平行四边形的形状吗？‎ 提示：如图，说明平行四边形的两条对角线长度相等，故四边形是矩形．‎ ‎3．共线向量定理 向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ，使得b＝λa.‎ ‎[探究]　5.当两个非零向量a，b共线时，一定有b＝λa，反之成立吗？‎ 提示：成立．‎ ‎[自测·牛刀小试]‎ ‎1．下列说法中正确的是(　　)‎ A．只有方向相同或相反的向量是平行向量 B．零向量的长度为零 C．长度相等的两个向量是相等向量 D．共线向量是在一条直线上的向量 解析：选B　由于零向量与任意向量平行，故选项A错误；长度相等且方向相同的两个向量是相等向量，故C错误；方向相同或相反的两个非零向量是共线向量，故D错误．‎ ‎2.(教材习题改编)D是△ABC的边AB上的中点，则向量等于(　　)‎ A．－＋B．－－ C．－D．＋ 解析：选A　如图，由于D是AB的中点，所以＝＋＝＋＝－＋.‎ ‎3．如图，e1，e2为互相垂直的单位向量，则向量a－b可表示为(　　)‎ A．3e2－e1‎ B．－2e1－4e2‎ C．e1－3e2‎ D．3e1－e2‎ 解析：选C　连接a，b的终点，并指向a的终点的向量是a－b.‎ ‎4．(教材习题改编)点C在线段AB上，且＝，则＝________，＝________.‎ 解析：如图，∵＝，∴＝，＝－.‎ 答案：　－ ‎5．(教材习题改编)化简－＋－的结果为______．‎ 解析：－＋－ ‎＝(＋)＋(－)‎ ‎＝＋＝.‎ 答案： 向量的概念 ‎[例1]　给出下列命题：‎ ‎①若|a|＝|b|，则a＝b；‎ ‎②若A，B，C，D是不共线的四点，则＝是四边形ABCD为平行四边形的充要条件；‎ ‎③若a＝b，b＝c，则a＝c；‎ ‎④a＝b的充要条件是|a|＝|b|且a∥b；‎ ‎⑤若a∥b，b∥c，则a∥c.‎ 其中正确命题的序号是(　　)‎ A．②③B．①②‎ C．③④D．④⑤‎ ‎[自主解答]　①不正确，长度相等，但方向不同的向量不是相等向量．‎ ‎②正确．∵＝，∴||＝||且∥，又A，B，C，D是不共线的四点，∴四边形ABCD为平行四边形；反之，若四边形ABCD为平行四边形，则∥且||＝||，因此，＝.‎ ‎③正确．∵a＝b，∴a，b的长度相等且方向相同；‎ 又b＝c，∴b，c的长度相等且方向相同，‎ ‎∴a，c的长度相等且方向相同，故a＝c.‎ ‎④不正确．当a＝－b时，也有|a|＝|b|且a∥b，故|a|＝|b|且a∥b不是a＝b的充要条件，而是必要不充分条件．‎ ‎⑤不正确．未考虑b＝0这种特殊情况．‎ 综上所述，正确命题的序号是②③.‎ ‎[答案]　A ‎———————————————————‎ 解决平面向量概念辨析题的方法 解决与向量概念有关题目的关键是突出向量的核心——方向和长度，如，共线向量的核心是方向相同或相反，长度没有限制；相等向量的核心是方向相同且长度相等；单位向量的核心是方向没有限制，但长度都是一个单位长度；零向量的核心是方向没有限制，长度是0；规定零向量与任意向量共线．只有紧紧抓住概念的核心才能顺利解决与向量概念有关的问题．‎ ‎1．设a0为单位向量，①若a为平面内的某个向量，则a＝|a|a0；②若a与a0平行，则a＝|a|a0；③若a与a0平行且|a|＝1，则a＝a0.上述命题中，假命题的个数是(　　)‎ A．0 B．1‎ C．2 D．3‎ 解析：选D　向量是既有大小又有方向的量，a与|a|a0的模相同，但方向不一定相同，故①是假命题；若a与a0平行，则a与a0的方向有两种情况：一是同向，二是反向，反向时a＝－|a|a0，故②③也是假命题．综上所述，假命题的个数是3.‎ 向量的线性运算 ‎[例2]　在△ABC中，‎ ‎(1)若D是AB边上一点，且＝2，＝＋λ，则λ＝(　　)‎ A.B. C．－D．－ ‎(2)若O是△ABC所在平面内一点，D为BC边中点，且2＋＋＝0，那么(　　)‎ A．＝B．＝2 C．＝3D．2＝ ‎[自主解答]　(1)法一：由＝2得－＝2(－)，即＝＋，所以λ＝.‎ 法二：因为＝＋＝＋＝＋(－)＝＋，所以λ＝.‎ ‎(2)因为D是BC边的中点，所以有＋＝2，所以2＋＋＝2＋2＝2(＋)＝0⇒＋＝0⇒＝.‎ ‎[答案]　(1)A　(2)A 在本例条件下，若||＝||＝|－|＝2，则|＋|为何值？‎ 解：∵||＝||＝|－|，‎ ‎∴△ABC为正三角形．‎ ‎∴|＋|＝2.　　　　‎ ‎———————————————————‎ 平面向量线性运算的一般规律 ‎(1)用已知向量来表示另外一些向量是用向量解题的基本功，除利用向量的加法、减法、数乘运算外，还应充分利用平面几何的一些定理．‎ ‎(2)在求向量时，要尽可能转化到平行四边形或三角形中，运用平行四边形法则、三角形法则，利用三角形中位线、相似三角形对应边成比例等平面几何的性质，把未知向量转化为与已知向量有直接关系的向量来求解．‎ ‎2．如图，在△OAB中，延长BA到C，使AC＝BA，在OB上取点D，使DB＝OB.设＝a，＝b，用a，b表示向量，.‎ 解：＝＋＝＋2＝＋2(－)‎ ‎＝2－＝‎2a－b.‎ ＝－＝－ ‎＝(‎2a－b)－b ‎＝‎2a－b.‎ 共线向量定理的应用 ‎[例3]　设两个非零向量a与b不共线，‎ ‎(1)若＝a＋b，＝‎2a＋8b，＝3(a－b)，求证：A、B、D三点共线．‎ ‎(2)试确定实数k，使ka＋b和a＋kb共线．‎ ‎[自主解答]　(1)∵＝a＋b，＝‎2a＋8b，‎ ＝3(a－b)，‎ ‎∴＝＋＝‎2a＋8b＋3(a－b)，‎ ‎＝‎2a＋8b＋‎3a－3b＝5(a＋b)＝5.‎ ‎∴、共线，又∵它们有公共点B，‎ ‎∴A、B、D三点共线．‎ ‎(2)∵ka＋b与a＋kb共线，‎ ‎∴存在实数λ，使ka＋b＝λ(a＋kb)，‎ 即ka＋b＝λa＋λkb.‎ ‎∴(k－λ)a＝(λk－1)b.‎ ‎∵a、b是不共线的两个非零向量，‎ ‎∴k－λ＝λk－1＝0，∴k2－1＝0，∴k＝±1.‎ ‎———————————————————‎ ‎1．共线向量定理及其应用 ‎(1)可以利用共线向量定理证明向量共线，也可以由向量共线求参数的值．‎ ‎(2)若a，b不共线，则λa＋μb＝0的充要条件是λ＝μ＝0，这一结论结合待定系数法应用非常广泛．‎ ‎2．证明三点共线的方法 若＝λ，则A、B、C三点共线．‎ ‎3．已知a，b不共线，＝a，＝b，＝c，＝d，＝e，设t∈R，如果‎3a＝c,2b＝d，e＝t(a＋b)，是否存在实数t使C，D，E三点在一条直线上？若存在，求出实数t的值，若不存在，请说明理由．‎ 解：由题设知，＝d－c＝2b－‎3a，＝e－c＝(t－3)a＋tb，C，D，E 三点在一条直线上的充要条件是存在实数k，使得＝k，即(t－3)a＋tb＝－3ka＋2kb，‎ 整理得(t－3＋3k)a＝(2k－t)b.‎ 因为a，b不共线，所以有 解之得t＝.‎ 故存在实数t＝使C，D，E三点在一条直线上．‎ 1个规律——向量加法规律 一般地，首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量，即＋＋＋…＋＝.特别地，一个封闭图形首尾连接而成的向量和为零向量．‎ 2个结论——向量的中线公式及三角形的重心 ‎(1)向量的中线公式 若P为线段AB的中点，O为平面内一点，则＝(＋)．‎ ‎(2)三角形的重心 已知平面内不共线的三点A、B、C，＝(＋＋)⇔G是△ABC的重心，特别地，＋＋＝0⇔P为△ABC的重心．‎ 3个等价转化——与三点共线有关的等价转化 A，P，B三点共线⇔＝λ (λ≠0)⇔＝(1－t)·＋t (O为平面内异于A，P，B的任一点，t∈R)⇔＝x＋y (O为平面内异于A，P，B的任一点，x∈R，y∈R，x＋y＝1)．‎ 4个注意点——向量线性运算应注意的问题 ‎(1)用平行四边形法则进行向量加法和减法运算时，需将向量平移至共起点；‎ ‎(2)作两个向量的差时，要注意向量的方向是指向被减向量的终点；‎ ‎(3)在向量共线的重要条件中要注意“a≠‎0”‎，否则λ可能不存在，也可能有无数个；‎ ‎(4)要注意向量共线与三点共线的区别与联系. ‎ 创新交汇——以平面向量为背景的新定义问题 ‎1．从近几年新课标省份的高考可以看出，高考以新定义的形式考查向量的概念及线性运算的频率较大，且常与平面几何、解析几何、充要条件等知识交汇，具有考查形式灵活，题材新颖，解法多样等特点．‎ ‎2．解决此类问题，首先需要分析新定义的特点，把新定义所叙述的问题的本质弄清楚，通过转化思想解决，这是破解新定义信息题难点的关键所在．‎ ‎[典例]　(2011·山东高考)设A1，A2，A3，A4是平面直角坐标系中两两不同的四点，若＝λ(λ∈R)，＝μ (μ∈R)，且＋＝2，则称A3，A4调和分割A1，A2·已知点C(c,0)，D(d,0)(c，d∈R)调和分割点A(0,0)，B(1,0)，则下面说法正确的是(　　)‎ A．C可能是线段AB的中点 B．D可能是线段AB的中点 C．C，D可能同时在线段AB上 D．C，D不可能同时在线段AB的延长线上 ‎[解析]　根据已知得(c,0)－(0,0)＝λ[(1,0)－(0,0)]，即(c,0)＝λ(1,0)，从而得c＝λ；(d,0)－(0,0)＝μ[(1,0)－(0,0)]，即(d,0)＝μ(1,0)，得d＝μ.根据＋＝2，得＋＝2.线段AB的方程是y＝0，x∈[0,1]．若C是线段AB的中点，则c＝，代入＋＝2得，＝0，此等式不可能成立，故选项A的说法不正确；同理选项B的说法也不正确；若C，D同时在线段AB上，则01，d>1，则＋<2，与＋＝2矛盾，若c<0，d<0，则＋是负值，与＋＝2矛盾，若c>1，d<0，则<1，<0，此时＋<1，与＋＝2矛盾；故选项D的说法是正确的．‎ ‎[答案]　D ‎1．本题具有以下创新点 ‎(1)命题背景新颖：本题为新定义题目，用新定义考查考生阅读能力与知识迁移能力．‎ ‎(2)考查知识新颖：本题把坐标系、向量、点与线段的位置关系通过新定义有机结合在一起，能较好地考查学生的阅读理解能力和解决问题的能力．‎ ‎2．解决本题的关键有以下两点 解决本题的关键是抓住两条：一是A1，A2，A3，A4四点共线；二是＋＝2，同时应用排除法．‎ ‎1．定义平面向量之间的一种运算“⊙”如下：对任意的a＝(m，n)，b＝(p，q)，令a⊙b＝mq－np，下面说法错误的是(　　)‎ A．若a与b共线，则a⊙b＝0‎ B．a⊙b＝b⊙a C．对任意的λ∈R，有(λa)⊙b＝λ(a⊙b)‎ D．(a⊙b)2＋(a·b)2＝|a|2|b|2‎ 解析：选B　若a与b共线，则有mq－np＝0，故A正确；因为b⊙a＝pn－qm，而a⊙b＝mq－np，所以有a⊙b≠b⊙a，故B错误；因为λa＝(λm，λn)，所以(λa)⊙b＝λmq－λnp.又λ(a⊙b)＝λ(mq－np)＝(λa)⊙b，故C正确；因为(a⊙b)2＋(a·b)2＝(mq－np)2＋(mp＋nq)2＝(m2＋n2)(p2＋q2)＝|a|2|b|2，故D正确．‎ ‎2．已知点A、B、C是直线l上不同的三个点，点O不在直线l上，则关于x的方程x2＋x＋＝0的解集为(　　)‎ A．∅B．{－1}‎ C.D．{－1,0}‎ 解析：选A　由条件可知，x2＋x不能和共线，即使x＝0时，也不满足条件，所以满足条件的x不存在．‎ 一、选择题(本大题共6小题，每小题5分，共30分)‎ ‎1.如图，已知＝a，＝b，＝3，用a，b表示，则＝(　　)‎ A．a＋bB.a＋b C.a＋bD.a＋b 解析：选B　∵＝－＝a－b，又＝3，‎ ‎∴＝＝(a－b)，∴＝＋＝b＋(a－b)＝a＋b.‎ ‎2．设P是△ABC所在平面内的一点，＋＝2，则(　　)‎ A．＋＝0　　　　　　　B．＋＝0‎ C．＋＝0 D．＋＋＝0‎ 解析：选B　如图，根据向量加法的几何意义，＋＝2⇔P是AC的中点，故＋＝0.‎ ‎3．已知向量p＝＋，其中a、b均为非零向量，则|p|的取值范围是(　　)‎ A．[0，] B．[0,1]‎ C．(0,2] D．[0,2]‎ 解析：选D　与均为单位向量，当它们同向时，|p|取得最值2，当它们反向时，|p|取得最小值0.故|p|∈[0,2]．‎ ‎4．已知四边形ABCD中，＝，||＝||，则这个四边形的形状是(　　)‎ A．平行四边形 B．矩形 C．等腰梯形 D．菱形 解析：选B　由＝可知AB綊CD，所以四边形ABCD为平行四边形．由||＝||知对角线相等，所以平行四边形ABCD为矩形．‎ ‎5．(2013·保定模拟)如图所示，已知点G是△ABC的重心，过G作直线与AB，AC两边分别交于M，N两点，且＝x，＝y，则的值为(　　)‎ A．3 B. C．2 D. 解析：选B　(特例法)利用等边三角形，过重心作平行于底面BC的直线，易得＝.‎ ‎6．设D、E、F分别是△ABC的三边BC、CA、AB上的点，且＝2，＝2，＝2，则＋＋与 (　　)‎ A．反向平行　　　　　　　B．同向平行 C．互相垂直 D．既不平行也不垂直 解析：选A　由题意得＝＋＝＋，‎ ＝＋＝＋，‎ ＝＋＝＋，‎ 因此＋＋＝＋(＋－)‎ ‎＝＋＝－，‎ 故＋＋与反向平行．‎ 二、填空题(本大题共3小题，每小题5分，共15分)‎ ‎7．在▱ABCD中，＝a，＝b，＝3，M为BC的中点，则＝________(用a，b表示)．‎ 解析：由＝3得4＝3＝3(a＋b)，‎ ＝a＋b，‎ 所以＝(a＋b)－＝－a＋b.‎ 答案：－a＋b ‎8．设a，b是两个不共线的非零向量，若‎8a＋kb与ka＋2b共线，则实数k＝________.‎ 解析：因为‎8a＋kb与ka＋2b共线，所以存在实数λ，使‎8a＋kb＝λ(ka＋2b)，即(8－λk)a＋(k－2λ)b＝0.又a，b是两个不共线的非零向量，故解得k＝±4.‎ 答案：±4‎ ‎9．(2013·淮阴模拟)已知△ABC和点M满足＋＋＝0.若存在实数m使得＋＝m成立，则m＝________.‎ 解析：由题目条件可知，M为△ABC的重心，连接AM并延长交BC于D，则＝，因为AD为中线，则＋＝2＝3，所以m＝3.‎ 答案：3‎ 三、解答题(本大题共3小题，每小题12分，共36分)‎ ‎10．已知P为△ABC内一点，且3＋4＋5＝0，延长AP交BC于点D，若＝a，＝b，用a、b表示向量，.‎ 解：∵＝－＝－a，‎ ＝－＝－b，‎ 又3＋4＋5＝0.‎ ‎∴3＋4(－a)＋5(－b)＝0，∴＝a＋b.‎ 设＝t (t∈R)，‎ 则＝ta＋tb.①‎ 又设＝k (k∈R)，‎ 由＝－＝b－a，得＝k(b－a)．‎ 而＝＋＝a＋.‎ ‎∴＝a＋k(b－a)＝(1－k)a＋kb②‎ 由①②得解得t＝.‎ 代入①得＝a＋b.‎ ‎∴＝a＋b，＝a＋b.‎ ‎11．设两个非零向量e1和e2不共线．‎ ‎(1)如果＝e1－e2，＝3e1＋2e2，＝－8e1－2e2，‎ 求证：A、C、D三点共线；‎ ‎(2)如果＝e1＋e2，＝2e1－3e2，＝2e1－ke2，且A、C、D三点共线，求k的值．‎ 解：(1)证明：∵＝e1－e2，＝3e1＋2e2，‎ ＝－8e1－2e2，‎ ‎∴＝＋＝4e1＋e2‎ ‎＝－(－8e1－2e2)＝－，‎ ‎∴与共线．‎ 又∵与有公共点C，∴A、C、D三点共线．‎ ‎(2) ＝＋＝(e1＋e2)＋(2e1－3e2)＝3e1－2e2，‎ ‎∵A、C、D三点共线，∴与共线，从而存在实数λ使得＝λ，即3e1－2e2＝λ(2e1－ke2)，得 解得λ＝，k＝.‎ ‎12．设点O在△ABC内部，且有4＋＋＝0，求△ABC的面积与△OBC的面积之比．‎ 解：取BC的中点D，连接OD，‎ 则＋＝2，‎ 又4＝－(＋)＝－2，‎ 即＝－，‎ ‎∴O、A、D三点共线，且||＝2||，‎ ‎∴O是中线AD上靠近A点的一个三等分点，‎ ‎∴S△ABC∶S△OBC＝3∶2.‎ ‎1．已知△ABC的三个顶点A、B、C及平面内一点P满足＋＋＝，则点P与△ABC的关系为(　　)‎ A．P在△ABC内部 B．P在△ABC外部 C．P在AB边所在直线上 D．P是AC边的一个三等分点 解析：选D　∵＋＋＝，‎ ‎∴＋＋＝－，∴＝－2＝2，‎ ‎∴P是AC边的一个三等分点．‎ ‎2．平面向量a，b共线的充要条件是(　　)‎ A．a，b方向相同 B．a，b两向量中至少有一个为0‎ C．存在λ∈R，使b＝λa D．存在不全为零的实数λ1，λ2，使λ‎1a＋λ2b＝0‎ 解析：选D　a，b共线时，a，b方向相同或相反，故A错．a，b共线时，a，b不一定是零向量，故B错．当b＝λa时，a，b一定共线，若b≠0，a＝0，则b＝λa不成立，故C错．排除A、B、C.‎ ‎3．△ABC中，点D在边AB上，CD平分∠ACB.设＝a，＝b，|a|＝1，|b|＝2，则等于(　　)‎ A.a＋bB.a＋b C.a＋bD.a＋b 解析：选B　∵CD平分∠ACB，‎ ‎∴＝.‎ 又∵＝a，＝b，|a|＝1，|b|＝2，‎ ‎∴＝.‎ ‎∴＝＋＝a＋ ‎＝a＋(－)‎ ‎＝a＋(b－a)＝a＋b.‎ ‎4.如图所示，在五边形ABCDE中，点M、N、P、Q分别是AB、CD、BC、DE的中点，K和L分别是MN和PQ的中点，求证：＝.‎ 证明：任取一点O，＝－.‎ ‎∵K、L为MN、PQ的中点．‎ ‎∴＝(＋)，＝(＋)．‎ 又∵M，N，P，Q分别为AB，CD，BC，DE中点，‎ ‎∴＝(＋)，＝(＋)，‎ ＝(＋)，＝(＋)．‎ ‎∴＝－＝[－(＋)＋(＋)]‎ ‎＝[－(＋＋＋)＋(＋＋＋)]‎ ‎＝(－＋)＝.‎