天津理科高考试题含解析 12页

‎2013年普通高等学校夏季招生全国统一考试数学理工农医类 ‎(天津卷)‎ 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试用时120分钟．第Ⅰ卷1至2页，第Ⅱ卷3至5页．‎ 答卷前，考生务必将自己的姓名、准考号填写在答题卡上，并在规定位置粘贴考试用条形码．答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效．考试结束后，将本试卷和答题卡一并交回．‎ 祝各位考生考试顺利！‎ 第Ⅰ卷 注意事项：‎ ‎1．每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．‎ ‎2．本卷共8小题，每小题5分，共40分．‎ 参考公式：‎ ‎·如果事件A，B互斥，那么P(A∪B)＝P(A)＋P(B)．‎ ‎·如果事件A，B相互独立，那么P(AB)＝P(A)P(B)．‎ ‎·棱柱的体积公式V＝Sh.其中S表示棱柱的底面面积，h表示棱柱的高．‎ ‎·球的体积公式V＝.其中R表示球的半径．‎ 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．(2013天津，理1)已知集合A＝{x∈R||x|≤2}，B＝{x∈R|x≤1}，则A∩B＝(　　)．‎ A．(－∞，2] B．[1,2]‎ C．[－2,2] D．[－2,1]‎ 答案：D 解析：解不等式|x|≤2，得－2≤x≤2，所以A＝{x|－2≤x≤2}，所以A∩B＝{x|－2≤x≤1}．故选D.‎ ‎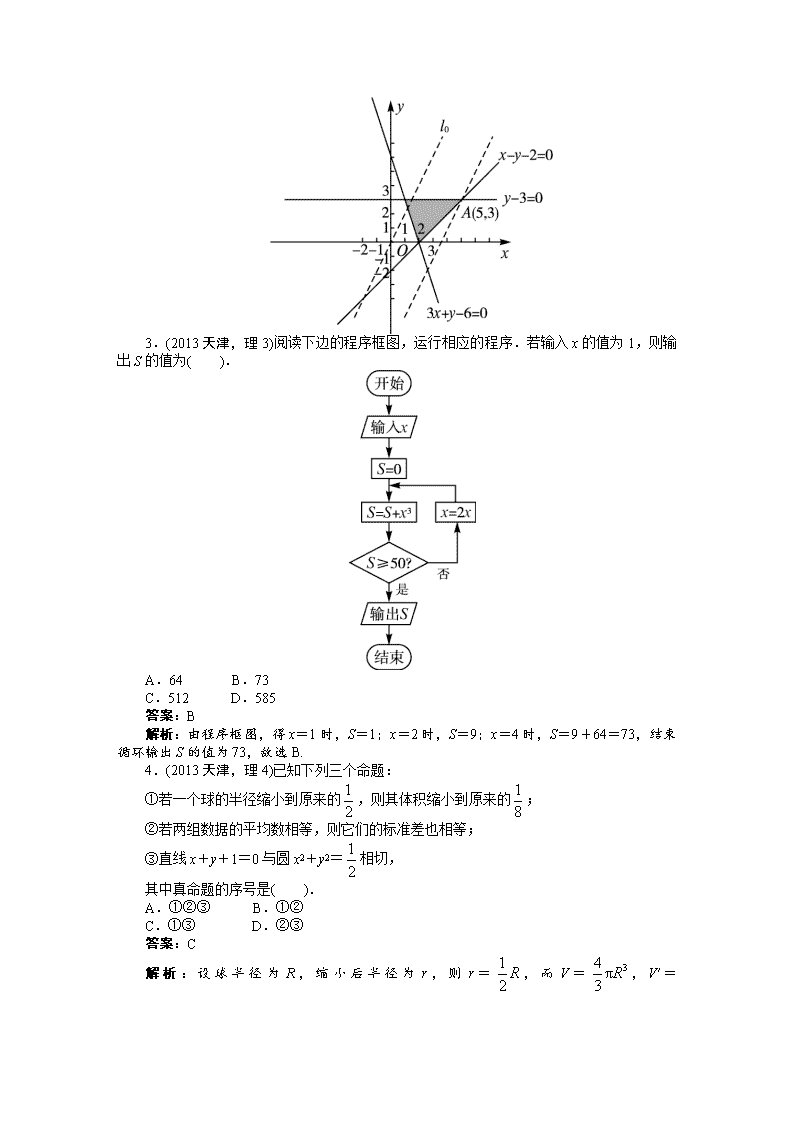2．(2013天津，理2)设变量x，y满足约束条件则目标函数z＝y－2x的最小值为(　　)．‎ A．－7 B．－4‎ C．1 D．2‎ 答案：A 解析：作约束条件所表示的可行区域，如图所示，z＝y－2x可化为y＝2x＋z，z表示直线在y轴上的截距，截距越大z越大，作直线l0：y＝2x，平移l0过点A(5,3)，此时z最小为－7，故选A.‎ ‎3．(2013天津，理3)阅读下边的程序框图，运行相应的程序．若输入x的值为1，则输出S的值为(　　)．‎ A．64 B．73‎ C．512 D．585‎ 答案：B 解析：由程序框图，得x＝1时，S＝1；x＝2时，S＝9；x＝4时，S＝9＋64＝73，结束循环输出S的值为73，故选B.‎ ‎4．(2013天津，理4)已知下列三个命题：‎ ‎①若一个球的半径缩小到原来的，则其体积缩小到原来的；‎ ‎②若两组数据的平均数相等，则它们的标准差也相等；‎ ‎③直线x＋y＋1＝0与圆x2＋y2＝相切，‎ 其中真命题的序号是(　　)．‎ A．①②③ B．①②‎ C．①③ D．②③‎ 答案：C 解析：设球半径为R，缩小后半径为r，则r＝，而V＝，V′＝‎ ‎，所以该球体积缩小到原来的，故①为真命题；两组数据的平均数相等，它们的方差可能不相等，故②为假命题；圆x2＋y2＝的圆心到直线x＋y＋1＝0的距离d＝，因为该距离等于圆的半径，所以直线与圆相切，故③为真命题．故选C.‎ ‎5．(2013天津，理5)已知双曲线(a＞0，b＞0)的两条渐近线与抛物线y2＝2px(p＞0)的准线分别交于A，B两点，O为坐标原点．若双曲线的离心率为2，△AOB的面积为，则p＝(　　)．‎ A．1 B． C．2 D．3‎ 答案：C 解析：设A点坐标为(x0，y0)，则由题意，得S△AOB＝|x0|·|y0|＝.抛物线y2＝2px的准线为，所以，代入双曲线的渐近线的方程，得|y0|＝.由得b＝，所以|y0|＝.所以S△AOB＝，解得p＝2或p＝－2(舍去)．‎ ‎6．(2013天津，理6)在△ABC中，∠ABC＝，AB＝，BC＝3，则sin∠BAC＝(　　)．‎ A． B．‎ C． D．‎ 答案：C 解析：在△ABC中，由余弦定理得AC2＝AB2＋BC2－2AB·BCcos∠ABC＝＝5，即得AC＝.由正弦定理，即，所以sin∠BAC＝.‎ ‎7．(2013天津，理7)函数f(x)＝2x|log0.5x|－1的零点个数为(　　)．‎ A．1 B．‎2 C．3 D．4‎ 答案：B 解析：函数f(x)＝2x|log0.5x|－1的零点也就是方程2x|log0.5x|－1＝0的根，即2x|log0.5x|＝1，整理得|log0.5x|＝.令g(x)＝|log0.5x|，h(x)＝，作g(x)，h(x)的图象如图所示．因为两个函数图象有两个交点，所以f(x)有两个零点．‎ ‎8．(2013天津，理8)已知函数f(x)＝x(1＋a|x|)．设关于x的不等式f(x＋a)＜f(x)的解集为A.若A，则实数a的取值范围是(　　)．‎ A． B．‎ C． D．‎ 答案：A 解析：f(x)＝x(1＋a|x|)＝‎ 若不等式f(x＋a)＜f(x)的解集为A，且，‎ 则在区间上，函数y＝f(x＋a)的图象应在函数y＝f(x)的图象的下边．‎ ‎(1)当a＝0时，显然不符合条件．‎ ‎(2)当a＞0时，画出函数y＝f(x)和y＝f(x＋a)的图象大致如图．‎ 由图可知，当a＞0时，y＝f(x＋a)的图象在y＝f(x)图象的上边，故a＞0不符合条件．‎ ‎(3)当a＜0时，画出函数y＝f(x)和y＝f(x＋a)的图象大致如图．‎ 由图可知，若f(x＋a)＜f(x)的解集为A，且，‎ 只需即可，‎ 则有(a＜0)，‎ 整理，得a2－a－1＜0，解得.‎ ‎∵a＜0，∴a∈.‎ 综上，可得a的取值范围是.‎ 第Ⅱ卷 注意事项：‎ ‎1．用黑色墨水的钢笔或签字笔将答案写在答题卡上．‎ ‎2．本卷共12小题，共110分．‎ 二、填空题：本大题共6小题，每小题5分，共30分．‎ ‎9．(2013天津，理9)已知a，b∈R，i是虚数单位．若(a＋i)·(1＋i)＝bi，则a＋bi＝__________.‎ 答案：1＋2i 解析：由(a＋i)(1＋i)＝a－1＋(a＋1)i＝bi，得解方程组，得a＝1，b＝2，则a＋bi＝1＋2i.‎ ‎10．(2013天津，理10)的二项展开式中的常数项为__________．‎ 答案：15‎ 解析：二项展开式的通项为，得r＝4，所以二项展开式的常数项为T5＝(－1)4＝15.‎ ‎11．(2013天津，理11)已知圆的极坐标方程为ρ＝4cos θ，圆心为C，点P的极坐标为，则|CP|＝__________.‎ 答案：‎ 解析：由圆的极坐标方程为ρ＝4cos θ，得圆心C的直角坐标为(2,0)，点P的直角坐标为(2,)，所以|CP|＝.‎ ‎12．(2013天津，理12)在平行四边形ABCD中，AD＝1，∠BAD＝60°，E为CD的中点．若·＝1，则AB的长为__________．‎ 答案：‎ 解析：如图所示，在平行四边形ABCD中，＝＋，＝＋＝＋.‎ 所以·＝(＋)·＝||2＋||2＋·＝||2＋||＋1＝1，解方程得||＝(舍去||＝0)，所以线段AB的长为.‎ ‎13．(2013天津，理13)如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC.过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F.若AB＝AC，AE＝6，BD＝5，则线段CF的长为__________．‎ 答案：‎ 解析：∵AE为圆的切线，‎ ‎∴由切割线定理，得AE2＝EB·ED.‎ 又AE＝6，BD＝5，可解得EB＝4.‎ ‎∵∠EAB为弦切角，且AB＝AC，‎ ‎∴∠EAB＝∠ACB＝∠ABC.‎ ‎∴EA∥BC.又BD∥AC，‎ ‎∴四边形EBCA为平行四边形．‎ ‎∴BC＝AE＝6，AC＝EB＝4.‎ 由BD∥AC，得△ACF∽△DBF，‎ ‎∴.‎ 又CF＋BF＝BC＝6，∴CF＝.‎ ‎14．(2013天津，理14)设a＋b＝2，b＞0，则当a＝__________时，取得最小值．‎ 答案：－2‎ 解析：因为a＋b＝2，所以 ‎1＝＝‎ ‎≥，‎ 当a＞0时，，；‎ 当a＜0时，，，当且仅当b＝2|a|时等号成立．‎ 因为b＞0，所以原式取最小值时b＝－‎2a.‎ 又a＋b＝2，所以a＝－2时，原式取得最小值．‎ 三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．‎ ‎15．(2013天津，理15)(本小题满分13分)已知函数f(x)＝＋6sin xcos x－2cos2x＋1，x∈R.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)求f(x)在区间上的最大值和最小值．‎ 解：(1)f(x)＝sin 2x·＋3sin 2x－cos 2x ‎＝2sin 2x－2cos 2x＝.‎ 所以，f(x)的最小正周期T＝＝π.‎ ‎(2)因为f(x)在区间上是增函数，在区间上是减函数．又f(0)＝－2，，，故函数f(x)在区间上的最大值为，最小值为－2.‎ ‎16．(2013天津，理16)(本小题满分13分)一个盒子里装有7张卡片，其中有红色卡片4张，编号分别为1,2,3,4；白色卡片3张，编号分别为2,3,4.从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同)．‎ ‎(1)求取出的4张卡片中，含有编号为3的卡片的概率；‎ ‎(2)在取出的4张卡片中，红色卡片编号的最大值设为X，求随机变量X的分布列和数学期望．‎ 解：(1)设“取出的4张卡片中，含有编号为3的卡片”为事件A，则 P(A)＝.‎ 所以，取出的4张卡片中，含有编号为3的卡片的概率为.‎ ‎(2)随机变量X的所有可能取值为1,2,3,4.‎ P(X＝1)＝，‎ P(X＝2)＝，‎ P(X＝3)＝，‎ P(X＝4)＝.‎ 所以随机变量X的分布列是 X ‎1‎ ‎2‎ ‎3‎ ‎4‎ P 随机变量X的数学期望EX＝1×＋2×＋3×＋4×＝.‎ ‎17．(2013天津，理17)(本小题满分13分)如图，四棱柱ABCD－A1B‎1C1D1中，侧棱A‎1A⊥底面ABCD，AB∥DC，AB⊥AD，AD＝CD＝1，AA1＝AB＝2，E为棱AA1的中点．‎ ‎(1)证明B‎1C1⊥CE；‎ ‎(2)求二面角B1－CE－C1的正弦值；‎ ‎(3)设点M在线段C1E上，且直线AM与平面ADD‎1A1所成角的正弦值为，求线段AM的长．‎ 解：(方法一)‎ ‎(1)证明：如图，以点A为原点建立空间直角坐标系，依题意得A(0,0,0)，B(0,0,2)，C(1,0,1)，B1(0,2,2)，C1(1,2,1)，E(0,1,0)．‎ 易得＝(1,0，－1)，＝(－1,1，－1)，于是·＝0，‎ 所以B‎1C1⊥CE.‎ ‎(2)＝(1，－2，－1)．‎ 设平面B1CE的法向量m＝(x，y，z)，‎ 则即 消去x，得y＋2z＝0，不妨令z＝1，可得一个法向量为m＝(－3，－2,1)．‎ 由(1)，B‎1C1⊥CE，又CC1⊥B‎1C1，可得B‎1C1⊥平面CEC1，‎ 故＝(1,0，－1)为平面CEC1的一个法向量．‎ 于是cos〈m，〉＝，‎ 从而sin〈m，〉＝.‎ 所以二面角B1－CE－C1的正弦值为.‎ ‎(3)＝(0,1,0)，＝(1,1,1)．‎ 设＝λ＝(λ，λ，λ)，0≤λ≤1，有＝＋＝(λ，λ＋1，λ)．‎ 可取＝(0,0,2)为平面ADD‎1A1的一个法向量．‎ 设θ为直线AM与平面ADD‎1A1所成的角，则 sin θ＝|cos〈，〉|＝‎ ‎＝.‎ 于是，解得，‎ 所以AM＝.‎ ‎(方法二)‎ ‎ (1)证明：因为侧棱CC1⊥底面A1B‎1C1D1，B‎1C1平面A1B‎1C1D1，‎ 所以CC1⊥B‎1C1.‎ 经计算可得B1E＝，B‎1C1＝，EC1＝，‎ 从而B1E2＝，‎ 所以在△B1EC1中，B‎1C1⊥C1E，‎ 又CC1，C1E平面CC1E，CC1∩C1E＝C1，‎ 所以B‎1C1⊥平面CC1E，‎ 又CE平面CC1E，故B‎1C1⊥CE.‎ ‎(2)过B1作B‎1G⊥CE于点G，连接C‎1G.‎ 由(1)，B‎1C1⊥CE，故CE⊥平面B‎1C1G，得CE⊥C‎1G，‎ 所以∠B1GC1为二面角B1－CE－C1的平面角．‎ 在△CC1E中，由CE＝C1E＝，CC1＝2，可得C‎1G＝.‎ 在Rt△B‎1C1G中，B‎1G＝，‎ 所以sin∠B1GC1＝，‎ 即二面角B1－CE－C1的正弦值为.‎ ‎(3)连接D1E，过点M作MH⊥ED1于点H，可得MH⊥平面ADD‎1A1，连接AH，AM，则∠MAH为直线AM与平面ADD‎1A1所成的角．‎ 设AM＝x，从而在Rt△AHM中，有MH＝，AH＝.‎ 在Rt△C1D1E中，C1D1＝1，ED1＝，得EH＝.‎ 在△AEH中，∠AEH＝135°，AE＝1，‎ 由AH2＝AE2＋EH2－2AE·EHcos 135°，得，‎ 整理得5x2－－6＝0，解得x＝.‎ 所以线段AM的长为.‎ ‎18．(2013天津，理18)(本小题满分13分)设椭圆(a＞b＞0)的左焦点为F，离心率为，过点F且与x轴垂直的直线被椭圆截得的线段长为.‎ ‎(1)求椭圆的方程；‎ ‎(2)设A，B分别为椭圆的左、右顶点，过点F且斜率为k的直线与椭圆交于C，D两点．若·＋·＝8，求k的值．‎ 解：(1)设F(－c,0)，由，知.过点F且与x轴垂直的直线为x＝－c，代入椭圆方程有，‎ 解得，于是，解得，‎ 又a2－c2＝b2，从而a＝，c＝1，‎ 所以椭圆的方程为.‎ ‎(2)设点C(x1，y1)，D(x2，y2)，由F(－1,0)得直线CD的方程为y＝k(x＋1)，‎ 由方程组消去y，整理得(2＋3k2)x2＋6k2x＋3k2－6＝0.‎ 求解可得x1＋x2＝，x1x2＝.‎ 因为A(，0)，B(，0)，‎ 所以·＋·‎ ‎＝(x1＋，y1)·(－x2，－y2)＋(x2＋，y2)·(－x1，－y1)‎ ‎＝6－2x1x2－2y1y2＝6－2x1x2－2k2(x1＋1)(x2＋1)‎ ‎＝6－(2＋2k2)x1x2－2k2(x1＋x2)－2k2‎ ‎＝.‎ 由已知得＝8，解得k＝.‎ ‎19．(2013天津，理19)(本小题满分14分)已知首项为的等比数列{an}不是递减数列，其前n项和为Sn(n∈N*)，且S3＋a3，S5＋a5，S4＋a4成等差数列．‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)设Tn＝(n∈N*)，求数列{Tn}的最大项的值与最小项的值．‎ 解：(1)设等比数列{an}的公比为q，‎ 因为S3＋a3，S5＋a5，S4＋a4成等差数列，‎ 所以S5＋a5－S3－a3＝S4＋a4－S5－a5，‎ 即‎4a5＝a3，于是.‎ 又{an}不是递减数列且，所以.‎ 故等比数列{an}的通项公式为.‎ ‎(2)由(1)得 当n为奇数时，Sn随n的增大而减小，所以1＜Sn≤S1＝，‎ 故.‎ 当n为偶数时，Sn随n的增大而增大，所以＝S2≤Sn＜1，‎ 故.‎ 综上，对于n∈N*，总有.‎ 所以数列{Tn}最大项的值为，最小项的值为.‎ ‎20．(2013天津，理20)(本小题满分14分)已知函数f(x)＝x2ln x.‎ ‎(1)求函数f(x)的单调区间；‎ ‎(2)证明：对任意的t＞0，存在唯一的s，使t＝f(s)；‎ ‎(3)设(2)中所确定的s关于t的函数为s＝g(t)，证明：当t＞e2时，有.‎ 解：(1)函数f(x)的定义域为(0，＋∞)．‎ f′(x)＝2xln x＋x＝x(2ln x＋1)，令f′(x)＝0，得.‎ 当x变化时，f′(x)，f(x)的变化情况如下表：‎ x f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎  极小值 所以函数f(x)的单调递减区间是，单调递增区间是.‎ ‎(2)证明：当0＜x≤1时，f(x)≤0.‎ 设t＞0，令h(x)＝f(x)－t，x∈[1，＋∞)．‎ 由(1)知，h(x)在区间(1，＋∞)内单调递增．‎ h(1)＝－t＜0，h(et)＝e2tln et－t＝t(e2t－1)＞0.‎ 故存在唯一的s∈(1，＋∞)，使得t＝f(s)成立．‎ ‎(3)证明：因为s＝g(t)，由(2)知，t＝f(s)，且s＞1，从而 ‎，‎ 其中u＝ln s.‎ 要使成立，只需.‎ 当t＞e2时，若s＝g(t)≤e，则由f(s)的单调性，有t＝f(s)≤f(e)＝e2，矛盾．‎ 所以s＞e，即u＞1，从而ln u＞0成立．‎ 另一方面，令F(u)＝，u＞1.F′(u)＝，令F′(u)＝0，得u＝2.‎ 当1＜u＜2时，F′(u)＞0；当u＞2时，F′(u)＜0.‎ 故对u＞1，F(u)≤F(2)＜0.‎ 因此成立．‎ 综上，当t＞e2时，有.‎