海壁普通高等学校招生全国统一考试高考仿真模拟信息卷押题卷文科数学十 5页

海壁：2019年普通高等学校招生全国统一考试高考仿真模拟信息卷&押题卷 文科数学（十）‎ 数 学 ‎（考试时间：120分钟 满分：120分）‎ 一、 选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。‎ 1. 全集U={x∣x>-1}，集合A={x∣y=}，则CuA=（ ）‎ A. ‎( -1,0 ] B.( -1,0 ) C. ( -1,3 ] D. B.( -1,3 ) ‎ 2. ‎（ ）‎ A. ‎ B. C. D. ‎ 3. 已知平面向量a=（2,1），b=（-3,λ），若（a+2b）⊥a，则实数λ的值为（ ）‎ A. ‎ B. C. D. ‎ ‎4. 若tan（α+β）=，tanβ=，则tanα=（ ）‎ A. B. C. D. ‎ ‎5. 将甲同学10次数学测试的成绩统计如图所示，则甲同学这10次成绩的中位数与平均数分别为（ ）‎ ‎ A. 99，93.6 B. 95.5，93.6 C. 92，93.6 D. 95.5,93.7‎ ‎6. 已知左、右交点分别为F1，F2的双曲线C：过点（，），点P在双曲线C上，若∠F1PF2=60°，则 ‎∣PF1∣·∣PF2∣=（ ）‎ ‎ A. 3 B. 6 C. 4 D. 8‎ ‎7. 已知函数ƒ（x）是定义在R上的偶函数，且当x≥0时，ƒ（x）=2x3-3x，则曲线y=ƒ（x）在（-2，ƒ（-2））处的切线方程为（ ）‎ ‎ A. 15x+y+20=0 B. 15x-y+40=0 C. 21x-y+52=0 D. 21x+y+32=0‎ ‎8. 已知等差数列{an}的前n项和为Sn，且S10=60，a7=9，等比数列{bn}的前n项积为Tn，且T14=128，则S20+b7b8=（ ）‎ ‎ A. 297 B.322 C. 312 D. 287‎ 9. ‎ 下图网络格纸中小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（ ）‎ A. ‎80+12π B. 80-4π C. 80+4π D. 80+8π 9. 已知函数ƒ（x）=2sin（-3x），则下列说法中，错误的是（ ）‎ A. x=是函数ƒ（x）的图像的一条对称轴 ‎ B. 函数ƒ（x）的单调递增区间为[+++]（k∈Z）‎ C. 将函数ƒ（x）的图像向左平移个单位后，关于y轴对称 D. 函数ƒ（x）在[，π]上的值域为[，]‎ 10. ‎ 已知∆ABC的面积为15，角A，B，C的对边分别为a，b，c，若b=14，（a+2c）cosB+bcosA=0，则a+c=‎ A. 16 B. 12 C. 8 D. 4‎ 11. ‎ 若关于x的不等式2x3+ax2>lnx2在（0，+∞）上恒成立，则实数a的取值范围为 A. [ -2，+∞) B. ( -2，+∞) C. [ -1，+∞) D. ( -1，+∞) ‎ 一、 填空题：本大题共4小题，每小题5分，共20分。‎ 13. ‎ 已知定义在R上的奇函数ƒ（x）满足，当x>0时，ƒ（x）=x3-cos x，则当x<0时，ƒ（x） .‎ 14. ‎ 已知实数x，y满足，则z=5x-y的最大值为 .‎ 15. 拿破仑为人颇为好学，是法兰西科学院院士，他对数学方面很感兴趣，自幼喜爱数学，他在行军打仗的空闲时间，经常研究平面几何。他提出了拿破仑定理：若在任意三角形各边向外(内)作正三角形，则它们的中心构成一个正三角形。如图所示，以等边∆GEI的三条边为边，向外作3个正三角形，取它们的中心A，B，C，顺次连接，得到∆ABC，图中阴影部分为∆GEI与∆ABC的公共部分。若往∆DFH中投掷一点，则该点落在阴影部分内的概率为 .‎ 16. 已知长方体ABCD-A1B1C1D1中，AB=1，BC=，AA1=，则直线C1D与直线BD1夹角的余弦值为 .‎ 二、 解答题：共70分.解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ 17. ‎（本小题满分12分）‎ 已知等差数列{an}的前n项和为Sn，且a3=-1，S7=7.‎ （1） 求数列{an}的通项公式an以及前n项和Sn；‎ （2） 若bn=（-1）n·an，求数列{bn}的前n项和Tn.‎ 18. 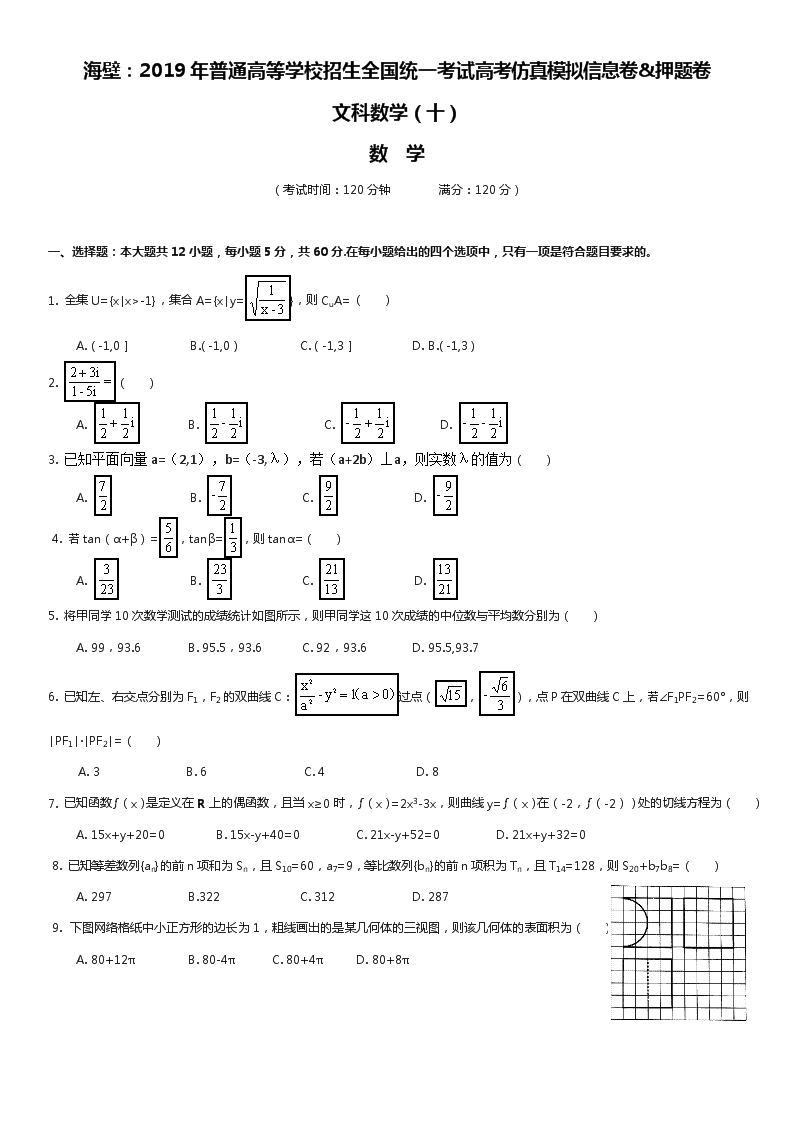‎（本小题满分12分）‎ 已知四棱锥S－ABCD中，AD⊥BD，∠CDB=∠CBD，E，F分别是SB，AB的中点。‎ （1） 若∠SDB=∠SBD，求证：SC⊥BD；‎ （2） 求证：平面CEF//平面SAD。‎ 13. 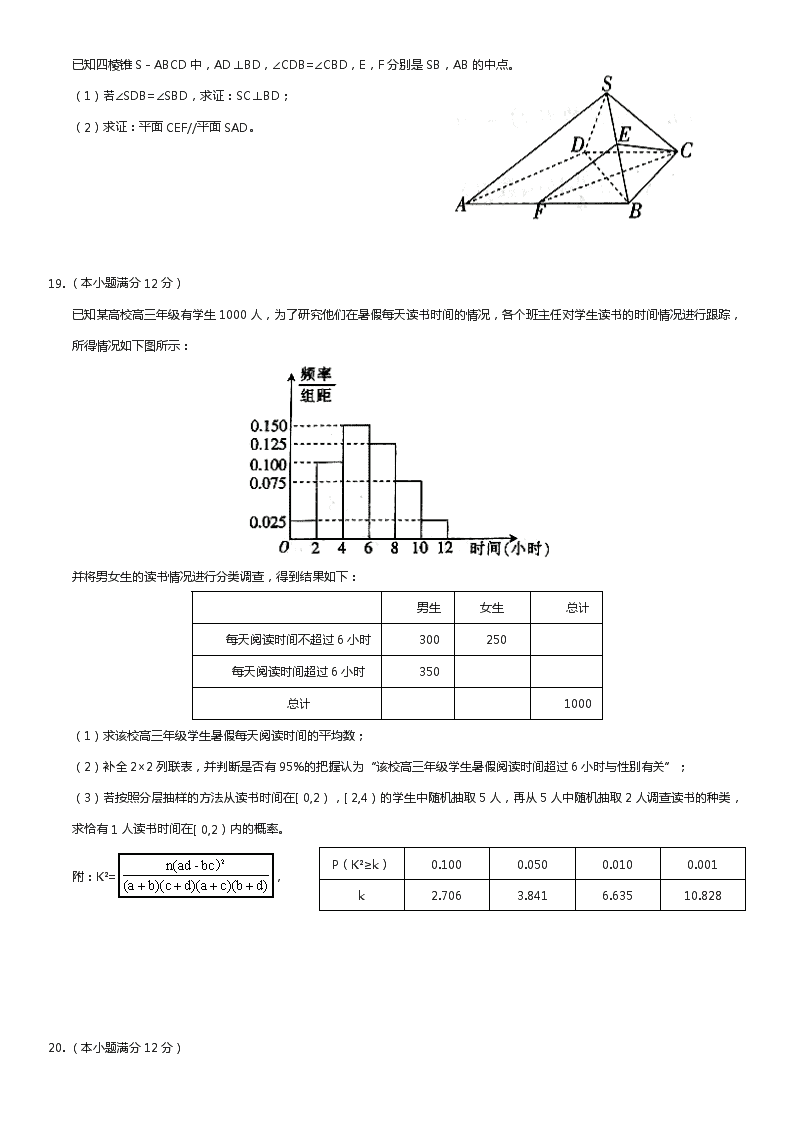‎（本小题满分12分）‎ ‎ 已知某高校高三年级有学生1000人，为了研究他们在暑假每天读书时间的情况，各个班主任对学生读书的时间情况进行跟踪，所得情况如下图所示：‎ ‎ 并将男女生的读书情况进行分类调查，得到结果如下：‎ 男生 女生 总计 每天阅读时间不超过6小时 ‎300‎ ‎250‎ 每天阅读时间超过6小时 ‎350‎ 总计 ‎1000‎ （1） 求该校高三年级学生暑假每天阅读时间的平均数；‎ （2） 补全2×2列联表，并判断是否有95%的把握认为“该校高三年级学生暑假阅读时间超过6小时与性别有关”；‎ （3） 若按照分层抽样的方法从读书时间在[ 0,2），[ 2,4）的学生中随机抽取5人，再从5人中随机抽取2人调查读书的种类，求恰有1人读书时间在[ 0,2）内的概率。‎ P（K²≥k）‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ 附：K²=，‎ 14. ‎（本小题满分12分）‎ 已知抛物线C：x²=2y，直线l：16x-8y+9=0，点A在抛物线C上运动但不在直线l上。‎ （1） 判断直线l′：x+y+2=0与抛物线C的位置关系，并说明理由；‎ （2） 若AB⊥x轴，且直线AB与直线l交于点P，AQ⊥l，垂足为Q，E（，），探究：是否为定值；若是，请求 出该定值，若不是，请说明理由。‎ 13. ‎（本小题满分12分）‎ 已知函数ƒ（x）=2（x-1）ex+ax2.‎ （1） 若a=e，求函数ƒ（x）的极值；‎ （2） 若函数ƒ（x）有2个零点，求实数a的取值范围。‎ ‎（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ 14. ‎（本小题满分10分）【选修4-4：坐标系与参数方程】‎ 已知极坐标系中，点M（，），曲线C的极坐标方程为ρ²cos²θ+3ρ²sin²θ-12=0，点N在曲线C上运动，以极点为 坐标原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程为（t为参数）。‎ （1） 求直线l的极坐标方程与曲线C的参数方程；‎ （2） 求线段MN的中点P到直线l的距离的最大值。‎ 13. ‎（本小题满分10分）【选修4-5：不等式选讲】‎ 已知函数ƒ（x）=∣x-1∣-∣2x-3∣.‎ （1） 求不等式ƒ（x）>-2的解集；‎ （2） 若x∈R，使得ƒ（x）≤m-成立，求实数m的取值范围。‎