高考文科数学湖南卷 11页

2008 年普通高等学校招生全国统一考试（湖南卷） 数 学（文史类） 一、选择题：本大题共 8 小题，每小题 5 分，共 40 分。在每小题给出的四个选项中， 只有一项是符合题目要求的。 1． 的值为 A． B． C． D． 2．抛物线 的焦点坐标是 A．（2，0） B．（- 2，0） C．（4，0） D．（- 4，0） 3．设 是等差数列 的前 n 项和，已知 ， ，则 等于 A．13 B．35 C．49 D． 63 4．如图 1， D，E，F 分别是 ABC 的边 AB，BC，CA 的中点，则 A． B． C． D． 5．某地政府召集 5 家企业的负责人开会，其中甲企业有 2 人到会，其余 4 家企业各有 1 人 到会，会上有 3 人发言，则这 3 人来自 3 家不同企业的可能情况的种数为 A．14 B．16 C．20 D．48 6．平面六面体 中，既与 共面也与 共面的棱的条数为 A．3 B．4 C．5 D．6 7．若函数 的导函数在区间 上是增函数，则函数 在区间 上的 图象可能是 A ． B． C． D． 2log 2 2− 2 1 2 − 1 2 2 8y x= − nS { }na 2 3a = 6 11a = 7S ∆ 0AD BE CF+ + =    0BD CF DF− + =    0AD CE CF+ − =    0BD BE FC− − =    1 1 1 1ABCD A B C D− AB 1CC ( )y f x= [ , ]a b ( )y f x= [ , ]a b y ababa o xo x y ba o x y o x y b 8．设函数 在 内有定义，对于给定的正数 K，定义函数 取函数 。当 = 时，函数 的单调递增区间为 A ． B． C ． D ． 二、填空题：本大题共 7 小题，每小题 5 分，共 35 分.把答案填在答题卡中对应题号后的 横线上。 9 ．某班共 30 人，其中 15 人喜爱篮球运动，10 人喜爱乒乓球运动，8 人对这两项 运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为 . 10．若 ，则 的最小值为 . 11．在 的展开式中， 的系数为 6 (用数字作答). 12． 一个总体分为 A，B 两层，用分层抽样方法从总体中抽取一个容量为 10 的样本。 已知 B 层中每个个体被抽到的概率都为 ，则总体中的个体数为 . 13．过双曲线 C： 的一个焦点作圆 的两条切线， 切点分别为 A，B，若 （O 是坐标原点），则双曲线线 C 的离心率为 . 14．在锐角 中， 则 的值等 于 ， 的取值范围为 . 15．如图 2，两块斜边长相等的直角三角板拼在一起， 若 ，则 ， . 三、解答题：本大题共 6 小题，共 75 分.解答应写出文字说明、证明过程或演算步骤. 16．（每小题满分 12 分） 已知向量 （Ⅰ）若 ，求 的值； （Ⅱ）若 求 的值。 ( )y f x= ( , )−∞ +∞ ( ), ( ) ,( ) , ( ) .K f x f x Kf x K f x K ≤=  > ( ) 2 xf x −= K 1 2 ( )Kf x ( ,0)−∞ (0, )+∞ ( , 1)−∞ − (1, )+∞ 0x > 2x x + 4(1 )x+ x 1 12 2 2 2 2 1x y a b − = ( 0, 0)a b> > 2 2 2x y a+ = 120AOB∠ =  ABC∆ 1, 2 ,BC B A= = cos AC A AC AD xAB yAC= +   x = y = (sin ,cos 2sin ), (1,2).a bθ θ θ= − =  / /a b  tanθ | | | |,0 ,a b θ π= < <  θ 17．（本小题满分 12 分） 为拉动经济增长，某市决定新建一批重点工程，分别为基础设施工程、民生工程和产业 建设工程三类，这三类工程所含项目的个数分别占总数的 、 、 .现有 3 名工人独 立地从中任选一个项目参与建设.求： （I）他们选择的项目所属类别互不相同的概率； （II）至少有 1 人选择的项目属于民生工程的概率. 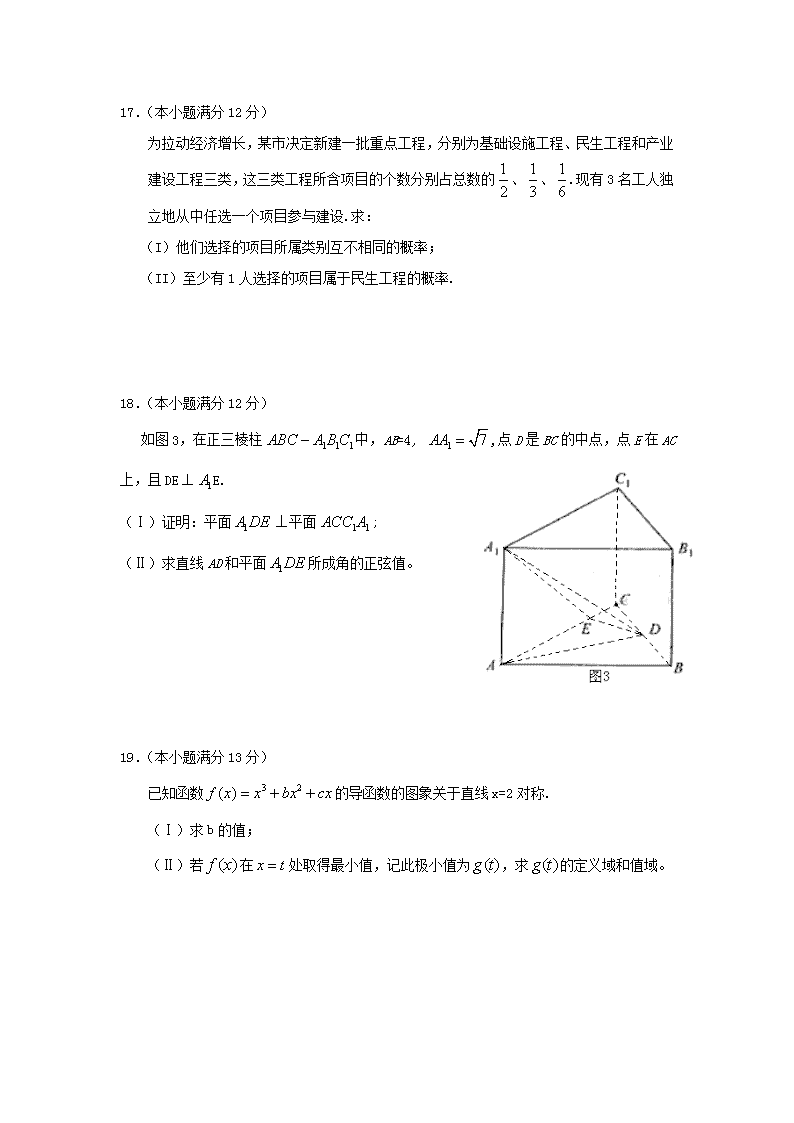18．（本小题满分 12 分） 如图 3，在正三棱柱 中，AB=4, ,点 D 是 BC 的中点，点 E 在 AC 上，且 DE E. （Ⅰ）证明：平面 平面 ; （Ⅱ）求直线 AD 和平面 所成角的正弦值。 19．（本小题满分 13 分） 已知函数 的导函数的图象关于直线 x=2 对称. （Ⅰ）求 b 的值； （Ⅱ）若 在 处取得最小值，记此极小值为 ，求 的定义域和值域。 1 2 1 3 1 6 1 1 1ABC A B C− 1 7AA = ⊥ 1A 1A DE ⊥ 1 1ACC A 1A DE 3 2( )f x x bx cx= + + ( )f x x t= ( )g t ( )g t 20．（本小题满分 13 分） 已知椭圆 C 的中心在原点，焦点在 轴上，以两个焦点和短轴的两个端点 为顶点的四边形是一个面积为 8 的正方形（记为 Q）. （Ⅰ）求椭圆 C 的方程; （Ⅱ）设点 P 是椭圆 C 的左准线与 轴的交点，过点 P 的直线 与椭圆 C 相交于 M,N 两 点，当线段 MN 的中点落在正方形 Q 内（包括边界）时，求直线 的斜率的取值范围。 21．（本小题满分 13 分） 对于数列 ,若存在常数 M＞0,对任意的 ，恒有 , 则称数列 为 数列. （Ⅰ）首项为 1，公比为 的等比数列是否为 B-数列？请说明理由; （Ⅱ）设 是数列 的前 n 项和.给出下列两组判断： A 组：①数列 是 B-数列, ②数列 不是 B-数列; B 组：③数列 是 B-数列, ④数列 不是 B-数列. 请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题. 判断所给命题的真假，并证明你的结论； (Ⅲ)若数列 是 B-数列，证明：数列 也是 B-数列。 x x l l { }nu *n N∈ 1 1 2 1n n n nu u u u u u M+ −− + − + + − ≤ { }nu B − 1 2 − nS { }nx { }nx { }nx { }nS { }nS { }na 2{ }na C 1D 1 B 1A 1 D C BA 参考答案及解析 一、选择题：本大题共 8 小题，每小题 5 分，共 40 分。 1．解:由 ,易知 D 正确. 2．解:由 ,易知焦点坐标是 ，故选 B. 3．解: 故选 C. 或由 , 所以 故选 C. 4．解: 得 ，故选 A. 或 . 5．解:由间接法得 ，故选 B. 6．解:如图，用列举法知合要求的棱为： 、 、 、 、 ，故选 C. 7．解: 因为函数 的导函数 在区间 上是增函数，即在区间 上 各点处的斜率 是递增的，由图易知选 A. 注意 C 中 为常数噢. 8．解: 函数 ，作图易知 ， 故在 上是单调递增的，选 C. 二、填空题：本大题共 7 小题，每小题 5 分，共 35 分.把答案填在答题卡中对应题号后的 横线上。 9 ．解: 设所求人数为 ，则只喜爱乒乓球运动的人数为 ， 故 . 注：最好作出韦恩图！ 10．解: ，当且仅当 时取等号. 11．解: ，故 得 的系数为 1 2 2 2 2 1 1log 2 log 2 log 22 2 = = = 2 8y x= − ( ,0) ( 2,0)2 p− = − 1 7 2 6 7 7( ) 7( ) 7(3 11) 49.2 2 2 a a a aS + + += = = = 2 1 1 6 1 3 1 5 11 2 a a d a a a d d = + = = ⇒ = + = = 7 1 6 2 13.a = + × = 1 7 7 7( ) 7(1 13) 49.2 2 a aS + += = = , ,AD DB AD BE DB BE DE FC= ∴ + = + = =         0AD BE CF+ + =    0AD BE CF AD DF CF AF CF+ + = + + = + =         3 2 1 6 2 4 20 4 16C C C− ⋅ = − = BC CD 1 1C D 1BB 1AA ( )y f x= ( )y f x′= [ , ]a b [ , ]a b k y k′ = 1( ) 2 ( )2 x xf x −= = 1( ) 2f x K≤ = ⇒ ( , 1] [1, )x∈ −∞ − +∞ ( , 1)−∞ − x 10 (15 ) 5x x− − = − 15 5 30 8 12x x+ − = − ⇒ = 0x > 2 2 2x x ⇒ + ≥ 2 2x xx = ⇒ = 2 1 4 4( ) ( ) r r r r rT C x C x+⇒ = = 2r = x 2 4 6.C = 12． 解: 设总体中的个体数为 ，则 13．解: , 14．解: 设 由正弦定理得 由锐角 得 ， 又 ，故 ， 15．解:作 ,设 ， , 由 解得 故 三、解答题：本大题共 6 小题，共 75 分.解答应写出文字说明、证明过程或演算步骤. 16．（每小题满分 12 分） 解：（Ⅰ） 因为 ，所以 于是 ，故 （Ⅱ）由 知， 所以 从而 ，即 ， 于是 .又由 知， ， 所以 ，或 . 因此 ，或 17．（本小题满分 12 分） 解: 记第 名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件 i=1，2，3.由题意知 相互独立， 相互独立， x 10 1 120.12 xx = ⇒ = 120 60 30 2AOB AOF AFO c a∠ = ⇒ ∠ = ⇒ ∠ = ⇒ =   2.ce a ∴ = = , 2 .A Bθ θ∠ = ⇒ = , 1 2.sin 2 sin 2cos cos AC BC AC AC θ θ θ θ= ∴ = ⇒ = ABC∆ 0 2 90 0 45θ θ< < ⇒ < <    0 180 3 90 30 60θ θ< − < ⇒ < <     2 330 45 cos2 2 θ θ< < ⇒ < <  2cos ( 2, 3).AC θ∴ = ∈ DF AB⊥ 1 2AB AC BC DE= = ⇒ = = 60DEB∠ =  6 ,2BD∴ = 45DBF∠ =  6 2 3 ,2 2 2DF BF= = × = 31 ,2x = + 3 .2y = / /a b  2sin cos 2sin ,θ θ θ= − 4sin cosθ θ= 1tan .4 θ = | | | |a b=  2 2sin (cos 2sin ) 5,θ θ θ+ − = 21 2sin 2 4sin 5.θ θ− + = 2sin 2 2(1 cos2 ) 4θ θ− + − = sin 2 cos2 1θ θ+ = − 2sin(2 )4 2 πθ + = − 0 θ π< < 924 4 4 π π πθ< + < 52 4 4 π πθ + = 72 4 4 π πθ + = 2 πθ = 3 .4 πθ = i , , ,i i iA B C 1 2 3, ,A A A 1 2 3, ,B B B 1 2 3, ,C C C 相互独立， （i，j，k=1，2，3，且 i，j，k 互不相同）相互独立， 且 （Ⅰ）他们选择的项目所属类别互不相同的概率 P= （Ⅱ）至少有 1 人选择的项目属于民生工程的概率 P= 18．（本小题满分 12 分） 解 : （ Ⅰ ） 如 图 所 示 ， 由 正 三 棱 柱 的性质知 平面 . 又 DE 平面 ABC，所以 DE .而 DE E， , 所以 DE⊥平面 .又 DE 平面 ， 故平面 ⊥平面 . （Ⅱ）解法 1: 过点 A 作 AF 垂直 于点 , 连接 DF.由（Ⅰ）知，平面 ⊥平面 ， 所以 AF 平面 ,故 是直线 AD 和 平面 所成的角。 因为 DE ， 所以 DE AC.而 ABC 是边长为 4 的正三角形， 于是 AD= ，AE=4-CE=4- =3. 又因为 ，所以 E= = 4, , . , ,i j kA B C 1 1 1( ) , ( ) , ( ) .2 3 6i i iP A P B P C= = = 1 2 33! ( )P A B C 1 2 36 ( ) ( ) ( )P A P B P C= 1 1 1 16 .2 3 6 6 = × × × = 1 2 31 ( )P B B B− 1 2 31 ( ) ( ) ( )P B P B P B= − 31 191 (1 ) .3 27 = − − = 1 1 1ABC A B C− 1AA ⊥ ABC ⊂ 1AA⊥ ⊥ 1A 1 1 1AA A E A= 1 1ACC A ⊂ 1A DE 1A DE 1 1ACC A 1A E F 1A DE 1 1ACC A ⊥ 1A DE ADF∠ 1A DE ⊥ 1 1ACC A ⊥ ∆ 2 3 1 2 CD 1 7AA = 1A 2 2 1 1A E AA AE= + 2 2( 7) 3= + 1 1 3 7 4 AE AAAF A E ⋅= = 21sin 8 AFADF AD ∠ = = 即直线 AD 和平面 所成角的正弦值为 . 解法 2 : 如图所示，设 O 是 AC 的中点，以 O 为原点建立空间直角坐标系， 则相关各点的坐标分别是 A(2,0,0,), (2,0, ), D(-1, ,0), E(-1,0,0). 易知 =（-3， ，- ）， =（0，- ，0）， =（-3， ，0）. 设 是平面 的一个法向量，则 解得 . 故可取 .于是 = . 由此即知，直线 AD 和平面 所成角的正弦值为 . 19．（本小题满分 13 分） 解: （Ⅰ） .因为函数 的图象关于直线 x=2 对称， 所以 ，于是 （ Ⅱ ） 由 （ Ⅰ ） 知 ， ， . （ⅰ）当 c 12 时， ，此时 无极值。 （ii）当 c<12 时， 有两个互异实根 , .不妨设 ＜ ，则 ＜2＜ . 当 x＜ 时， ， 在区间 内为增函数； 当 ＜x＜ 时， ， 在区间 内为减函数; 1A DE 21 8 1A 7 3 1A D 3 7 DE 3 AD 3 ( , , )n x y z= 1A DE 1 3 0, 3 3 7 0. n DE y n A D x y z  ⋅ = − = ⋅ = − + − =     7 , 03x z y= − = ( 7,0, 3)n = − cos , n ADn AD n AD ⋅= ⋅      3 7 21 84 2 3 − = − × 1A DE 21 8 2( ) 3 2f x x bx c′ = + + ( )f x′ 2 26 b− = 6.b = − 3 2( ) 6f x x x cx= − + 2 2( ) 3 12 3( 2) 12f x x x c x c′ = − + = − + − ≥ ( ) 0f x′ ≥ ( )f x ( ) 0f x′ = 1x 2x 1x 2x 1x 2x 1x ( ) 0f x′ > ( )f x 1( , )x−∞ 1x 2x ( ) 0f x′ < ( )f x 1 2( , )x x 当 时， ， 在区间 内为增函数. 所以 在 处取极大值，在 处取极小值. 因此，当且仅当 时，函数 在 处存在唯一极小值，所以 . 于是 的定义域为 .由 得 . 于是 . 当 时， 所以函数 在区间 内是减函数，故 的值域为 20．（本小题满分 13 分） 解: （Ⅰ）依题意，设椭圆 C 的方程为 焦距为 ， 由题设条件知， 所以 故椭圆 C 的方程为 . （Ⅱ）椭圆 C 的左准线方程为 所以点 P 的坐标 ， 显然直线 的斜率 存在，所以直线 的方程为 。 如图，设点 M，N 的坐标分别为 线段 MN 的中点为 G ， 由 得 . ……① 2x x> ( ) 0f x′ > ( )f x 2( , )x +∞ ( )f x 1x x= 2x x= 12c < ( )f x 2x x= 2 2t x= > ( )g t (2, )+∞ 2( ) 3 12 0f t t t c′ = − + = 23 12c t t= − + 3 2 3 2( ) ( ) 6 2 6 , (2, )g t f t t t ct t t t= = − + = − + ∈ +∞ 2t > 2( ) 6 12 6 (2 ) 0,g t t t t t′ = − + = − < ( )g t (2, )+∞ ( )g t ( ,8).−∞ 2 2 2 2 1( 0),x y a ba b + = > > 2c 2 8, ,a b c= = 2 21 4.2b a= = 2 2 18 4 x y+ = 4,x = − ( 4,0)− l k l ( 4)y k x= + 1 1 2 2( , ),( , ),x y x y 0 0( , )x y 2 2 ( 4), 18 4 y k x x y = + + = 2 2 2 2(1 2 ) 16 32 8 0k x k x k+ + + − = 由 解得 . ……② 因为 是方程①的两根，所以 ，于是 = ， . 因为 ，所以点 G 不可能在 轴的右边， 又直线 , 方程分别为 所以点 在正方形 内（包括边界）的充要条件为 即 亦即 解得 ，此时②也成立. 故直线 斜率的取值范围是 21．（本小题满分 13 分） 解: （Ⅰ）设满足题设的等比数列为 ,则 .于是 = = 所以首项为 1，公比为 的等比数列是 B-数列 . （Ⅱ）命题 1：若数列 是 B-数列，则数列 是 B-数列.此命题为假命题. 事实上设 =1， ，易知数列 是 B-数列，但 =n， 2 2 2 2(16 ) 4(1 2 )(32 8) 0k k k∆ = − + − > 2 2 2 2k− < < 1 2,x x 2 1 2 2 16 1 2 kx x k + = − + 1 2 0 2 x xx += 2 2 8 1 2 k k − + 0 0 2 4( 4) 1 2 ky k x k = + = + 2 0 2 8 01 2 kx k = − ≤+ y 1 2F B 1 1F B 2, 2,y x y x= + = − − G Q 0 0 0 0 2, 2. y x y x ≤ +  ≥ − 2 2 2 2 2 2 4 8 2,1 2 1 2 4 8 2,1 2 1 2 k k k k k k k k  ≤ − + + +  ≥ − + + 2 2 2 2 1 0, 2 2 1 0. k k k k  + − ≤ − − ≤ 3 1 3 1 2 2k − −− ≤ ≤ l 3 1 3 1[ , ].2 2 − −− { }na 11( )2 n na −= − 1 2 2 1 1 1 3 1( ) ( ) ( ) , 2.2 2 2 2 n n n n na a n− − − −− = − − − = × ≥ 1 1 2 1| | | | | |n n n na a a a a a+ −− + − + + − 2 n3 1 1 112 2 2 2  × + + + +   - 1（ ） （ ） n13 1 3.2  × − <  （ ） 1 2 − { }nx { }nS nx *n N∈ { }nx nS . 由 n 的任意性知，数列 不是 B-数列。 命题 2：若数列 是 B-数列，则数列 不是 B-数列。此命题为真命题。 事实上，因为数列 是 B-数列，所以存在正数 M，对任意的 ，有 , 即 .于是 , 所以数列 是 B-数列。 （注：按题中要求组成其它命题解答时，仿上述解法） (Ⅲ)若数列 是 B-数列，则存在正数 M，对任意的 有 . 因为 . 记 ，则有 . 因此 . 故数列 是 B-数列. 1 1 2 1| | | | | |n n n nS S S S S S n+ −− + − + + − = { }nS { }nS { }nx { }nS *n N∈ 1 1 2 1| | | | | |n n n nS S S S S S M+ −− + − + + − ≤ 1 2| | | | | |n nx x x M+ + + + ≤ 1 1 2 1n n n nx x x x x x+ −− + − + + − 1 1 2 1 12 2 2 2n n nx x x x x M x+ −≤ + + + + + ≤ + { }nx { }na ,n N •∈ 1 1 2 1n n n na a a a a a M+ −− + − + + − ≤ 1 1 2 2 1 1n n n n na a a a a a a a− − −= − + + + + − + 1 1 2 2 1 1 1n n n na a a a a a a M a− − −≤ − + − + + − + ≤ + 1K M a= + 2 2 1 1 1( )( )n n n n n na a a a a a+ + +− = + − 1 1 1( ) 2n n n n n na a a a K a a+ + +≤ + − ≤ − 2 2 2 2 2 2 1 1 2 1... 2n n n na a a a a a KM+ −− + − + + − ≤ { }2 na