高考试题福建卷数学试题理 4页

‎2004年高考试题福建卷数学试题（理工类）‎ 数学试题（理工农医类）‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项最符合题目要求的.‎ ‎（1）复数的值是 ‎（A） （B） （C） （D）‎ ‎（2）等于 ‎（A）2 （B） （C）4 （D）‎ ‎（3）命题p：若a、b∈R，则|a|+|b|>1是|a+b|>1的充分不必要条件.‎ ‎ 命题q：函数的定义域是.则 ‎（A）“p或q”为假 （B）“p且q”为真 （C）p真q假 （D）p假p真 ‎（4）已知F1、F2是椭圆的两个焦点，过F1且与椭圆长轴垂直的直线交椭圆于A、B两点，△ABF2是正三角形，则这个椭圆的离心率是 ‎（A） （B） （C） （D）‎ ‎（5）已知m、n是不重合的直线，、是不重合的平面，有下列命题：‎ 若则；‎ 若则；‎ 若则且；‎ 若则.‎ 其中真命题的个数是 ‎（A）0 　（B）1 　　 （C）2 　　　 （D）3‎ ‎（6） 某校高二年级共有六个班级，现从外地转入4名学生，要安排到该年级的两个班级且每班安排2名，则不同的安排方案种数为 ‎（A） （B） （C） （D）‎ ‎（7）已知函数的函数是，则的图象是 ‎1‎ ‎1‎ O y x ‎（A）‎ ‎1‎ ‎1‎ O y x ‎（C）‎ ‎1‎ ‎1‎ O y x ‎（B）‎ y ‎1‎ ‎1‎ O x ‎（D）‎ ‎（8）已知a、b是非零向量且满足，则a与b的夹角是 ‎（A） （B） （C） （D）‎ ‎（9）若展开式的第3项为288，则的值是 ‎（A）2 （B）1 （C） （D）‎ O C B A ‎（10）如图，A、B、C是表面积为48π的球面上三点，AB=2，BC=4，∠ABC=60°，O为球心，则直线OA与截面ABC所成的角是 ‎（A） （B） ‎ ‎（C） （D）‎ ‎（11）定义在R上的函数满足，当时，，则 ‎（A） （B）‎ ‎（C） （D）‎ P A C M Q B 北 东 ‎（12）如图，B地在A地的正东方向４km处，C地在B地的北偏东30°方向2km处，河流的沿岸PQ（曲线）上任意一点到A的距离比到B的距离远2km.现要在曲线PQ上选一处M建一座码头，向B、C两地转运货物.经测算，从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km，那么修建这两条公路的总费用最低是 ‎（A）万元 ‎ ‎（B）万元 ‎ ‎（C）万元 ‎ ‎（D）万元 第Ⅱ卷 二、填空题：本大题共4个小题，每小题4分，共16分.把答案填在题中横线上.‎ ‎（13）直线被曲线所截得的弦长等于 .‎ ‎（14）设函数在处连续，则实数的值为 .‎ ‎（15）某射手射击1次，击中目标的概率是0.9.他连续射击4次，且各次射击是否击中目标相互之间没有影响.有下列结论：‎ 他第3次击中目标的概率是0.9；‎ 他恰好击中目标3次的概率是0.93×0.1；‎ 他至少击中目标1次的概率是1-0.14.‎ 其中正确结论的序号是 （写出所有正确结论的序号）.‎ ‎（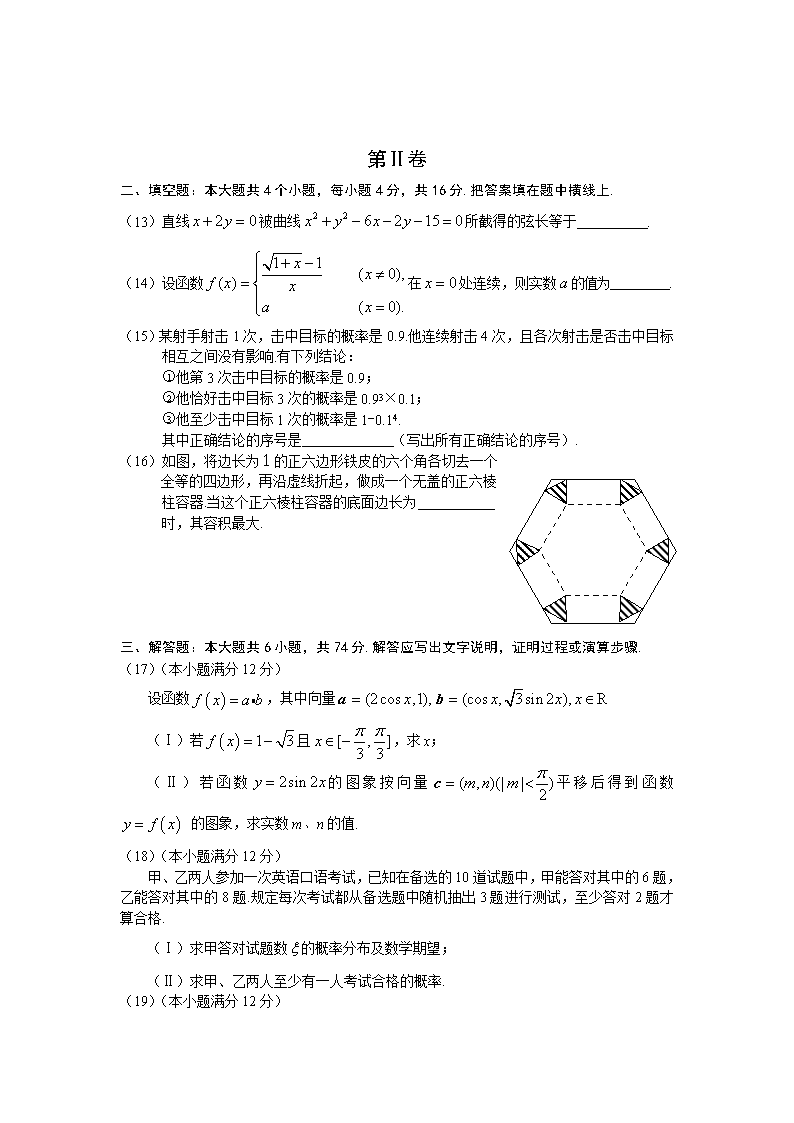16）如图，将边长为１的正六边形铁皮的六个角各切去一个 全等的四边形，再沿虚线折起，做成一个无盖的正六棱 柱容器.当这个正六棱柱容器的底面边长为 ‎ 时，其容积最大.‎ 三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.‎ ‎（17）（本小题满分12分）‎ 设函数，其中向量 ‎（Ⅰ）若且，求x；‎ ‎（Ⅱ）若函数的图象按向量平移后得到函数 的图象，求实数m、n的值.‎ ‎（18）（本小题满分12分）‎ 甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格.‎ ‎（Ⅰ）求甲答对试题数的概率分布及数学期望；‎ ‎（Ⅱ）求甲、乙两人至少有一人考试合格的概率.‎ ‎（19）（本小题满分12分）‎ 在三棱锥中，是边长为4的正三角形，平面，、分别为、的中点.‎ B C A S M N ‎（Ⅰ）证明；‎ ‎（Ⅱ）求二面角的大小；‎ ‎（Ⅲ）求点B到平面CMN的距离.‎ ‎（20）（本小题满分12分）‎ 某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降.若不进行改造，预测从今年起每年比上一年纯利润减少20万元.今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润为万元（n为正整数）.‎ ‎（Ⅰ）设从今年起的前n年，若该企业不进行技术改造的累计纯利润为An万元，进行技术改造后的累计纯利润为Bn万元（须扣除技术改造资金），求An、Bn的表达式；‎ ‎（Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？‎ ‎（21）（本小题满分12分）‎ 已知在区间上是增函数.‎ ‎（Ⅰ）求实数a的值所组成的集合A；‎ ‎（Ⅱ）设关于x的方程的两根为、.试问：是否存在实数m，使得不等式对任意及恒成立？若存在，求出m的取值范围；若不存在，请说明理由.‎ ‎（22）（本小题满分14分）‎ x y T P M O Q l 如图，P是抛物线C：上一点，直线l过 点P且与抛物线C交于另一点Q.‎ ‎（Ⅰ）若直线l与过点P的切线垂直，求线段PQ 中点M的轨迹方程；‎ ‎（Ⅱ）若直线l不过原点且与x轴交于点S，与y 轴交于点T，试求的取值范围.‎