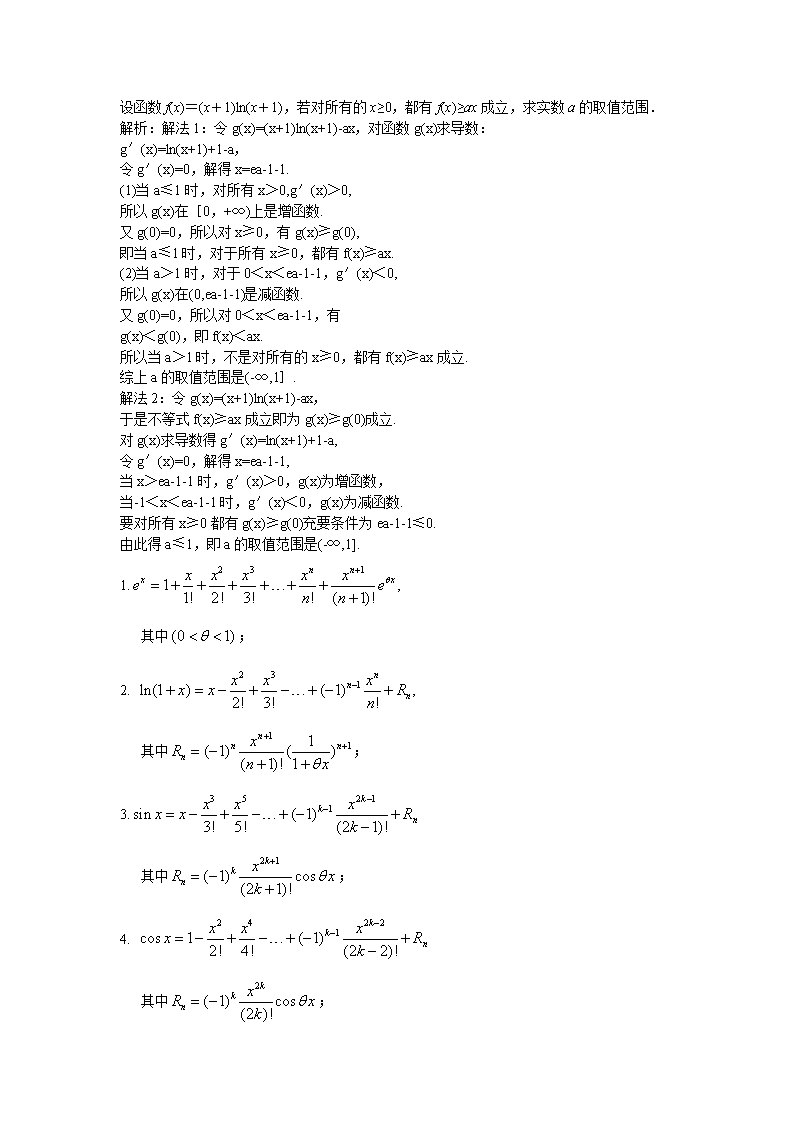导数结合洛必达法则巧解高考压轴题 7页

设函数f(x)＝(x＋1)ln(x＋1)，若对所有的x≥0，都有f(x)≥ax成立，求实数a的取值范围．‎ 解析：解法1：令g(x)=(x+1)ln(x+1)-ax，对函数g(x)求导数：‎ g′(x)=ln(x+1)+1-a，‎ 令g′(x)=0，解得x=ea-1-1.‎ ‎(1)当a≤1时，对所有x＞0,g′(x)＞0,‎ 所以g(x)在［0，+∞)上是增函数.‎ 又g(0)=0，所以对x≥0，有g(x)≥g(0),‎ 即当a≤1时，对于所有x≥0，都有f(x)≥ax.‎ ‎(2)当a＞1时，对于0＜x＜ea-1-1，g′(x)＜0,‎ 所以g(x)在(0,ea-1-1)是减函数.‎ 又g(0)=0，所以对0＜x＜ea-1-1，有 g(x)＜g(0)，即f(x)＜ax.‎ 所以当a＞1时，不是对所有的x≥0，都有f(x)≥ax成立.‎ 综上a的取值范围是(-∞,1］.‎ 解法2：令g(x)=(x+1)ln(x+1)-ax，‎ 于是不等式f(x)≥ax成立即为g(x)≥g(0)成立.‎ 对g(x)求导数得g′(x)=ln(x+1)+1-a,‎ 令g′(x)=0，解得x=ea-1-1,‎ 当x＞ea-1-1时，g′(x)＞0，g(x)为增函数，‎ 当-1＜x＜ea-1-1时，g′(x)＜0，g(x)为减函数.‎ 要对所有x≥0都有g(x)≥g(0)充要条件为ea-1-1≤0.‎ 由此得a≤1，即a的取值范围是(-∞,1].‎ ‎1.‎ 其中；‎ ‎2. ‎ 其中；‎ ‎3.‎ 其中；‎ ‎4. ‎ 其中；‎ 已知函数，曲线在点处的切线方程为.‎ ‎（Ⅰ）求、的值；‎ ‎（Ⅱ）如果当，且时，，求的取值范围.‎ ‎（Ⅰ）略解得，.‎ ‎（Ⅱ）方法一：分类讨论、假设反证法 由（Ⅰ）知，所以.‎ 考虑函数，则.‎ ‎(i)当时，由知，当时，.因为，‎ 所以当时，，可得；当时，，可得 ‎，从而当且时，，即；‎ ‎（ii）当时，由于当时，，故，而，故当时，，可得，与题设矛盾.‎ ‎（iii）当时， ，而，故当时，，可得，与题设矛盾.综上可得，的取值范围为.‎ 当，且时，，即，‎ 也即，记，，且 则，‎ 记，则，‎ 从而在上单调递增，且，因此当时，，当时，；当时，，当时，，所以在 上单调递减，在上单调递增.‎ 由洛必达法则有 ‎ ‎，‎ 即当时，，即当，且时，.‎ 因为恒成立，所以.综上所述，当，且时，成立，的取值范围为.‎ 设函数.‎ ‎（Ⅰ）若，求的单调区间；‎ ‎（Ⅱ）当时，，求的取值范围.‎ 应用洛必达法则和导数 ‎（Ⅱ）当时，，即.‎ ‎①当时，；②当时，等价于.‎ 记 ，则. ‎ 记 ，则，当时，，所以在上单调递增，且，所以在上单调递增，且，因此当时，，从而在上单调递增.‎ 由洛必达法则有，‎ 即当时，，所以当时，所以，因此.‎ 综上所述，当且时，成立.‎ 若不等式对于恒成立，求的取值范围.‎ 应用洛必达法则和导数 当时，原不等式等价于.‎ 记，则.‎ 记，则.‎ 因为，‎ ‎，所以在上单调递减，且，‎ 所以在上单调递减，且.因此在上单调递减，‎ 且，故，因此在上单调递减.‎ 由洛必达法则有 ‎，‎ 即当时，，即有.‎ 故时，不等式对于恒成立.‎ 通过以上例题的分析，我们不难发现应用洛必达法则解决的试题应满足：‎ ① 可以分离变量；‎ ‎②用导数可以确定分离变量后一端新函数的单调性；‎ ② 现“”型式子.‎ ‎2010海南宁夏文（21）‎ 已知函数.‎ ‎（Ⅰ）若在时有极值，求函数的解析式；‎ ‎（Ⅱ）当时，，求的取值范围.‎ 解：（Ⅰ）略 ‎（Ⅱ）应用洛必达法则和导数 当时，，即.‎ ‎①当时，；‎ ‎②当时，等价于，也即.‎ 记，，则.‎ 记，，则，因此在上单调递增，且，所以，从而在上单调递增.‎ 由洛必达法则有 ‎，‎ 即当时，‎ 所以，即有.‎ 综上所述，当，时，成立.‎ ‎2010全国大纲理（22）‎ 设函数.‎ ‎（Ⅰ）证明：当时，；‎ ‎（Ⅱ）设当时，，求的取值范围.‎ 解：（Ⅰ）略 ‎ ‎（Ⅱ）应用洛必达法则和导数 由题设，此时.‎ ‎①当时，若，则，不成立；‎ ‎②当时，当时，，即；‎ 若，则；‎ 若，则等价于，即.‎ 记，则.‎ 记，则，.‎ 因此，在上单调递增，且，所以，‎ 即在上单调递增，且，所以.‎ 因此，所以在上单调递增.‎ 由洛必达法则有 ‎，即当时，‎ ‎，即有，所以.综上所述，的取值范围是.‎ 设函数．‎ ‎（Ⅰ）求的单调区间；‎ ‎（Ⅱ）如果对任何，都有，求的取值范围．‎ 解：（Ⅰ）． ‎ 当（）时，，即；‎ 当（）时，，即．‎ 因此在每一个区间（）是增函数，‎ 在每一个区间（）是减函数． ‎ ‎（Ⅱ）应用洛必达法则和导数 若，则；‎ 若，则等价于，即 则.‎ 记，‎ 因此，当时，，在上单调递减，且，故，所以在上单调递减，‎ 而.‎ 另一方面，当时，，因此.‎