新教材高中物理第3章圆周运动知识网络建构与学科素养提升课件鲁科版必 15页

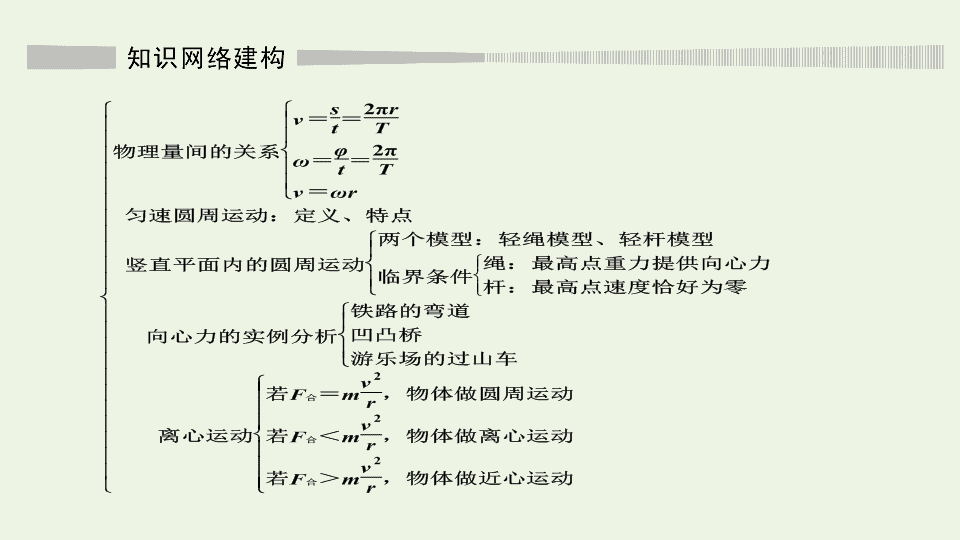
知识网络建构与学科素养提升 一、圆周运动中的多解问题 匀速圆周运动的多解问题常涉及两个物体的两种不同运动，其中一个做匀速圆周运动，另一个做其他形式的运动。因匀速圆周运动具有周期性，使得在一个周期中发生的事件在其他周期同样可能发生，这就要求我们在解决此类问题时，必须考虑多解的可能性，一般处理这类问题时，要把一个物体的运动时间 t ，与圆周运动的周期 T 建立起联系才会较快的解决问题。 [ 例 1] 如图所示，水平放置的圆筒绕其中心对称轴 OO ′ 匀速转动，筒壁上 P 处有一小圆孔，桶壁很薄，桶的半径 R ＝ 2 m ，圆孔正上方 h ＝ 3.2 m 处有一小球由静止开始下落，已知圆孔的半径略大于小球的半径。已知小球刚好能从孔中进入圆筒，并且与圆筒不发生碰撞离开圆筒。求： (1) 小球在圆筒中运动的时间？ (2) 圆筒转动的角速度是多大？ ( 空气阻力不计， g 取 10 m/s 2 ) 。 [ 针对训练 1] 如图所示是一种子弹测速器，甲、乙两圆盘均以角速度 ω 旋转，甲、乙两圆盘相距 d ，一个子弹 P 从甲盘某条半径 O 1 A 射入，从乙盘 O 2 B ′ 半径上射出，测得跟 O 1 A 平行的半径 O 2 B 与 O 2 B ′ 之间夹角为 θ ，子弹穿过盘时的阻力不计，求子弹的速度。 二、圆周运动中的临界问题 当物体从某种特性变化为另一种特性时，发生质的飞跃的转折状态，通常叫做临界状态。出现临界状态时，既可理解为 “ 恰好出现 ” ，也可理解为 “ 恰好不出现 ” 。 1. 水平面内的圆周运动的临界问题 在这类问题中，要特别注意分析物体做圆周运动的向心力来源，考虑达到临界条件时物体所处的状态，即临界速度、临界角速度，然后分析该状态下物体的受力特点，结合圆周运动知识，列方程求解。常见情况有以下两种： (1) 与绳的弹力有关的圆周运动临界问题。 (2) 因静摩擦力存在最值而产生的圆周运动临界问题。 2. 竖直面内的圆周运动的临界问题 (2) 用杆固定物体在竖直平面内做圆周运动。 此种情况下，由于物体所受的重力可以由杆给它的向上的支持力来平衡，所以在最高点时的速度可以为零。当物体在最高点的速度 v ≥ 0 时，物体就可以完成一个完整的圆周运动。 [ 例 2] 如图所示，水平转盘上放有一质量为 m 的物体 ( 可视为质点 ) ，连接物体和转轴的绳子长为 r ，物体与转盘间的最大静摩擦力是其压力的 μ 倍，转盘的角速度由零逐渐增大， g 为重力加速度。求： (1) 绳子对物体的拉力为零时的最大角速度。 [ 针对训练 2] 如图所示，轻杆长为 L ，一端固定在水平轴上的 O 点，另一端系一个小球 ( 可视为质点 ) 。小球以 O 为圆心在竖直平面内做圆周运动，且能通过最高点， g 为重力加速度。下列说法正确的是 ( 　　 ) 答案 　 A