浙江专版2021年高考物理一轮复习课时提升作业三十三动量动量守恒定律含解析 8页

- 1 - 动量　动量守恒定律 (建议用时 40 分钟) 1.(多选)如图所示,一个质量为 0.2 kg 的垒球,以 20 m/s 的水平速度飞向球棒,被球棒打击后 反向水平飞回,速度大小变为 40 m/s,设球棒与垒球的作用时间为 0.01 s。下列说法正确的是 (　　) A.球棒对垒球的平均作用力大小为 1 200 N B.球棒对垒球的平均作用力大小为 400 N C.球棒对垒球做的功为 120 J D.球棒对垒球做的功为 40 J 【解析】选 A、C。设球棒对垒球的平均作用力为 F,由动量定理得 ·t=m(vt-v0),取 vt=40 m/s,则 v0=-20 m/s,代入上式,得 =1 200 N,由动能定理得 W= m - m =120 J,选项 A、C 正确。 2.(2019·江苏高考)质量为 M 的小孩站在质量为 m 的滑板上,小孩和滑板均处于静止状态,忽 略滑板与地面间的摩擦。小孩沿水平方向跃离滑板,离开滑板时的速度大小为 v,此时滑板的速 度大小为 (　　) A. v　　B. v　　C. v　　D. v 【解析】选 B。设滑板的速度为 u,由小孩和滑板动量守恒得:0=mu-Mv,解得:u= v,故 B 正 确,A、C、D 错误。 3.我国在酒泉卫星发射中心用“长征四号”运载火箭成功发射硬 X 射线调制望远镜卫星“慧 眼”。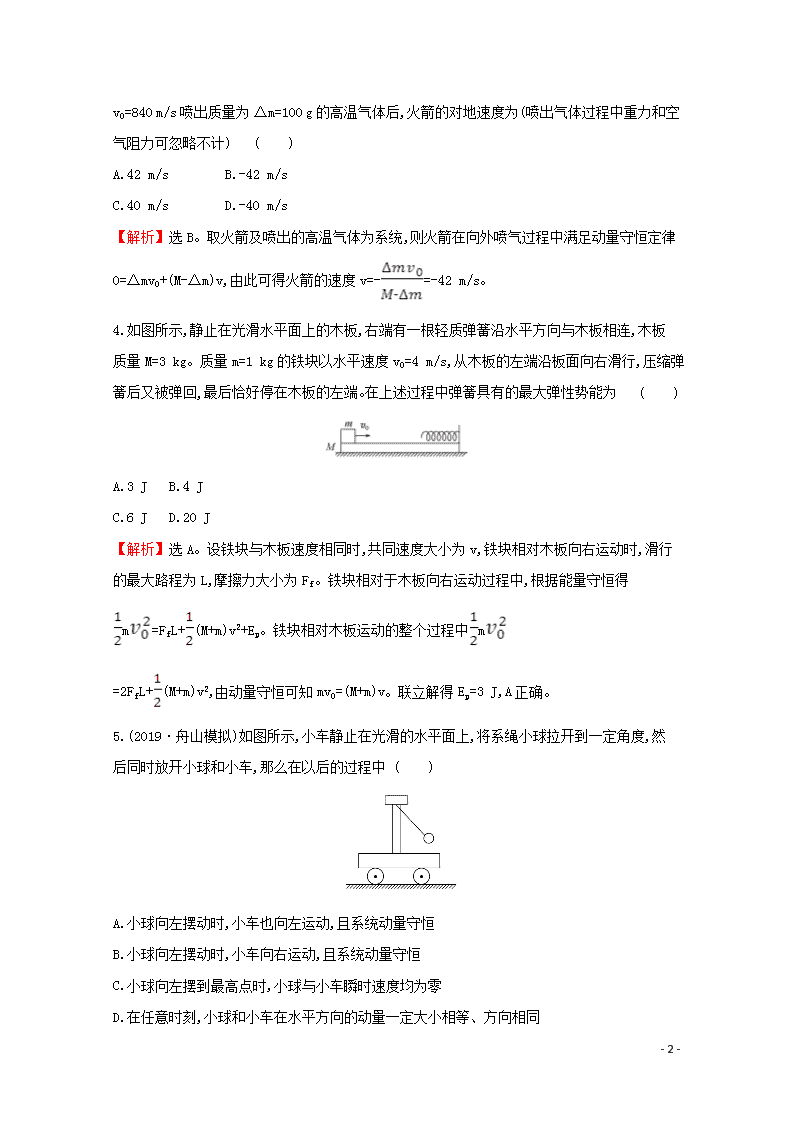假设将发射火箭看成如下模型:静止的实验火箭,总质量为 M=2100g,当它以对地速度为 - 2 - v0=840 m/s 喷出质量为 Δm=100 g 的高温气体后,火箭的对地速度为(喷出气体过程中重力和空 气阻力可忽略不计) (　　) A.42 m/s 　　 B.-42 m/s C.40 m/s D.-40 m/s 【解析】选 B。取火箭及喷出的高温气体为系统,则火箭在向外喷气过程中满足动量守恒定律 0=Δmv0+(M-Δm)v,由此可得火箭的速度 v=- =-42 m/s。 4.如图所示,静止在光滑水平面上的木板,右端有一根轻质弹簧沿水平方向与木板相连,木板 质量 M=3 kg。质量 m=1 kg 的铁块以水平速度 v0=4 m/s,从木板的左端沿板面向右滑行,压缩弹 簧后又被弹回,最后恰好停在木板的左端。在上述过程中弹簧具有的最大弹性势能为 (　　) A.3 J B.4 J C.6 J D.20 J 【解析】选 A。设铁块与木板速度相同时,共同速度大小为 v,铁块相对木板向右运动时,滑行 的最大路程为 L,摩擦力大小为 Ff。铁块相对于木板向右运动过程中,根据能量守恒得 m =FfL+ (M+m)v2+Ep。铁块相对木板运动的整个过程中 m =2FfL+ (M+m)v2,由动量守恒可知 mv0=(M+m)v。联立解得 Ep=3 J,A 正确。 5.(2019·舟山模拟)如图所示,小车静止在光滑的水平面上,将系绳小球拉开到一定角度,然 后同时放开小球和小车,那么在以后的过程中 (　　) A.小球向左摆动时,小车也向左运动,且系统动量守恒 B.小球向左摆动时,小车向右运动,且系统动量守恒 C.小球向左摆到最高点时,小球与小车瞬时速度均为零 - 3 - D.在任意时刻,小球和小车在水平方向的动量一定大小相等、方向相同 【解析】选 C。小球与小车组成的系统在水平方向不受外力,竖直方向所受外力不为零,故系统 只在水平方向动量守恒,系统在水平方向上总动量为零,小球与车在水平方向上的动量大小相 等、方向相反,小球向左摆动时,小车向右运动,故选项 A、B 错误;小球向左摆到最高点时,小 球的速度为零而小车的速度也为零,故选项 C 正确;系统只在水平方向动量守恒,在任意时刻, 小球和小车在水平方向的动量一定大小相等、方向相反,故选项 D 错误。 6.A、B 两球之间压缩一根轻弹簧,静置于光滑水平桌面上。已知 A、B 两球质量分别为 2m 和 m。当用板挡住 A 球而只释放 B 球时,B 球被弹出落于距桌边距离为 x 的水平地面上,如图所示。 当用同样的程度压缩弹簧,取走 A 左边的挡板,将 A、B 同时释放时,B 球的落地点距桌边距离为 (　　) A. 　　　B. x　　　C.x　　　D. x 【解析】选 D。当用板挡住小球 A 而只释放 B 球时,根据能量守恒:Ep= m ,根据平抛运动规 律有:x=v0t。当用同样的程度压缩弹簧,取走 A 左边的挡板,将 A、B 同时释放时,设 A、B 的速 度分别为 vA 和 vB,则根据动量守恒和能量守恒有:2mvA- mvB=0,Ep= ·2m + m ,解得 vB= v0,B 球的落地点距桌边距离为 x′=vBt= x,选项 D 正确。 7.(多选)A、B 两物体在一水平长直气垫导轨上相碰,碰撞前物体 A 做匀速直线运动,物体 B 静 止不动,频闪照相机每隔 0.1 s 闪光一次,连续拍照多次,拍得如图所示的照片,不计两物体的 大小及两物体碰撞过程所用的时间,则由此照片可判断 (　　) A.第四次拍照时物体 A 在 100 cm 处 B.第四次拍照时物体 A 在 80 cm 处 C.mA∶mB=3∶1 - 4 - D.mA∶mB=1∶3 【解析】选 A、D。碰撞前,物体 A 做匀速直线运动,可知物体 A 第三次在 90 cm 处,第四次在 100 cm 处,故 A 项正确,B 项错误;碰撞前,物体 A 的速度大小为 v0= = m/s=4 m/s,方向向右,碰撞后,物体 A 的速度大小为 vA= = m/s=2 m/s,方向向左, 物体 B 的速度大小为 vB= = m/s=2 m/s,方向向右,取向右为正方向,根据动量守恒定律得 mAv0=-mAvA+mBvB,代入数据得 mA×4=-mA×2+mB×2,解得 mA∶mB =1∶3,故 C 项错误,D 项正确。 8.(多选)(2019·杭州模拟)如图所示,三个完全相同且质量均为 m 的正方体叠放在水平面上; 锁定后正方体 2 的 4 个斜面均与水平方向成 45°角。若不计一切摩擦,解除锁定后,正方体 2 下落过程中未发生转动,下列说法正确的是 (　　) A.解除锁定前,正方体 2 对 1 的压力大小为 mg B.正方体 2 落地前的速度与正方体 1 的速度总是大小相等 C.正方体 2 落地前,1、2、3 构成的系统机械能不守恒 D.正方体 2 落地前,1、2、3 构成的系统动量守恒 【解析】选 A、B。解除锁定前,对正方体 2 分析,由平衡知识可知:2Ncos45°=mg,解得 N= mg,则正方体 2 对 1 的压力大小为 mg,选项 A 正确;由几何关系可知,正方体 2 落地前下落的 高度总等于正方体 1 向左移动的距离,可知正方体 2 落地前的速度与正方体 1 的速度总是大 小相等,选项 B 正确;正方体 2 落地前,1、2、3 构成的系统由于只有 2 的重力做功,则系统的机 械能守恒,选项 C 错误;正方体 2 落地前,1、2、3 构成的系统水平方向受合外力为零,则水平方 向动量守恒,选项 D 错误。 9.某同学用如图所示的装置“验证动量守恒定律”,其操作步骤如下: - 5 - A.将操作台调为水平; B.用天平测出滑块 A、B 的质量 mA、mB; C.用细线将滑块 A、B 连接,滑块 A、B 紧靠在操作台边缘,使 A、B 间的弹簧处于压缩状态; D.剪断细线,滑块 A、B 均做平抛运动,记录 A、B 滑块的落地点 M、N; E.用刻度尺测出 M、N 距操作台边缘的水平距离 x1、x2; F.用刻度尺测出操作台台面距地面的高度 h。 (1)上述步骤中,多余的步骤是__。 (2)如果动量守恒,须满足的关系是____(用测量量表示)。 【解析】取滑块 A 的初速度方向为正方向,两滑块的质量和平抛初速度大小分别为 mA、mB、v1、 v2,平抛运动的水平位移大小分别为 x1、x2,平抛运动的时间为 t。需要验证的方程为 0=mAv1-mBv2,又 v1= ,v2= ,代入得到 mAx1=mBx2,故不需要用刻度尺测出操作台台面距地面的 高度 h。所以多余的步骤是 F。 答案:(1)F　(2)mAx1=mBx2 10.如图所示,长 R=0.6m 的不可伸长的细绳一端固定在 O 点,另一端系着质量 m2=0.1kg 的小球 B,小球 B 刚好与水平面相接触。现使质量 m1=0.3 kg 的物块 A 沿光滑水平面以 v0=4 m/s 的速度 向 B 运动并与 B 发生弹性正碰,A、B 碰撞后,小球 B 能在竖直平面内做圆周运动,已知重力加速 度 g 取 10 m/s2,A、B 均可视为质点,试求: (1)在 A 与 B 碰撞后瞬间,小球 B 的速度 v2 的大小。 (2)小球 B 运动到最高点时对细绳的拉力大小。 【解析】(1)物块 A 与小球 B 碰撞时,由动量守恒定律和机械能守恒定律有:m1v0= m1v1+m2v2 m1 = m1 + m2 - 6 - 解得碰撞后瞬间物块 A 的速度 v1=2 m/s 小球 B 的速度 v2=6 m/s (2)碰撞后,设小球 B 运动到最高点时的速度为 v,则由机械能守恒定律有: m2 = m2v2+2m2gR 又由向心力公式有:Fn=F+m2g=m2 由牛顿第三定律得小球 B 对细绳的拉力大小 F′=F=1 N。 答案:(1)6 m/s　(2)1 N 【加固训练】 　　如图所示,在水平光滑直导轨上,静止着三个质量为 m=1 kg 的相同的小球 A、B、C。现让 A 球以 v0=2 m/s 的速度向 B 球运动,A、B 两球碰撞后粘在一起向右运动并与 C 球碰撞,C 球的最 终速度 vC=1 m/s。问: (1)A、B 两球与 C 球相碰前的共同速度多大? (2)两次碰撞过程中一共损失了多少动能? 【解析】(1)A、B 两球相碰,满足动量守恒定律,则有 mv0=2mv1 代入数据求得 A、B 两球跟 C 球相碰前的速度 v1=1 m/s (2)A、B 两球与 C 球碰撞同样满足动量守恒定律,则有 2mv1=mvC+2mv2 相碰后 A、B 两球的速度 v2=0.5 m/s 两次碰撞损失的动能 ΔEk= m - (2m) - m =1.25 J 答案:(1)1 m/s　(2)1.25 J 11.(2019·宁波模拟)在如图所示的足够长的光滑水平面上,有质量分别为 3 kg 和 1 kg 的甲、 乙两滑块,仅与甲拴接的轻弹簧压紧后处于静止状态。乙的右侧有一挡板 P。现将两滑块由静 止释放,当弹簧恢复原长时,甲的速度大小为 2 m/s,此时乙尚未与 P 相撞。 - 7 - (1)求弹簧恢复原长时乙的速度大小; (2)若乙与挡板 P 碰撞反弹后,不能再与弹簧发生碰撞,求挡板 P 对乙的冲量的最大值。 【解析】(1)当弹簧恢复原长时,设甲、乙的速度分别为 v1 和 v2,对两滑块及弹簧组成的系统, 设向左的方向为正方向,由动量守恒定律可得: m1v1+m2v2=0 又知 v1=2 m/s 联立以上方程可得 v2=-6 m/s,方向向右。 (2)乙反弹后甲、乙刚好不发生碰撞,则说明乙反弹的速度最大为 v3=2 m/s 由动量定理可得,挡板对乙滑块冲量的最大值为: I=m2v3-m2v2=1×2 N·s-1×(-6) N·s=8 N·s 答案:(1)6 m/s　(2)8 N·s 12.如图甲所示,两条相距 l 的光滑平行金属导轨位于同一竖直面(纸面)内,其上端接一阻值 为 R 的电阻;在两导轨间 OO′下方区域内有垂直导轨平面向里的匀强磁场,磁感应强度为 B。 现使电阻为 r、质量为 m 的金属棒 ab 由静止开始自 OO′位置释放,向下运动距离 d 后速度不 再变化。(棒 ab 与导轨始终保持良好的接触且下落保持水平,导轨电阻不计) (1)求棒 ab 在向下运动距离 d 过程中回路产生的总焦耳热。 (2)棒 ab 从静止释放经过时间 t0 下降了 ,求此时刻的速度大小。 (3)如图乙在 OO′上方区域加一面积为 S 的垂直于纸面向里的均匀磁场 B′,棒 ab 由静止开 始自 OO′上方某一高度处释放,自棒 ab 运动到 OO′位置开始计时,B′随时间 t 的变化关系 为 B′=kt,式中 k 为已知常量;棒 ab 以速度 v0 进入 OO′下方磁场后立即施加一竖直外力使其 保持匀速运动。求在 t 时刻穿过回路的总磁通量和电阻 R 的电功率。 - 8 - 【解析】(1)对闭合回路:I= 对 ab 棒,由平衡知识可知:mg=BIl 解得 vm= 由能量关系:mgd= m +Q 解得 Q=mgd- (2)由动量定理可知:(mg-BIl)t0=mv 即 mgt0-Blq=mv 由 q= 解得 v=gt0- (3)因为:Φ=Blv0t+ktS 由法拉第电磁感应定律可得:E= =Blv0+kS I= ,P=I2R 解得 P= R 答案:(1)mgd- (2)gt0- (3)Blv0t+ktS　 R