广东省2021高考物理一轮复习专题五万有引力与航天课件 46页

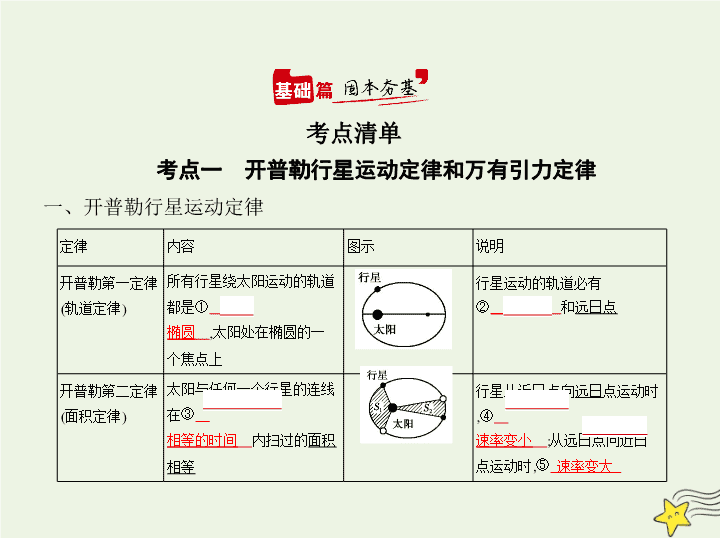
考点一　开普勒行星运动定律和万有引力定律 一、开普勒行星运动定律 考点清单 定律 内容 图示 说明 开普勒第一定律(轨道定律) 所有行星绕太阳运动的轨道都是① 　椭圆     ,太阳处在椭圆的一个焦点上   行星运动的轨道必有 ② 　近日点     和 远日点 开普勒第二定律(面积定律) 太阳与任何一个行星的连线在③ 　相等的时间     内扫过的 面积相等   行星从 近日 点向 远日 点运动时,④ 　速率变小     ;从远日点向近日点运动时,⑤ 速率变大   开普勒第三定律(周期 定律) 所有行星的轨道半长轴 r 的三次方与其公转周期 T 的二次方的比值 都相等,即⑥      r 3 / T 2 = k        比值 k 只与被环绕天体 有关,与行星无关 二、万有引力定律 考点二　天体运动与人造卫星 1.三种宇宙速度   3.极地卫星和近地卫星 (1)极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实 现全球覆盖。 2.同步卫星的六个“一定” (2)近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫星,其运行的 轨道半径可近似认为等于 地球的半径 ,其运行线速度约为7.9 km/s。 思考 :1969 年 7 月 20 日 , 美国宇航员阿姆斯特朗在月球上留下了人类第一只脚印 , 迈出了人类征服宇宙的一大步。 探讨 1: 宇航员在月球上用弹簧测力计测出质量为 m 的物体重力为 F, 怎样利用这个条件估测月球的质量 ? 提示 : 设月球质量为 M 、半径为 R, 则 F=G   , 故 M=  。 探讨 2: 宇航员驾驶指令舱绕月球表面飞行一周的时间为 T, 怎样利用这个条件估测月球质量 ? 提示 : 设月球质量为 M 、半径为 R, 由万有引力提供向心力 ,G   =m   R, 得 M=  。 拓展一　开普勒行星运动定律及其理解 1.开普勒第一定律 (1)认识:尽管各行星的轨道半径不同,但它们的共同规律是所有行星都沿 椭圆轨道绕太阳运动,太阳则位于所有椭圆的一个焦点上。 (2)意义:否定了行星运动轨道为圆形的说法,建立了正确的轨道理论,给出 了太阳准确的位置。 2.开普勒第二定律 (1)认识:行星靠近太阳时速度增大,远离太阳时速度减小。近日点速度最 大,远日点速度最小。 知能拓展 (2) 意义 : 描述了行星在其轨道上运行时 , 线速度的大小不断变化 , 并阐明了 速度大小变化的数量关系。 3. 开普勒第三定律 (1)认识:它揭示了周期与轨道半长轴之间的关系,椭圆轨道半长轴越长的 行星,其公转周期越大;反之,其公转周期越小。 (2)意义:比例常数 k 与行星无关,只与太阳有关。 例1    (2019河南三模,15,6分)“嫦娥五号”月球探测器预计在2019年年底 发射,采集月球样品并返回地球,全面实现月球探测工程“三步走”战略目 标。若“嫦娥五号”在距月球表面 H 处的环月轨道Ⅰ上做匀速圆周运动, 其运行的周期为 T ;随后“嫦娥五号”在该轨道上某点采取措施,降至椭圆 轨道Ⅱ上,如图所示。若近月点接近月球表面,而 H 等于月球半径,忽略月球 自转及地球对它的影响,则“嫦娥五号”在轨道Ⅱ上的运行周期为   (    　) A.   T 　　　    B.   T 　　　    C.   T 　　　    D.   T 解析　在Ⅰ轨道上,轨道半径 r 1 = R + H =2 R ,在Ⅱ轨道上,半长轴为 a =   =   R ,根据开普勒第三定律知   =   ,解得 T 2 =   T ,故选项C正确。 答案    C 拓展二　万有引力与重力的关系 1.万有引力与重力的关系 地球对地面上的物体的万有引力 F 表现为两个效果:其中一个分力等于重 力 mg ,另一个分力提供物体随地球自转的向心力 F 向 。 (1)在赤道处: G   = mg 1 + mω 2 R 。 (2)在两极处: G   = mg 0 。 (3)在一般位置:万有引力 F 等于重力 mg 与向心力 F 向 的矢量和。 越靠近南、北两极, g 值越大,由于物体随地球自转所需的向心力较小,常认 为万有引力近似等于重力,即   = mg 。 2.星球上空的重力加速度 g ' 星球上空距离星球中心 r = R + h 处的重力加速度为 g ', mg '=   ,得 g '=   ,所以   =   。 3.万有引力的“两点理解”和“两个推论” (1)两点理解 ①两物体间相互作用的万有引力是一对作用力和反作用力。 ②地球上的物体(两极除外)受到的重力只是万有引力的一个分力。 (2)两个推论 ①推论1:在匀质球壳的空腔内任意位置处,质点受到球壳的万有引力的合 力为零,即∑ F 引 =0。 ②推论2:在匀质球体内部距离球心 r 处的质点( m )受到的万有引力等于球体 内半径为 r 的同心球体( M ')对其的万有引力,即 F = G   。 例2　已知质量分布均匀的球壳对壳内物体的引力为0。假设地球是一半 径为 R 的质量分布均匀的球体,地球表面的重力加速度大小为 g 。试求: (1)在地面上方离地面距离为   处的重力加速度大小与在地面下方地球内 部离地面距离为   处的重力加速度大小之比; (2)设想地球的密度不变,自转周期不变,但地球球体半径变为原来的一半, 仅考虑地球和同步卫星之间的相互作用力,则该“设想地球”的同步卫星 的轨道半径与以前地球的同步卫星的轨道半径的比值。 解析　(1)由万有引力等于重力知   = mg 1   = mg 2 且有   =   =   则   =   (2)地球对同步卫星的万有引力提供同步卫星转动的向心力   = m '   r 1   = m '   r 2 M = ρ ·   π R 3 M 1 = ρ ·   π   解得   =   答案　(1)8∶9　(2)   拓展三　天体质量和密度的计算 方法 已知量 利用公式 表达式 备注 质量的计算 利用运行天体 r 、 T G   = mr   M =   只能得到 中心天体 的质量     r 、 v G   = m   M =   v 、 T G   = m   G   = mr   M =   利用天体表面 重力加速度 g 、 R mg =   M =   — 密度的计算 利用运 行天体 r 、 T 、 R G   = mr   M = ρ ·   π R 3 ρ =   当 r = R 时 ρ =   利用近地 卫星只需 测出其运 行周期     利用天体 表面重力 加速度     g 、 R mg =   M = ρ ·   π R 3 ρ =   — 例3　1789年英国物理学家卡文迪许测出引力常量 G ,因此卡文迪许被人们 称为“能称出地球质量的人”。若已知引力常量为 G ,地球表面处的重力 加速度为 g ,地球半径为 R ,地球上一个昼夜的时间为 T 1 (地球自转周期),一年 的时间为 T 2 (地球公转周期),地球中心到月球中心的距离为 L 1 ,地球中心到 太阳中心的距离为 L 2 。下列说法正确的是   (　　) A.地球的质量 m 地 =   B.太阳的质量 m 太 =   C.月球的质量 m 月 =   D.由题中数据可求月球的密度 解析　若不考虑地球自转,根据地球表面万有引力等于重力,有 G   = mg , 则 m 地 =   ,故A错误;根据太阳对地球的万有引力提供向心力,有 G   = m 地   L 2 ,则 m 太 =   ,故B正确;由题中数据无法求出月球的质量,也无法求 出月球的密度,故C、D错误。 答案    B 拓展四　人造卫星运行轨道与参量的分析 1.人造卫星的轨道:卫星绕地球做匀速圆周运动时,由地球对它的万有引力 提供向心力。因此卫星绕地球做匀速圆周运动的圆心必与地心重合,而这 样的轨道有多种,其中比较特殊的有与赤道共面的赤道轨道和通过两极点 上空的极地轨道。当然也存在着与赤道平面呈某一角度的圆轨道。 人造地球卫星的三种轨道   2.卫星的线速度、角速度、周期、向心加速度与轨道半径的关系 做匀速圆周运动的卫星所受万有引力完全提供其所需向心力,由 G   = m   = mω 2 r = m   r = ma 可推导出:   ⇒ 当 r 增大时   例4　地球赤道上有一物体随地球自转而做圆周运动,所受到的向心力为 F 1 ,向心加速度为 a 1 ,线速度为 v 1 ,角速度为 ω 1 ;绕地球表面附近做圆周运动的 人造卫星(高度忽略)所受到的向心力为 F 2 ,向心加速度为 a 2 ,线速度为 v 2 ,角 速度为 ω 2 ;地球同步卫星所受到的向心力为 F 3 ,向心加速度为 a 3 ,线速度为 v 3 , 角速度为 ω 3 。假设三者质量相等,地球表面的重力加速度为 g ,第一宇宙速 度为 v ,则   (　　) A. F 1 = F 2 > F 3 　    B. a 1 = a 2 = g > a 3 C. v 1 = v 2 = v > v 3 　    D. ω 1 = ω 3 < ω 2 解析　根据题意,研究对象三者质量相等,轨道半径 r 1 = r 2 < r 3 。物体与人造卫 星比较,由于赤道上物体受引力和支持力的合力提供向心力,而人造卫星只 受万有引力,故 F 1 < F 2 ,故A错误;由选项A的分析知道向心力 F 1 < F 2 ,故由牛顿 第二定律可知 a 1 < a 2 ,故B错误;由A选项的分析知道向心力 F 1 < F 2 ,根据向心力 公式 F = m   , m 、 R 相等,故 v 1 < v 2 ,故C错误;地球同步卫星与地球自转同步,故 T 1 = T 3 ,地球同步卫星轨道半径比人造卫星轨道半径大,根据周期公式 T =2π   可知, T 3 > T 2 ,再根据 ω =   ,有 ω 1 = ω 3 < ω 2 ,故D正确。 答案    D 方法技巧 　天体运动的分析与计算 1.基本思路:一般行星或卫星的运动可看作匀速圆周运动,所需向心力由中 心天体对它的万有引力提供。 2.常用关系: (1) G   = ma = m   = mω 2 r = m   r 。 (2)忽略自转时, mg = G   (物体在天体表面时受到的万有引力等于物体重 力),整理可得: gR 2 = GM ,该公式通常被称为“黄金代换式”。 拓展五　宇宙速度及其理解 1.第一宇宙速度 (1)认识:第一宇宙速度是人造卫星近地环绕地球做匀速圆周运动必须具备 的速度,即近地卫星的环绕速度。 (2)推导:对于近地人造卫星,轨道半径 r 近似等于地球半径 R =6 400 km,卫星 在轨道处所受的万有引力近似等于卫星在地面上所受的重力,取 g =9.8 m/s 2 , 则 方法一:   方法二:   (3)决定因素:由第一宇宙速度的计算式 v =   可以看出,第一宇宙速度的 值由中心天体决定,第一宇宙速度的大小取决于中心天体的质量 M 和半径 R ,与卫星无关。 (4)对发射速度和环绕速度的理解 ①“最小发射速度”:近地轨道是人造卫星的最低运行轨道,而近地轨道的 发射速度就是第一宇宙速度,所以第一宇宙速度是发射人造卫星的最小速 度。 ②“最大环绕速度”:在所有环绕地球做匀速圆周运动的卫星中,近地卫星 的轨道半径最小,线速度越大,所以在这些卫星中,近地卫星的线速度即第 一宇宙速度是最大环绕速度。 2.宇宙速度与运动轨迹的关系 (1) v 发 =7.9 km/s时,卫星绕地球做匀速圆周运动。 (2)7.9 km/s< v 发 <11.2 km/s,卫星绕地球运动的轨迹为椭圆。 (3)11.2 km/s ≤ v 发 <16.7 km/s,卫星绕太阳做椭圆运动。 (4) v 发 ≥ 16.7 km/s,卫星将挣脱太阳引力的束缚,飞到太阳系以外的空间。 例5　我国的火星探测任务基本确定,将于2020年发射火星探测器。已知 火星的质量约为地球质量的   ,火星的半径约为地球半径的   。下列关于 火星探测器的说法中正确的是   (　　) A.发射速度只要大于第一宇宙速度即可 B.发射速度只有达到第三宇宙速度才可以 C.发射速度应大于第二宇宙速度且小于第三宇宙速度 D.火星探测器环绕火星运行的最大速度约为地球的第一宇宙速度的   解析　要将火星探测器发射到火星上去,必须脱离地球引力,即发射速度要 大于第二宇宙速度,火星探测器仍在太阳系内运行,因此从地球上发射时, 发射速度要小于第三宇宙速度,A、B错误,C正确;由第一宇宙速度的概念, 得 G   = m   ,解得 v =   ,故火星探测器环绕火星运行的最大速度与地 球的第一宇宙速度之比为   =   ·   =   =   ,D正确。 答案    CD 拓展六　卫星与宇宙飞船的变轨问题 1.卫星的变轨问题 卫星变轨时,先是线速度 v 发生变化导致需要的向心力发生变化,进而使轨 道半径 r 发生变化。   (1)当卫星减速时,卫星所需的向心力 F 向 = m   减小,万有引力大于所需的向 心力,卫星将做近心运动,向低轨道变迁。 (2)当卫星加速时,卫星所需的向心力 F 向 = m   增大,万有引力不足以提供卫 星所需的向心力,卫星将做离心运动,向高轨道变迁。 以上两点是比较椭圆和圆轨道切点速度的依据。 2.飞船对接问题 (1)低轨道飞船与高轨道空间站对接如图甲所示,低轨道飞船通过合理地加 速,沿椭圆轨道(做离心运动)追上高轨道空间站与其完成对接。   (2)同一轨道飞船与空间站对接 如图乙所示,后面的飞船先减速降低高度,再加速提升高度,通过适当控制, 使飞船追上空间站时恰好具有相同的速度。 3.卫星轨道的突变 由于技术上的需要,有时要在适当的位置短时间内启动飞行器上的发动机, 使飞行器轨道发生突变,使其进入预定的轨道。如图所示,发射同步卫星 时,可以分多过程完成:   (1)先将卫星发送到近地轨道Ⅰ。 (2)使其绕地球做匀速圆周运动,速率为 v 1 ,变轨时在 P 点点火加速,短时间内 速率由 v 1 增加到 v 2 ,使卫星进入椭圆形的转移轨道Ⅱ。 (3)卫星运行到远地点 Q 时的速率为 v 3 ,此时进行第二次点火加速,在短时间 内速率由 v 3 增加到 v 4 ,使卫星进入同步轨道Ⅲ,绕地球做匀速圆周运动。 例6　如图所示为卫星发射过程的示意图,先将卫星发射至近地圆轨道1,然 后点火,使其沿椭圆轨道2运行,最后再一次点火,将卫星送入同步圆轨道 3。轨道1、2相切于 Q 点,轨道2、3相切于 P 点,则当卫星分别在1、2、3轨 道上正常运行时,以下说法正确的是(　　)   A.卫星在轨道3上的速率大于在轨道1上的速率 B.卫星在轨道3上的周期大于在轨道2上的周期 C.卫星在轨道1上经过 Q 点时的速率大于它在轨道2上经过 Q 点时的速率 D.卫星在轨道2上经过 P 点时的加速度小于它在轨道3上经过 P 点时的加速 度 解析　卫星在圆轨道上做匀速圆周运动时有: G   = m   , v =   ,因为 r 1 < r 3 ,所以 v 1 > v 3 ,A项错误;由开普勒第三定律知 T 3 > T 2 ,B项正确;卫星在 Q 点从轨 道1到轨道2需要做离心运动,故需要加速,在 Q 点   >   ,C项错误;在同一点 P ,由   = ma 知,卫星在轨道2上经过 P 点时的加速度等于它在轨道3上经 过 P 点时的加速度,D项错误。 答案    B 应用一　“赤道上物体”“同步卫星”和“近地卫星”的比较 实践探究 1.同步卫星和近地卫星 相同点:都是万有引力提供向心力,即都满足   = m   = mω 2 r = m   r = ma 。 由上式比较各物理量的关系, r 越大, v 、 ω 、 a 越小, T 越大。 2.同步卫星和赤道上物体 相同点:周期和角速度相同。 不同点:向心力来源不同。   = ma = mω 2 r 只对同步卫星成立。 对于赤道上物体,有   = mg + mω 2 r 。 因此要通过 v = ωr , a = ω 2 r 比较两者的线速度和向心加速度的大小关系。 例1　如图所示,同步卫星与地心的距离为 r ,运行速率为 v 1 ,向心加速度为 a 1 , 地球赤道上的物体随地球自转的向心加速度为 a 2 ,第一宇宙速度为 v 2 ,地球 半径为 R ,则下列比值正确的是(　　)   A.   =   　    B.   =(   ) 2 C.   =   　    D.   =   解析　地球同步卫星:轨道半径为 r ,运行速率为 v 1 ,向心加速度为 a 1 ;地球赤 道上的物体:轨道半径为 R ,随地球自转的向心加速度为 a 2 ;以第一宇宙速度 运行的卫星为近地卫星,其轨道半径为 R 。对于卫星,其共同特点是万有引 力提供向心力,则 G   = m   ,故   =   。对于同步卫星和地球赤道上的物 体,其共同特点是角速度相等,由 a = ω 2 r ,得   =   。故选A、D。 答案    AD 应用二　多星系统模型 实践探究 在天体运动中彼此相距较近,在相互间的万有引力作用下,围绕同一点 做匀速圆周运动的星体系统称为宇宙多星模型。 “双星”模型 “三星”模型 “四星”模型 情景 图           运动 特点 转动方向、周期、角 速度相同,运动半径一 般不等 转动方向、周期、角 速度、线速度大小均 相同,圆周运动半径相 等 转动方向、周期、角 速度、线速度大小均 相同,圆周运动半径相 等 受力 特点 两星间的万有引力提 供各星做匀速圆周运 动的向心力 每颗星所受万有引力 的合力提供各星做匀 速圆周运动的向心力 每颗星所受万有引力 的合力提供各星做匀 速圆周运动的向心力 规律   = m 1 ω 2 r 1   = m 2 ω 2 r 2   +   = ma 向 ,   × cos 30 °× 2= ma 向   × 2 cos 45 ° +   = ma 向 ,   × 2 × cos 30 ° +   = ma 向 关键 点 m 1 r 1 = m 2 r 2 , r 1 + r 2 = L r 2 =   r 1 =   L , r 2 =   例2　两个靠得很近的天体,离其他天体非常遥远,它们以其连线上某一点 O 为圆心各自做匀速圆周运动,两者的距离保持不变,科学家把这样的两个 天体称为“双星”,如图所示。已知双星的质量分别为 m 1 和 m 2 ,它们之间的 距离为 L ,引力常量为 G ,求双星的运行轨道半径 r 1 和 r 2 及运行周期 T 。   解析　双星间的万有引力提供各自做圆周运动的向心力 对 m 1 :   = m 1 r 1 ω 2 , 对 m 2 :   = m 2 r 2 ω 2 , 且 r 1 + r 2 = L , 解得 r 1 =   , r 2 =   。 由 G   = m 1 r 1   及 r 1 =   得 周期 T =   。 答案                     应用三　天体的追及、相遇问题 实践探究 1.相距最近 两天体的运转轨道在同一平面内,则两天体与中心天体在同一直线上,且位 于中心天体同侧时,两天体相距最近,从运动关系上,两天体运动关系应满 足( ω A - ω B ) t =2 n π( n =1,2,3, … )。 2.相距最远 两天体的运转轨道在同一平面内,则两天体与中心天体在同一直线上,且位 于中心天体异侧时,两天体相距最远,从运动关系上,两天体运动关系应满 足( ω A - ω B ) t '=(2 n -1)π( n =1,2,3, … )。 例3　当地球位于太阳和木星之间且三者几乎排成一条直线时,称之为 “木星冲日”,2019年6月10日出现了一次“木星冲日”。已知木星与地 球几乎在同一平面内沿同一方向绕太阳近似做匀速圆周运动,木星到太阳 的距离大约是地球到太阳距离的5倍。则下列说法正确的是   (　　) A.下一次的“木星冲日”时间肯定在2021年 B.下一次的“木星冲日”时间肯定在2020年 C.木星运行的加速度比地球运行的加速度大 D.木星运行的周期比地球运行的周期小 解析　木星和地球都绕太阳做圆周运动,都是万有引力提供向心力,故加速 度 a =   =   ,木星到太阳的距离大约是地球到太阳距离的5倍,故木星运行 的加速度比地球运行的加速度小,故C错误;万有引力提供向心力,由   = m   r ,得 T =2π   ,木星到太阳的距离大约是地球到太阳距离的5倍,地 球公转周期为 T 1 =1年,那么木星公转周期为 T 2 =   T 1 ≈ 11.2 T 1 =11.2年;设 “木星冲日”的周期为 T ',则有   -   =1,解得 T '=   ≈   年 ≈ 1.1年,因20 19年6月10日出现了一次“木星冲日”,下一次的“木星冲日”时间肯定 在2020年,故A、D错误,B正确。 答案    B