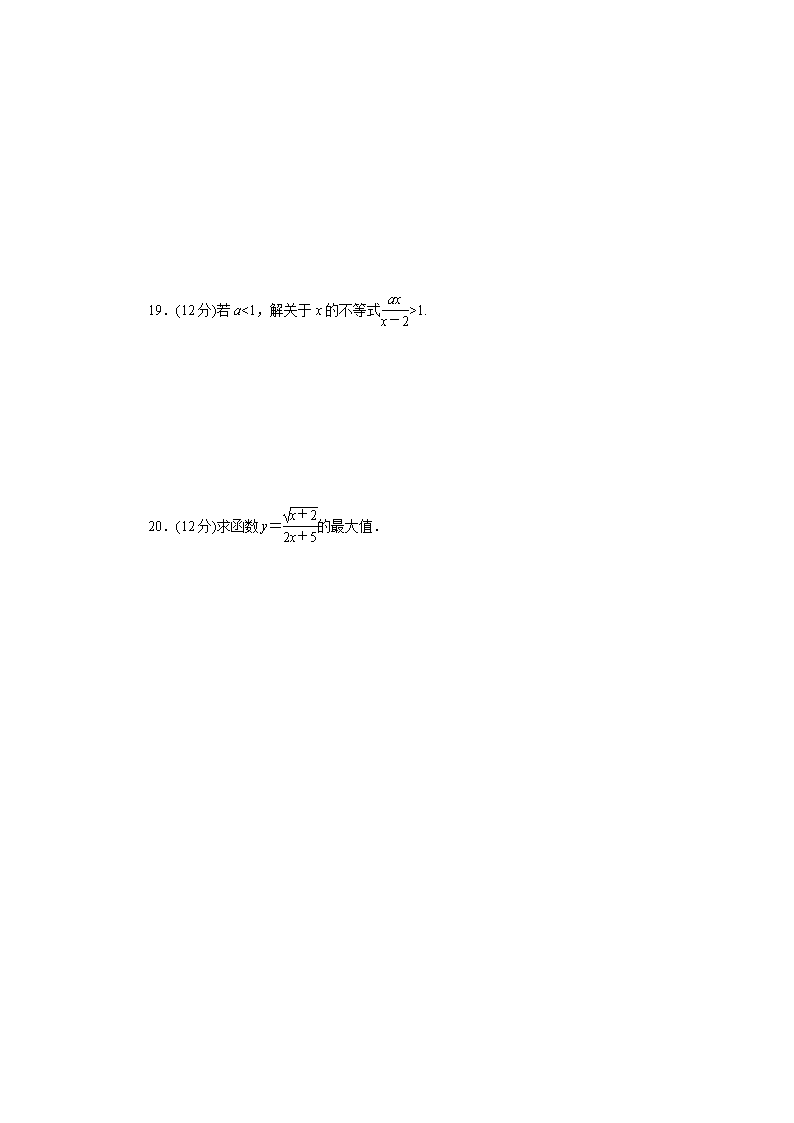1. 您所在位置：首页 > 中小学教育 > 高中教育 > 教案 > 高二数学人教a必修5练习：第三章不等式章末检测（b）word版含解析

高二数学人教a必修5练习：第三章不等式章末检测（b）word版含解析 8页

  • 107.22 KB
  • 2021-06-09 发布

高二数学人教a必修5练习：第三章不等式章末检测（b）word版含解析

  • 8页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
  4. 网站客服QQ：403074932
第三章 章末检测(B) (时间：120 分钟 满分：150 分) 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分) 1．若 a<0，－1ab>ab2 B．ab2>ab>a C．ab>a>ab2 D．ab>ab2>a 2．已知 x>1，y>1，且 1 4ln x，1 4 ，ln y 成等比数列，则 xy( ) A．有最大值 e B．有最大值 e C．有最小值 e D．有最小值 e 3．设 M＝2a(a－2)，N＝(a＋1)(a－3)，则( ) A．M>N B．M≥N C．Mb，则下列不等式中恒成立的是( ) A．a2>b2 B．(1 2)a<(1 2)b C．lg(a－b)>0 D.a b>1 6．当 x>1 时，不等式 x＋ 1 x－1 ≥a 恒成立，则实数 a 的取值范围是( ) A．(－∞，2] B．[2，＋∞) C．[3，＋∞) D．(－∞，3] 7．已知函数 f(x)＝ x＋2， x≤0 －x＋2， x>0 ，则不等式 f(x)≥x2 的解集是( ) A．[－1,1] B．[－2,2] C．[－2,1] D．[－1,2] 8．若 a>0，b>0，且 a＋b＝4，则下列不等式中恒成立的是( ) A. 1 ab>1 2 B.1 a ＋1 b ≤1 C. ab≥2 D. 1 a2＋b2 ≤1 8 9．设变量 x，y 满足约束条件 x－y≥0， 2x＋y≤2， y＋2≥0， 则目标函数 z＝|x＋3y|的最大值为( ) A．4 B．6 C．8 D．10 10．甲、乙两人同时从寝室到教室，甲一半路程步行，一半路程跑步，乙一半时间步行， 一半时间跑步，如果两人步行速度、跑步速度均相同，则( ) A．甲先到教室 B．乙先到教室 C．两人同时到教室 D．谁先到教室不确定 11．设 M＝ 1 a －1 1 b －1 1 c －1 ，且 a＋b＋c＝1 (其中 a，b，c 为正实数)，则 M 的取值 范围是( ) A. 0，1 8 B. 1 8 ，1 C．[1,8) D．[8，＋∞) 12．函数 f(x)＝x2－2x＋ 1 x2－2x＋1 ，x∈(0,3)，则( ) A．f(x)有最大值7 4 B．f(x)有最小值－1 C．f(x)有最大值 1 D．f(x)有最小值 1 题 号 1 2 3 4 5 6 7 8 9 10 11 12 答 案 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分) 13．已知 t>0，则函数 y＝t2－4t＋1 t 的最小值为 ________________________________________________________________________． 14．对任意实数 x，不等式(a－2)x2－2(a－2)x－4<0 恒成立，则实数 a 的取值范围是 ________． 15．若不等式组 x－y＋5≥0， y≥a， 0≤x≤2 表示的平面区域是一个三角形，则 a 的取值范围是 ________． 16．某公司一年购买某种货物 400 吨，每次都购买 x 吨，运费为 4 万元/次，一年的总 存储费用为 4x 万元，要使一年的总运费与总存储费用之和最小，则 x＝________吨． 三、解答题(本大题共 6 小题，共 70 分) 17．(10 分)已知 a>0，b>0，且 a≠b，比较a2 b ＋b2 a 与 a＋b 的大小． 18．(12 分)已知 a，b，c∈(0，＋∞)． 求证：( a a＋b )·( b b＋c )·( c c＋a )≤1 8. 19．(12 分)若 a<1，解关于 x 的不等式 ax x－2 >1. 20．(12 分)求函数 y＝ x＋2 2x＋5 的最大值． 21．(12 分)如图所示，将一矩形花坛 ABCD 扩建成一个更大的矩形花坛 AMPN，要求 B 点在 AM 上，D 点在 AN 上，且对角线 MN 过 C 点，已知 AB＝3 米，AD＝2 米． (1)要使矩形 AMPN 的面积大于 32 平方米，则 DN 的长应在什么范围内？ (2)当 DN 的长为多少时，矩形花坛 AMPN 的面积最小？并求出最小值． 22．(12 分)某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、 劳动力、获得利润及每天资源限额(最大供应量)如表所示： 产品消耗量资源 甲产品 (每吨) 乙产品 (每吨) 资源限额 (每天) 煤(t) 9 4 360 电力(kw· h) 4 5 200 劳动力(个) 3 10 300 利润(万元) 6 12 问：每天生产甲、乙两种产品各多少吨时，获得利润总额最大？ 第三章 不等式 章末检测答案(B) 1．D [∵a<0，－10，ab2<0. ∴ab>a，ab>ab2. ∵a－ab2＝a(1－b2)＝a(1＋b)(1－b)<0， ∴a0.∴M>N.] 4．B [∵x2－ax－12a2<0(a<0) ⇔(x－4a)(x＋3a)<0 ⇔4a1，∴x＋ 1 x－1 ＝(x－1)＋ 1 x－1 ＋1≥ 2 x－1· 1 x－1 ＋1＝3.∴a≤3.] 7．A [f(x)≥x2⇔ x≤0 x＋2≥x2 或 x>0 －x＋2≥x2 ⇔ x≤0 x2－x－2≤0 或 x>0 x2＋x－2≤0 ⇔ x≤0 －1≤x≤2 或 x>0 －2≤x≤1 ⇔－1≤x≤0 或 00， 故选 B.] 11．D [M＝ 1 a －1 1 b －1 1 c －1 ＝ a＋b＋c a －1 a＋b＋c b －1 a＋b＋c c －1 ＝ b a ＋c a · a b ＋c b · a c ＋b c ≥2 b a·c a·2 a b·c b·2 a c·b c ＝8. ∴M≥8，当 a＝b＝c＝1 3 时取“＝”．] 12．D [∵x∈(0,3)，∴x－1∈(－1,2)， ∴(x－1)2∈[0,4)， ∴f(x)＝(x－1)2＋ 1 x－12 －1 ≥2 x－12· 1 x－12 －1＝2－1＝1. 当且仅当(x－1)2＝ 1 x－12 ，且 x∈(0,3)， 即 x＝2 时取等号，∴当 x＝2 时，函数 f(x)有最小值 1.] 13．－2 解析 ∵t>0， ∴y＝t2－4t＋1 t ＝t＋1 t －4≥2－4＝－2. 14．－20，b>0，a≠b， ∴(a－b)2>0，a－b>0，ab>0， ∴(a2 b ＋b2 a )－(a＋b)>0，∴a2 b ＋b2 a >a＋b. 18．证明 ∵a，b，c∈(0，＋∞)， ∴a＋b≥2 ab>0，b＋c≥2 bc>0， c＋a≥2 ac>0， ∴(a＋b)(b＋c)(c＋a)≥8abc>0. ∴ abc a＋bb＋cc＋a ≤1 8 即( a a＋b)·( b b＋c)·( c c＋a)≤1 8. 当且仅当 a＝b＝c 时，取到“＝”． 19．解 不等式 ax x－2>1 可化为a－1x＋2 x－2 >0. ∵a<1，∴a－1<0， 故原不等式可化为 x－ 2 1－a x－2 <0. 故当 00 时，y＝ 1 2t＋1 t ≤ 1 2 2t·1 t ＝ 2 4 . 当且仅当 2t＝1 t ，即 t＝ 2 2 时等号成立． 即当 x＝－3 2 时，ymax＝ 2 4 . 21．解 (1)设 DN 的长为 x(x>0)米， 则 AN＝(x＋2)米． ∵DN AN ＝DC AM ，∴AM＝3x＋2 x ， ∴SAMPN＝AN·AM＝3x＋22 x ， 由 SAMPN>32，得3x＋22 x >32. 又 x>0，得 3x2－20x＋12>0， 解得：06， 即 DN 长的取值范围是(0，2 3)∪(6，＋∞)． (2)矩形花坛 AMPN 的面积为 y＝3x＋22 x ＝3x2＋12x＋12 x ＝3x＋12 x ＋12≥2 3x·12 x ＋12＝24， 当且仅当 3x＝12 x ，即 x＝2 时， 矩形花坛 AMPN 的面积取得最小值 24. 故 DN 的长为 2 米时，矩形 AMPN 的面积最小， 最小值为 24 平方米． 22．解 设此工厂每天应分别生产甲、乙两种产品 x 吨、y 吨，获得利润 z 万元． 依题意可得约束条件： 9x＋4y≤360 4x＋5y≤200 3x＋10y≤300 x≥0 y≥0 作出可行域如图. 利润目标函数 z＝6x＋12y， 由几何意义知，当直线 l：z＝6x＋12y 经过可行域上的点 M 时，z＝6x＋12y 取最大值．解 方程组 3x＋10y＝300 4x＋5y＝200 ， 得 x＝20，y＝24，即 M(20,24)． 答 生产甲种产品 20 吨，乙种产品 24 吨，才能使此工厂获得最大利润．

您可能关注的文档

相关文档

最近下载