【新教材】2020-2021学年高中人教A版数学必修第二册习题：9-2-1　总体取值规律的估计　9-2 6页

‎9.2　用样本估计总体 ‎9.2.1　总体取值规律的估计　9.2.2　总体百分位数的估计 课后篇巩固提升 基础达标练 ‎1.某班学生在一次数学考试中各分数段以及人数的成绩分布为:[0,80),2人;[80,90),6人;[90,100),4人;[100,110),8人;[110,120),12人;[120,130),5人;[130,140),6人;[140,150),2人.则分数在[100,130)中的频数以及频率分别为(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A.25,0.56 B.20,0.56‎ C.25,0.50 D.13,0.29‎ 解析由题意知该班总人数为2+6+4+8+12+5+6+2=45,其中成绩在[100,130)的人数为8+12+5=25,故分数在[100,130)中的频数为25,频率为≈0.56.‎ 答案A ‎2.为了了解某学校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示.根据此图,估计该校2 000名高中男生中体重不小于70.5 kg的人数为(　　)‎ A.300 B.360‎ C.420 D.450‎ 解析由题中频率分布直方图,得这100名高中男生体重不小于70.5 kg的频率是(0.04+0.035+0.015)×2=0.18,所以估计该校2 000名高中男生中体重不小于70.5 kg的频率是0.18,则估计该校2 000名高中男生中体重不小于70.5 kg的人数为2 000×0.18=360.‎ 答案B ‎3.(多选题)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.‎ 根据该折线图,下列结论正确的是(　　)‎ A.年接待游客量逐年增加 B.月接待游客量逐月增加 C.各年的月接待游客量高峰期大致在7,8月 D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 解析在A中,年接待游客量逐年增加,故A正确;‎ 在B中,月接待游客量8月份后开始减少,虽有所反弹,但仍是减少的趋势,故B错误;‎ 在C中,各年的月接待游客量高峰期大致在7,8月,故C正确;‎ 在D中,各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D正确.‎ 答案ACD ‎4.如图是某学校学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为10,则抽取的学生人数是　　　　. ‎ 解析由图可得前3组的频率和为1-(0.037 5+0.012 5)×5=0.75,∴第2小组的频率为0.75×=0.25,∴抽取的学生人数是=40.‎ 答案40‎ ‎5.为了帮助班上的两名贫困生解决经济困难,班上的20名同学捐出了自己的零花钱.他们捐款数(单位:元)如下:19,20,25,30,24,23,25,29,27,27,28,28,26,27,21,30,20,19,22,20.班主任老师准备将这组数据制成频率分布直方图,以表彰他们的爱心.制图时先计算最大值与最小值的差是　　　　　.若取组距为2,则应分成　　　　　组;若第一组的起点定为18.5,则在[26.5,28.5)内的频数为　　　　　. 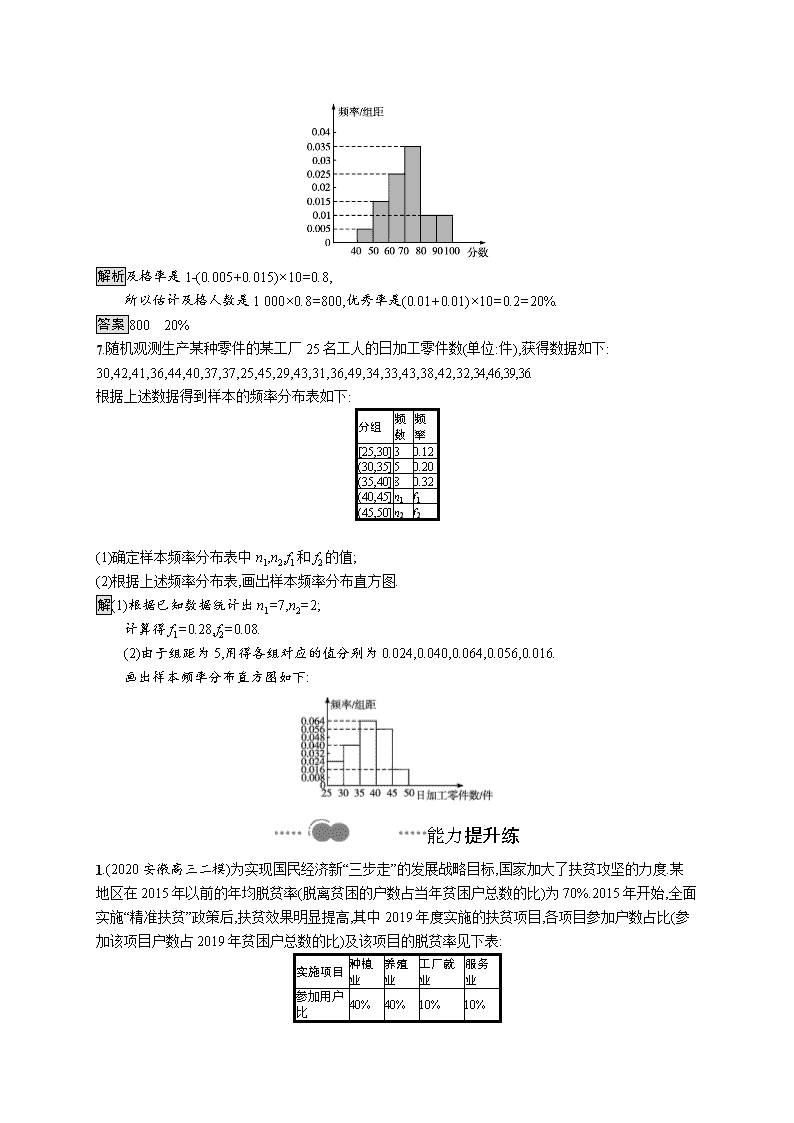‎ 解析由题意知,极差为30-19=11;因为组距为2,=5.5不是整数,所以取6组;捐款数落在[26.5,28.5)内的有27,27,28,28,27共5个,因此频数为5.‎ 答案11　6　5‎ ‎6.统计某校1 000名学生的数学测试成绩,得到样本的频率分布直方图如图所示,规定不低于60分为及格,不低于80分为优秀,则估计及格人数是　　　　　;优秀率是　　　　　. ‎ 解析及格率是1-(0.005+0.015)×10=0.8,‎ 所以估计及格人数是1 000×0.8=800,优秀率是(0.01+0.01)×10=0.2=20%.‎ 答案800　20%‎ ‎7.随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:‎ ‎30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.‎ 根据上述数据得到样本的频率分布表如下:‎ 分组 频数 频率 ‎[25,30]‎ ‎3‎ ‎0.12‎ ‎(30,35]‎ ‎5‎ ‎0.20‎ ‎(35,40]‎ ‎8‎ ‎0.32‎ ‎(40,45]‎ n1‎ f1‎ ‎(45,50]‎ n2‎ f2‎ ‎(1)确定样本频率分布表中n1,n2,f1和f2的值;‎ ‎(2)根据上述频率分布表,画出样本频率分布直方图.‎ 解(1)根据已知数据统计出n1=7,n2=2;‎ 计算得f1=0.28,f2=0.08.‎ ‎(2)由于组距为5,用得各组对应的值分别为0.024,0.040,0.064,0.056,0.016.‎ 画出样本频率分布直方图如下:‎ 能力提升练 ‎1.(2020安徽高三二模)为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为70%.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占2019年贫困户总数的比)及该项目的脱贫率见下表:‎ 实施项目 种植业 养殖业 工厂就业 服务业 参加用户比 ‎40%‎ ‎40%‎ ‎10%‎ ‎10%‎ 脱贫率 ‎95%‎ ‎95%‎ ‎90%‎ ‎90%‎ 那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的(　　)‎ A.倍 B.倍 C.倍 D.倍 解析设贫困户总数为a,脱贫率 p==94%,‎ 所以.故2019年的年均脱贫率是实施“精准扶贫”政策前的年均脱贫率的倍.‎ 答案B ‎2.(2019山东高三二模)港珠澳大桥于2018年10月24日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55 km.桥面为双向六车道高速公路,大桥通行限速100 km/h,现对大桥某路段上1 000辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图),根据直方图估计在此路段上汽车行驶速度在区间[85,90)内的车辆数和行驶速度超过90 km/h的频率分别为(　　)‎ A.300　0.25 B.300　0.35‎ C.60　0.25 D.60　0.35‎ 解析由频率分布直方图得,在此路段上汽车行驶速度在区间[85,90)的频率为0.06×5=0.3,∴在此路段上汽车行驶速度在区间[85,90)内的车辆数为0.3×1 000=300.‎ 行驶速度超过90 km/h的频率为(0.05+0.02)×5=0.35.‎ 答案B ‎3.某工厂对一批产品进行了抽样检测,下图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是(　　)‎ A.90 B.75 C.60 D.45‎ 解析设样本容量是n,产品净重小于100克的概率为(0.050+0.100)×2=0.300,已知样本中产品净重小于100克的个数是36,则=0.300,所以n=120.净重大于或等于98克并且小于104克的产品的频率为(0.100+0.150+0.125)×2=0.75.所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.75=90.‎ 答案A ‎4.从某小学随机抽取100名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图).由图中数据可知a=　　　.若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层随机抽样的方法抽取18人参加一项活动,则从身高在[140,150]内的学生中抽取的人数应为　　　　. ‎ 解析所有小矩形的面积和等于10×(0.005+0.010+0.020+a+0.035)=1,解得a=0.030;100名同学中,身高在[120,130)内的学生数是10×0.030×100=30,身高在[130,140)内的学生数是10×0.020×100=20,身高在[140,150]内的学生数是10×0.010×100=10,则三组内的总学生数是30+20+10=60,所以从身高在[140,150]内的学生中选取的人数应为10×=10×=3.‎ 答案0.030　3‎ 素养培优练 ‎　从高一学生中抽取50名参加调研考试,成绩的分组及各组的频数如下(单位:分):‎ ‎[40,50),2;[50,60),3;[60,70),10;[70,80),15;[80,90),12;[90,100],8.‎ ‎(1)列出样本的频率分布表;‎ ‎(2)画出频率分布直方图;‎ ‎(3)估计成绩在[70,80)分的学生所占总体的百分比;‎ ‎(4)估计成绩在[70,100]分的学生所占总体的百分比.‎ 解(1)频率分布表如下:‎ 成绩分组 频数 频率 ‎[40,50)‎ ‎2‎ ‎0.04‎ ‎[50,60)‎ ‎3‎ ‎0.06‎ ‎[60,70)‎ ‎10‎ ‎0.20‎ ‎[70,80)‎ ‎15‎ ‎0.30‎ ‎[80,90)‎ ‎12‎ ‎0.24‎ ‎[90,100]‎ ‎8‎ ‎0.16‎ 合计 ‎50‎ ‎1.00‎ ‎(2)由题意知组距为10,取小矩形的高为,计算得到如下的数据表:‎ 成绩分组 频率 小矩形高 ‎[40,50)‎ ‎0.04‎ ‎0.004‎ ‎[50,60)‎ ‎0.06‎ ‎0.006‎ ‎[60,70)‎ ‎0.2‎ ‎0.02‎ ‎[70,80)‎ ‎0.3‎ ‎0.03‎ ‎[80,90)‎ ‎0.24‎ ‎0.024‎ ‎[90,100]‎ ‎0.16‎ ‎0.016‎ 合计 ‎1.00‎ 根据表格画出如下的频率分布直方图:‎ ‎(3)由频率分布直方图,可估计成绩在[70,80)分的学生所占总体的百分比是0.03×10=0.3=30%.‎ ‎(4)估计成绩在[70,100]分的学生所占总体的百分比是0.3+0.24+0.16=0.7=70%.‎