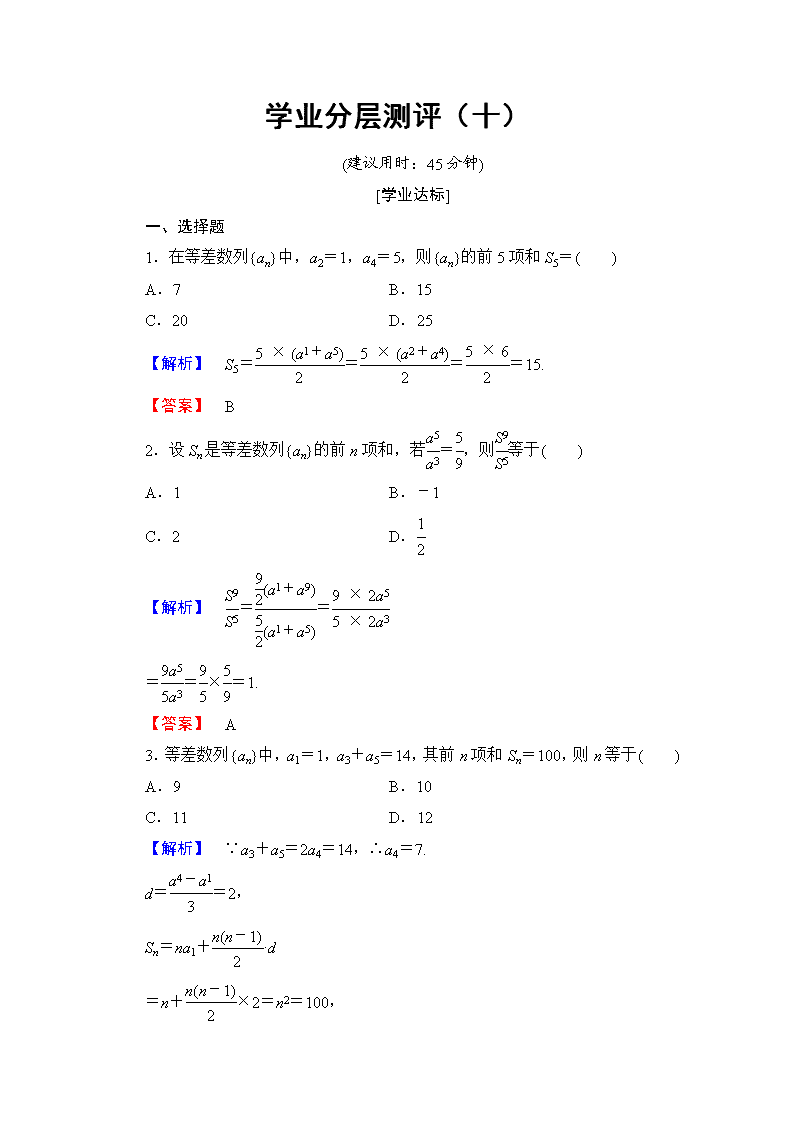高中数学人教a版必修五第二章数列学业分层测评10word版含答案 6页

学业分层测评（十） (建议用时：45 分钟) [学业达标] 一、选择题 1．在等差数列{an}中，a2＝1，a4＝5，则{an}的前 5 项和 S5＝( ) A．7 B．15 C．20 D．25 【解析】 S5＝5×a1＋a5 2 ＝5×a2＋a4 2 ＝5×6 2 ＝15. 【答案】 B 2．设 Sn 是等差数列{an}的前 n 项和，若a5 a3 ＝5 9 ，则S9 S5 等于( ) A．1 B．－1 C．2 D．1 2 【解析】 S9 S5 ＝ 9 2 a1＋a9 5 2 a1＋a5 ＝9×2a5 5×2a3 ＝9a5 5a3 ＝9 5 ×5 9 ＝1. 【答案】 A 3．等差数列{an}中，a1＝1，a3＋a5＝14，其前 n 项和 Sn＝100，则 n 等于( ) A．9 B．10 C．11 D．12 【解析】 ∵a3＋a5＝2a4＝14，∴a4＝7. d＝a4－a1 3 ＝2， Sn＝na1＋nn－1 2 ·d ＝n＋nn－1 2 ×2＝n2＝100， ∴n＝10. 【答案】 B 4．(2015·全国卷Ⅰ)已知{an}是公差为 1 的等差数列，Sn 为{an}的前 n 项和， 若 S8＝4S4，则 a10＝( ) A.17 2 B.19 2 C．10 D．12 【解析】 ∵公差为 1， ∴S8＝8a1＋8×8－1 2 ×1＝8a1＋28，S4＝4a1＋6. ∵S8＝4S4，∴8a1＋28＝4(4a1＋6)，解得 a1＝1 2 ， ∴a10＝a1＋9d＝1 2 ＋9＝19 2 .故选 B. 【答案】 B 5．若数列{an}的通项公式是 an＝(－1)n(3n－2)，则 a1＋a2＋…＋a10＝( ) A．15 B．12 C．－12 D．－15 【解析】 a1＋a2＋…＋a10 ＝－1＋4－7＋10＋…＋(－1)10·(3×10－2) ＝(－1＋4)＋(－7＋10)＋…＋[(－1)9·(3×9－2)＋(－1)10·(3×10－2)] ＝3×5＝15. 【答案】 A 二、填空题 6．已知{an}是等差数列，a4＋a6＝6，其前 5 项和 S5＝10，则其公差为 d ＝ . 【解析】 a4＋a6＝a1＋3d＋a1＋5d＝6，① S5＝5a1＋1 2 ×5×(5－1)d＝10，② 由①②联立解得 a1＝1，d＝1 2. 【答案】 1 2 7．{an}为等差数列，Sn 为其前 n 项和，已知 a7＝5，S7＝21，则 S10＝ . 【解析】 设公差为 d，则由已知得 S7＝7a1＋a7 2 ，即 21＝7a1＋5 2 ，解得 a1 ＝1，所以 a7＝a1＋6d，所以 d＝2 3.所以 S10＝10a1＋10×9 2 d＝10＋10×9 2 ×2 3 ＝40. 【答案】 40 8．若数列 1 nn＋1 的前 n 项和为 Sn，且 Sn＝19 20 ，则 n＝ . 【导学号： 05920068】 【解析】 Sn＝ 1 1×2 ＋ 1 2×3 ＋…＋ 1 nn＋1 ＝1－1 2 ＋1 2 －1 3 ＋1 3 －1 4 ＋…＋1 n － 1 n＋1 ＝1－ 1 n＋1 ＝ n n＋1. 由已知得 n n＋1 ＝19 20 ， 解得 n＝19. 【答案】 19 三、解答题 9．等差数列{an}中，a10＝30，a20＝50. (1)求数列的通项公式； (2)若 Sn＝242，求 n. 【解】 (1)设数列{an}的首项为 a1，公差为 d. 则 a10＝a1＋9d＝30， a20＝a1＋19d＝50， 解得 a1＝12， d＝2， ∴an＝a1＋(n－1)d＝12＋(n－1)×2＝10＋2n. (2)由 Sn＝na1＋nn－1 2 d 以及 a1＝12，d＝2，Sn＝242， 得方程 242＝12n＋nn－1 2 ×2，即 n2＋11n－242＝0，解得 n＝11 或 n＝－22(舍 去)．故 n＝11. 10．在我国古代，9 是数学之极，代表尊贵之意，所以中国古代皇家建筑中包 含许多与9 相关的设计．例如，北京天坛圆丘的地面由扇环形的石板铺成(如图232 所示)，最高一层的中心是一块天心石，围绕它的第 1 圈有 9 块石板，从第 2 圈开 始，每 1 圈比前 1 圈多 9 块，共有 9 圈，则： 图 232 (1)第 9 圈共有多少块石板？ (2)前 9 圈一共有多少块石板？ 【解】 (1)设从第 1 圈到第 9 圈石板数所成数列为{an}，由题意可知{an}是等 差数列，其中 a1＝9，d＝9，n＝9. 由等差数列的通项公式，得第 9 圈石板块数为： a9＝a1＋(9－1)·d＝9＋(9－1)×9＝81(块)． (2)由等差数列前 n 项和公式，得前 9 圈石板总数为： S9＝9a1＋9×9－1 2 d＝9×9＋9×8 2 ×9＝405(块)． 答：第 9 圈共有 81 块石板，前 9 圈一共有 405 块石板． [能力提升] 1．如图 233 所示将若干个点摆成三角形图案，每条边(包括两个端点)有 n(n>1，n∈N*)个点，相应的图案中总的点数记为 an，则 a2＋a3＋a4＋…＋an 等于 ( ) 图 233 A.3n2 2 B.nn＋1 2 C.3nn－1 2 D．nn－1 2 【解析】 由图案的点数可知 a2＝3，a3＝6，a4＝9，a5＝12，所以 an＝3n－3， n≥2， 所以 a2＋a3＋a4＋…＋an＝n－13＋3n－3 2 ＝3nn－1 2 . 【答案】 C 2．已知命题：“在等差数列{an}中，若 4a2＋a10＋a( )＝24，则 S11 为定值” 为真命题，由于印刷问题，括号处的数模糊不清，可推得括号内的数为( ) A．15 B．24 C．18 D．28 【解析】 设括号内的数为 n，则 4a2＋a10＋a(n)＝24， ∴6a1＋(n＋12)d＝24. 又 S11＝11a1＋55d＝11(a1＋5d)为定值， 所以 a1＋5d 为定值． 所以n＋12 6 ＝5，n＝18. 【答案】 C 3．(2015·安徽高考)已知数列{an}中，a1＝1，an＝an－1＋1 2(n≥2)，则数列{an} 的前 9 项和等于 ． 【解析】 由 a1＝1，an＝an－1＋1 2(n≥2)，可知数列{an}是首项为 1，公差为1 2 的 等差数列，故 S9＝9a1＋9×9－1 2 ×1 2 ＝9＋18＝27. 【答案】 27 4．(2015·全国卷Ⅰ)Sn 为数列{an}的前 n 项和．已知 an＞0，a2n＋2an＝4Sn＋3. (1)求{an}的通项公式； (2)设 bn＝ 1 anan＋1 ，求数列{bn}的前 n 项和． 【解】 (1)由 a2n＋2an＝4Sn＋3， ① 可知 a2n＋1＋2an＋1＝4Sn＋1＋3. ② ②－①，得 a2n＋1－a2n＋2(an＋1－an)＝4an＋1， 即 2(an＋1＋an)＝a2n＋1－a2n＝(an＋1＋an)(an＋1－an)． 由 an>0，得 an＋1－an＝2. 又 a21＋2a1＝4a1＋3，解得 a1＝－1(舍去)或 a1＝3. 所以{an}是首项为 3，公差为 2 的等差数列，通项公式为 an＝2n＋1. (2)由 an＝2n＋1 可知 bn＝ 1 anan＋1 ＝ 1 2n＋12n＋3 ＝1 2 1 2n＋1 － 1 2n＋3 . 设数列{bn}的前 n 项和为 Tn，则 Tn＝b1＋b2＋…＋bn＝ 1 2 1 3 －1 5 ＋ 1 5 －1 7 ＋…＋ 1 2n＋1 － 1 2n＋3 ＝ n 32n＋3.