2020-2021学年北师大版数学必修2习题：第一章 立体几何初步 阶段性评估1 11页

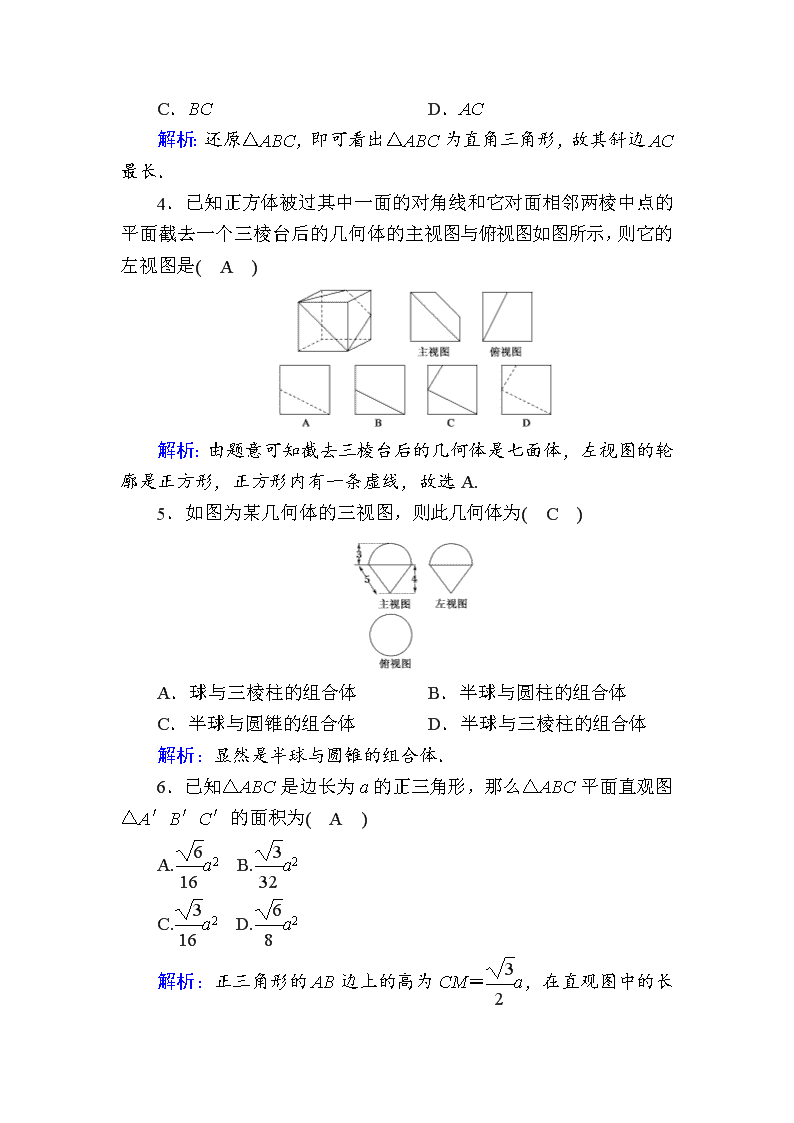
阶段性评估(一) 第Ⅰ卷(选择题 共 60 分) 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分，在每小 题给出的四个选项中，只有一项是符合要求的) 1．下列平面图形中，能够旋转得到左图的是( A ) 解析：由四个选项中的平面图形旋转后与原图比较知 A 正确． 2．下列说法错误的是( D ) A．多面体至少有四个面 B．长方体、正方体都是棱柱 C．九棱柱有 9 条侧棱、9 个侧面，侧面均为平行四边形 D．三棱柱的侧面为三角形 解析：对于 A，面最少的多面体是三棱锥，故多面体至少有四个 面，故 A 正确；对于 B，长方体和正方体都是四棱柱，故 B 正确； 对于 C，由棱柱的定义知九棱柱有 9 条侧棱、9 个侧面，侧面均为平 行四边形，故 C 正确；对于 D，三棱柱的侧面为平行四边形，故 D 错误． 3．如图所示，△A′B′C′是水平放置的△ABC 的直观图，则 在原△ABC 的三边及中线 AD 中，最长的线段是( D ) A．AB B．AD C．BC D．AC 解析：还原△ABC，即可看出△ABC 为直角三角形，故其斜边 AC 最长． 4．已知正方体被过其中一面的对角线和它对面相邻两棱中点的 平面截去一个三棱台后的几何体的主视图与俯视图如图所示，则它的 左视图是( A ) 解析：由题意可知截去三棱台后的几何体是七面体，左视图的轮 廓是正方形，正方形内有一条虚线，故选 A. 5．如图为某几何体的三视图，则此几何体为( C ) A．球与三棱柱的组合体 B．半球与圆柱的组合体 C．半球与圆锥的组合体 D．半球与三棱柱的组合体 解析：显然是半球与圆锥的组合体． 6．已知△ABC 是边长为 a 的正三角形，那么△ABC 平面直观图 △A′B′C′的面积为( A ) A. 6 16a2 B. 3 32a2 C. 3 16a2 D. 6 8 a2 解析：正三角形的 AB 边上的高为 CM＝ 3 2 a，在直观图中的长度 为 C′M′＝ 3 4 a，故△A′B′C′的面积为1 2·a· 3 4 a· 2 2 ＝ 6 16a2. 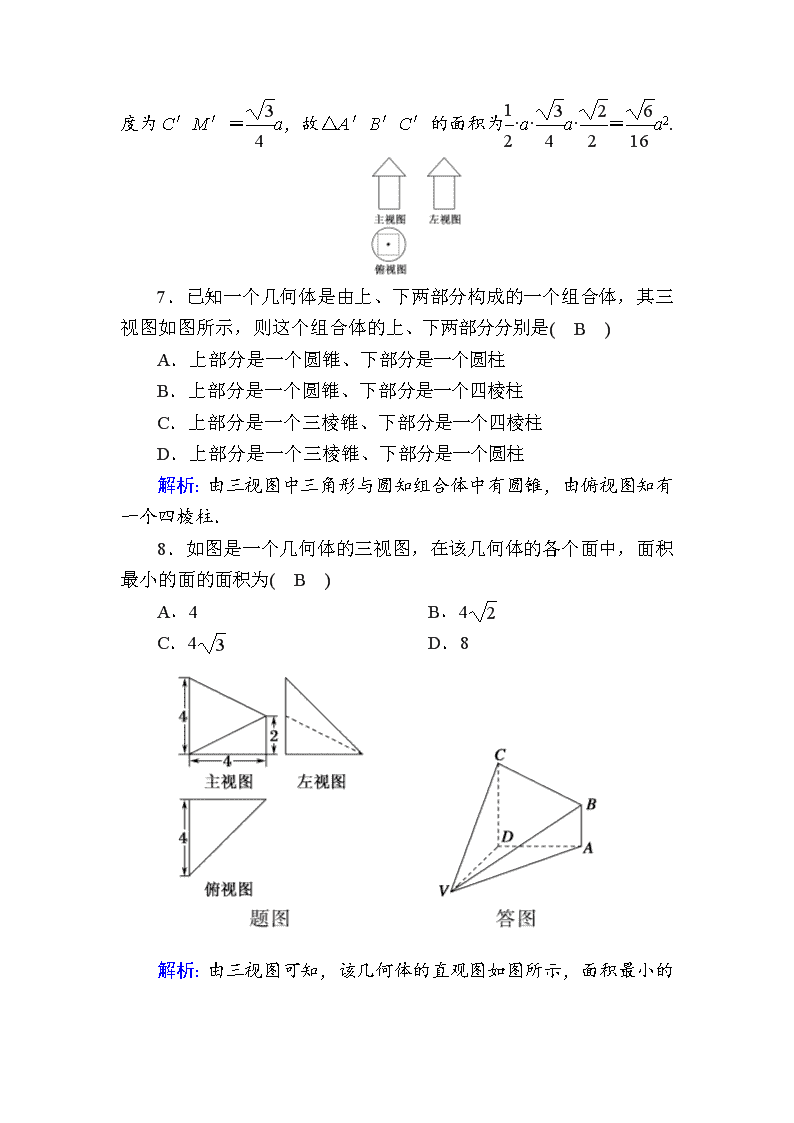7．已知一个几何体是由上、下两部分构成的一个组合体，其三 视图如图所示，则这个组合体的上、下两部分分别是( B ) A．上部分是一个圆锥、下部分是一个圆柱 B．上部分是一个圆锥、下部分是一个四棱柱 C．上部分是一个三棱锥、下部分是一个四棱柱 D．上部分是一个三棱锥、下部分是一个圆柱 解析：由三视图中三角形与圆知组合体中有圆锥，由俯视图知有 一个四棱柱． 8．如图是一个几何体的三视图，在该几何体的各个面中，面积 最小的面的面积为( B ) A．4 B．4 2 C．4 3 D．8 解析：由三视图可知，该几何体的直观图如图所示，面积最小的 面为面 VAB，其面积 S＝1 2 ×2×4 2＝4 2.故选 B. 9．直角边分别为 1 和 3的三角形，绕一条直角边所在直线旋转， 形成的圆锥的俯视图是半径为 1 的圆，则它的主视图是( C ) A．等腰直角三角形 B．边长为 3的等边三角形 C．边长为 2 的等边三角形 D．不能确定 解析：由俯视图知长为 3的边在轴上．因此主视图为边长为 2 的等边三角形． 10．底面水平放置的正三棱柱的所有棱长均为 2，当其主视图有 最大面积时，其左视图的面积为( A ) A．2 3 B．3 C. 3 D．4 解析：当主视图的面积最大时，可知其正三棱柱某个侧面的面积， 可以按如图所示放置，此时 S 左＝2 3. 11．一四面体的三视图如图所示，则该四面体四个面中最大的面 积是( D ) A．2 B．2 2 C. 3 D．2 3 解析：由四面体的三视图知其直观图为如图所示的正方体中的四 面体 A－BCD，由三视图知正方体的棱长为 2. 所以 S△ABD＝1 2 ×2×2 2＝2 2， S△ADC＝1 2 ×2 2×2 2× 3 2 ＝2 3， S△ABC＝1 2 ×2×2 2＝2 2， S△BCD＝1 2 ×2×2＝2. 所以所求的最大面积为 2 3.故选 D. 12．如图所示，在透明塑料制成的长方体容器内灌进一些水，将 容器倾斜，随着倾斜程度的不同，则有下列说法： ①水的形状成棱柱形(如图 1)； ②水的形状成棱台形(如图 2)； ③水的形状成棱锥形(如图 3)． 其中正确的说法是( A ) A．① B．①② C．②③ D．①②③ 解析：①正确；②③中水的形状是棱柱形．故选 A. 第Ⅱ卷(非选择题 共 90 分) 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分，请把答案 填写在题中横线上) 13．一个棱柱至少有 5 个面，面数最少的棱锥有 4 个顶点，顶点 最少的棱台有 3 条侧棱． 解析：由棱柱、棱锥、棱台的定义可得． 14．如图所示，在正方体 ABCD－A1B1C1D1 中，M，N 分别是 BB1， BC 的中点，则图中阴影部分在平面 ADD1A1 上的投影为图中的①. 解析：点 M，N 在平面 ADD1A1 上的正投影分别是 AA1，AD 的中 点，由此可得三角形 MND 在平面 ADD1A1 上的投影． 15．已知正三棱锥 V—ABC 的主视图、俯视图如图所示，其中 VA＝4，AC＝2 3，则该三棱锥的左视图的面积为 6. 解析：此正三棱锥的侧棱长是 4，底面正三角形的边长是 2 3， 而其左视图是等腰三角形，底边长是 2 3，高是三棱锥的高，即为 2 3， 所以左视图的面积是 6. 16．一块石材表示的几何体的三视图如图所示，将该石材切削、 打磨，加工成球，则能得到的最大球的半径等于 2. 解析：由三视图可知，这是一个三棱柱，内切球在主视图中的投 影是主视图的内切圆，设其半径为 r，根据三角形面积公式有1 2(6＋8 ＋10)r＝1 2 ×6×8，解得 r＝2. 三、解答题(本大题共 6 小题，共 70 分．解答应写出文字说明， 证明过程或演算步骤) 17．(10 分)如图所示的几何体的侧面展开图是一个矩形，且几何 体的底面边长均为 3，侧面的棱长为 5，已知点 P 是棱 AA1 上一动点， Q 是棱 BB1 上一动点，求 CP＋PQ＋QC1 的最小值． 解：将几何体沿棱 CC1 剪开，其侧面展开为平面图形，如图所示， CP＋PQ＋QC1 的最小值即平面图中矩形对角线 CC1 的长，所以(CP ＋PQ＋QC1)min＝ 3＋3＋32＋52＝ 106. 18．(12 分)如图所示，四边形 ABCD 是一个梯形，CD∥AB，CD ＝BO＝1，三角形 AOD 为等腰直角三角形，O 为 AB 的中点，试求梯 形 ABCD 水平放置的直观图的面积． 解：法一：在梯形 ABCD 中，AB＝2，高 OD＝1，由于梯形 ABCD 水平放置的直观图仍为梯形，且上底 CD 和下底 AB 的长度都不变， 如图所示，在直观图中， O′D′ ＝ 1 2 OD ＝ 1 2 ， 梯 形 的 高 D′E′ ＝ 2 4 ， 于 是 梯 形 A′B′C′D′的面积为1 2 ×(1＋2)× 2 4 ＝3 2 8 . 法二：梯形 ABCD 的面积 S＝1 2(DC＋AB)×OD＝1 2(1＋2)×1＝3 2. 所以梯形 ABCD 直观图的面积为 S′＝ 2 4 S＝ 2 4 ×3 2 ＝3 2 8 . 19．(12 分)如图所示是一个半圆柱 OO1 与三棱柱 ABC—A1B1C1 的组合体，其中，圆柱 OO1 的轴截面 ACC1A1 是边长为 4 的正方形， △ABC 为等腰直角三角形，AB⊥BC，试画出此组合体的三视图． 解：由题意可知几何体的主视图与左视图都是中间有一条线段的 矩形，俯视图由半圆与等腰直角三角形组成，如图： 20．(12 分)根据所给三视图，画出物体的直观图． 解：(1)画轴．建立空间直角坐标系，使∠xOy＝45°，∠xOz＝90°， 如图①. (2)画圆柱的两底面和圆台的上底面．画出底面圆 O，在 z 轴上截 取点 O′，使 OO′等于三视图中相应高度．过 O′作 Ox 的平行线 O′x′，Oy 的平行线 O′y′，利用 O′x′与 O′y′画出底面圆 O′(与画圆 O 一样)．再在 z 轴上截取点 O″，使 O′O″等于三视图 中相应高度．过 O″作 Ox 的平行线 O″x″，Oy 的平行线 O″y″， 利用 O″x″与 O″y″画出底面圆 O″. (3)成图．连接 AA′，A′A″，B″B′，B′B，整理得到三视 图所表示的立体图形的直观图，如图②. 21 ． (12 分 ) 已 知 圆 锥 的 底 面 半 径 为 r ， 高 为 h ， 正 方 体 ABCD—A1B1C1D1 内接于圆锥，求这个正方体的棱长． 解： 过内接正方体的一组对棱作圆锥的轴截面，如图所示，设圆锥内 接正方体的棱长为 x，则在轴截面中，正方体的对角面 A1ACC1 的一 组邻边的长分别为 x 和 2x. ∵△VA1C1∽△VMN，∴ 2x 2r ＝h－x h . ∴ 2hx＝2rh－2rx，∴x＝ 2rh 2r＋ 2h. 即圆锥内接正方体的棱长为 2rh 2r＋ 2h. 22．(12 分)圆台的上、下底面半径分别为 5 cm,10 cm，母线长 AB＝20 cm，从圆台母线 AB 的中点 M 拉一条绳子绕圆台侧面转到点 A，求： (1)绳子的最短长度； (2)在绳子最短时，上底圆周上的点到绳子的最短距离． 解： (1)如右图所示，将侧面展开，绳子的最短距离为侧面展开图中 AM 的长度，θ＝10－5 20 ×360°＝90°. 设 OB′＝L′，则 5 L′·360°＝90°，L′＝20 cm. ∴OA＝40 cm，OM＝30 cm. ∴AM＝ OA2＋OM2＝50 cm. 即绳子最短长度为 50 cm. (2)作 OQ⊥AM 于点 Q，交弧 BB′于点 P， 则 PQ 为所求的最短距离． ∵OA·OM＝AM·OQ.∴OQ＝24 cm. 故 PQ＝OQ－OP＝24－20＝4 (cm)，即上底圆周上的点到绳子的 最短距离为 4 cm.