2020高中数学奇偶性的应用 5页

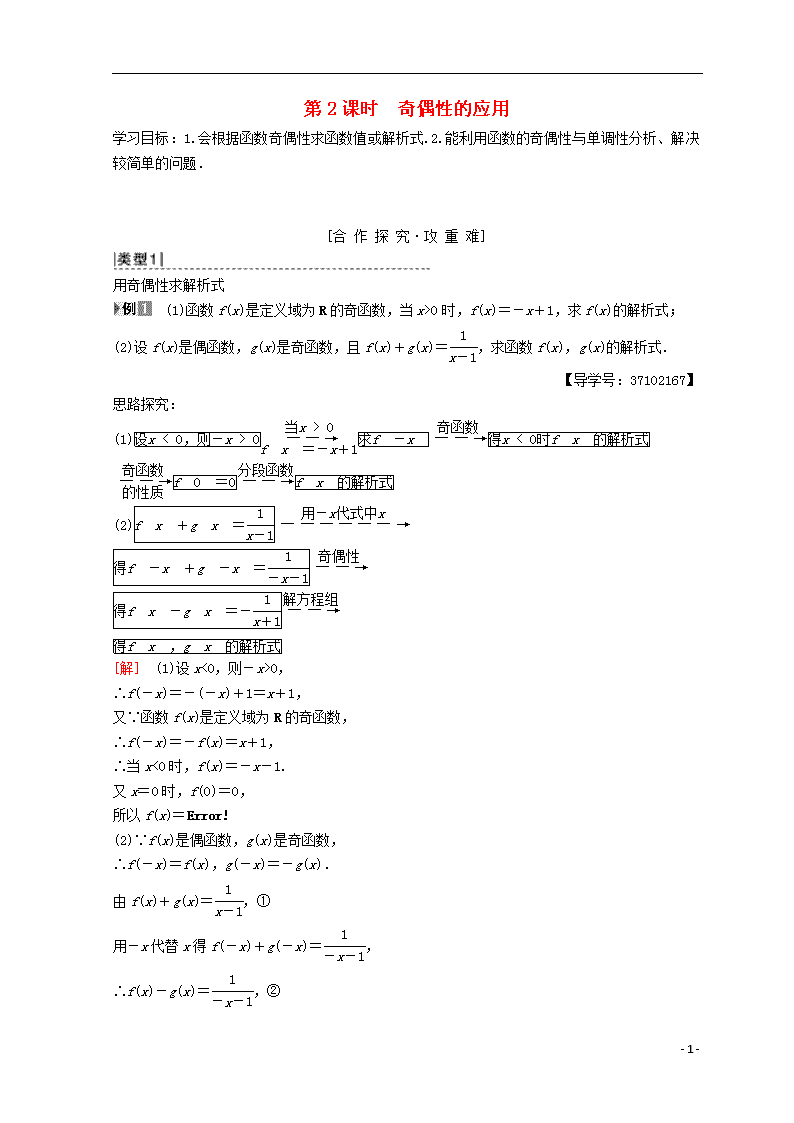
第2课时　奇偶性的应用 学习目标：1.会根据函数奇偶性求函数值或解析式.2.能利用函数的奇偶性与单调性分析、解决较简单的问题．‎ ‎[合 作 探 究·攻 重 难]‎ 用奇偶性求解析式 ‎　(1)函数f(x)是定义域为R的奇函数，当x>0时，f(x)＝－x＋1，求f(x)的解析式；‎ ‎(2)设f(x)是偶函数，g(x)是奇函数，且f(x)＋g(x)＝，求函数f(x)，g(x)的解析式. ‎ ‎【导学号：37102167】‎ 思路探究：(1) ‎(2) ‎[解]　(1)设x<0，则－x>0，‎ ‎∴f(－x)＝－(－x)＋1＝x＋1，‎ 又∵函数f(x)是定义域为R的奇函数，‎ ‎∴f(－x)＝－f(x)＝x＋1，‎ ‎∴当x<0时，f(x)＝－x－1.‎ 又x＝0时，f(0)＝0，‎ 所以f(x)＝ ‎(2)∵f(x)是偶函数，g(x)是奇函数，‎ ‎∴f(－x)＝f(x)，g(－x)＝－g(x)．‎ 由f(x)＋g(x)＝，①‎ 用－x代替x得f(－x)＋g(－x)＝，‎ ‎∴f(x)－g(x)＝，②‎ ‎(①＋②)÷2，得f(x)＝；‎ - 5 -‎ ‎(①－②)÷2，得g(x)＝.‎ 母题探究：1.把本例(1)的条件“奇函数”改为“偶函数”，当“x>0”改为“x≥0”，再求f(x)的解析式．‎ ‎[解]　设x≤0，则－x≥0，则f(－x)＝x＋1.‎ 又f(－x)＝f(x)，所以f(x)＝x＋1.‎ 故f(x)的解析式为f(x)＝ ‎2．把本例(2)的条件“f(x)是偶函数，g(x)是奇函数”改为“f(x)是奇函数，g(x)是偶函数”，再求f(x)，g(x)的解析式．‎ ‎[解]　∵f(x)是奇函数，g(x)是偶函数，‎ ‎∴f(－x)＝－f(x)，g(－x)＝g(x)，‎ 又f(x)＋g(x)＝，①‎ 用－x代替上式中的x，得 f(－x)＋g(－x)＝，‎ 即f(x)－g(x)＝.②‎ 联立①②得 f(x)＝，g(x)＝.‎ ‎[规律方法]　利用函数奇偶性求解析式的方法 (1)“求谁设谁”，既在哪个区间上求解析式，x就应在哪个区间上设.‎ (2)要利用已知区间的解析式进行代入.‎ (3)利用f(x)的奇偶性写出－f(x)或f(－x)，从而解出f(x).‎ 提醒：若函数f(x)的定义域内含0且为奇函数，则必有f(0)＝0，但若为偶函数，未必有f(0)＝0.‎ 函数单调性和奇偶性的综合问题 ‎[探究问题]‎ ‎1．如果奇函数f(x)在区间(a，b)上单调递增，那么f(x)在(－b，－a)上的单调性如何？‎ 如果偶函数f(x)在区间(a，b)上单调递减，那么f(x)在(－b，－a)上的单调性如何？‎ 提示：如果奇函数f(x)在区间(a，b)上单调递增，那么f(x)在(－b，－a)上单调递增；如果偶函数f(x)在区间(a，b)上单调递减，那么f(x)在(－b，－a)上单调递增．‎ ‎2．你能否把上述问题所得出的结论用一句话概括出来？‎ 提示：‎ - 5 -‎ 奇函数在关于原点对称的区间上单调性相同，偶函数在关于原点对称的区间上单调性相反．‎ ‎3．若偶函数f(x)在(－∞，0)上单调递增，那么f(3)和f(－2)的大小关系如何？若f(a)>f(b)，你能得到什么结论？‎ 提示：f(－2)>f(3)，若f(a)>f(b)，则|a|<|b|.‎ 角度一　比较大小问题 ‎　函数y＝f(x)在[0,2]上单调递增，且函数f(x＋2)是偶函数，则下列结论成立的是(　　)‎ ‎【导学号：37102168】‎ A．f(1)0，则x - 5 -‎ 的取值范围是________．‎ ‎(－1,3)　[∵f(2)＝0，f(x－1)>0，∴f(x－1)>f(2)，‎ 又∵f(x)是偶函数，且在[0，＋∞)上单调递减，‎ ‎∴f(|x－1|)>f(2)，∴|x－1|<2，∴－2f(x2)或f(x1)f(2)转化得f(|x－1|)>f(2)，再由f(x)在[0，＋∞)上单调递减即可脱去“f”，得到|x－1|<2.其优点在于避免了讨论.‎ ‎[跟踪训练]‎ ‎2．函数f(x)是定义在实数集上的偶函数，且在[0，＋∞)上是增函数，f(3)1　　　　　　　 B．a<－2‎ C．a>1或a<－2 D．－11或a<－2.故选C.]‎ ‎[当 堂 达 标·固 双 基]‎ ‎1．已知函数y＝f(x)为奇函数，且当x>0时，f(x)＝x2－2x＋3，则当x<0时，f(x)的解析式是(　　)‎ A．f(x)＝－x2＋2x－3 B．f(x)＝－x2－2x－3‎ C．f(x)＝x2－2x＋3 D．f(x)＝－x2－2x＋3‎ B　[若x<0，则－x>0，因为当x>0时，f(x)＝x2－2x＋3，所以f(－x)＝x2＋2x＋3，因为函数f(x)是奇函数，所以f(－x)＝x2＋2x＋3＝－f(x)，所以f(x)＝－x2－2x－3，所以x<0时，f(x)＝－x2－2x－3.故选B.]‎ ‎2．已知偶函数在(－∞，0)上单调递增，则(　　)‎ ‎【导学号：37102170】‎ A．f(1)>f(2) B．f(1)f(2)，故选A.]‎ ‎3．定义在R上的偶函数f(x)在[0，＋∞)上是增函数，若f(a)b - 5 -‎ C．|a|<|b| D．0≤ab≥0‎ C　[∵f(x)是R上的偶函数，且在[0，＋∞)上是增函数，‎ ‎∴由f(a)