浙江专用2020高考数学二轮复习专题二三角函数平面向量与复数高考解答题的审题与答题示范二教案 2页

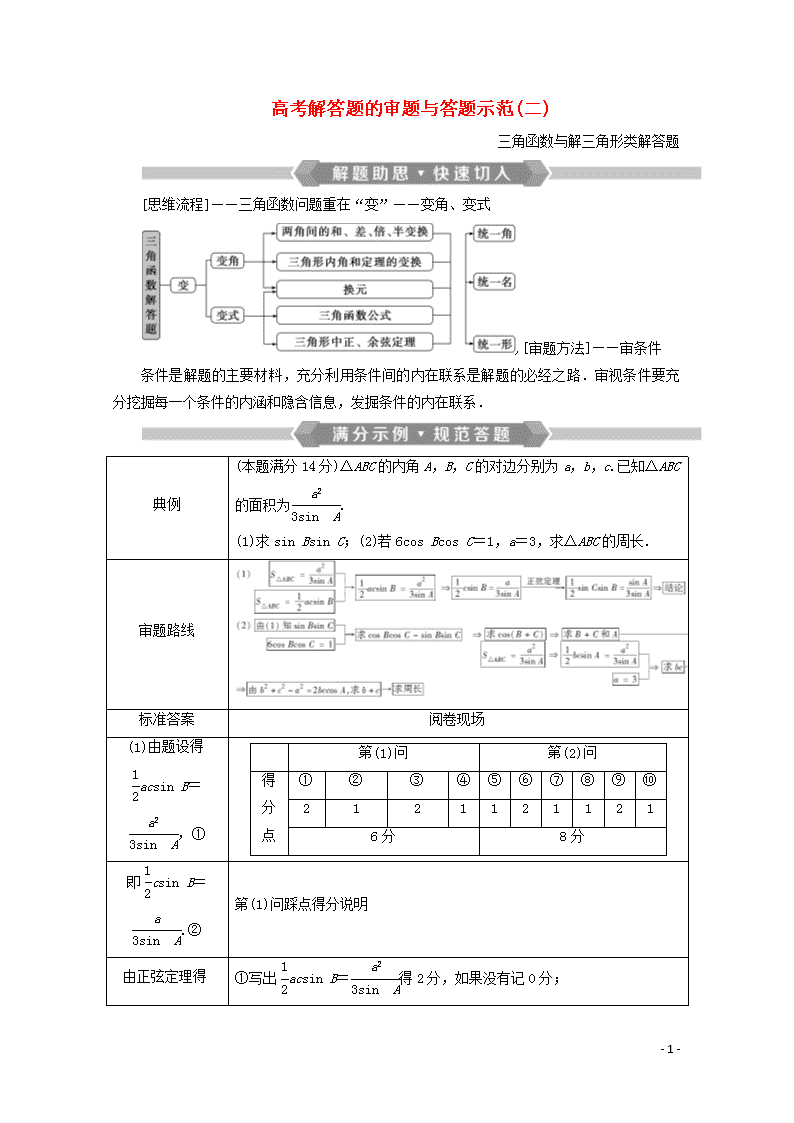
- 1 - 高考解答题的审题与答题示范(二) 三角函数与解三角形类解答题 [思维流程]——三角函数问题重在“变”——变角、变式 ,[审题方法]——审条件 条件是解题的主要材料，充分利用条件间的内在联系是解题的必经之路．审视条件要充 分挖掘每一个条件的内涵和隐含信息，发掘条件的内在联系． 典例 (本题满分 14 分)△ABC 的内角 A，B，C 的对边分别为 a，b，c.已知△ABC 的面积为 a2 3sin A . (1)求 sin Bsin C；(2)若 6cos Bcos C＝1，a＝3，求△ABC 的周长. 审题路线 标准答案 阅卷现场 (1)由题设得 1 2 acsin B＝ a2 3sin A ，① 第(1)问 第(2)问 得 分 点 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ 2 1 2 1 1 2 1 1 2 1 6 分 8 分 即 1 2 csin B＝ a 3sin A .② 第(1)问踩点得分说明 由正弦定理得 ①写出 1 2 acsin B＝ a2 3sin A 得 2 分，如果没有记 0 分； - 2 - 1 2 sin Csin B＝ sin A 3sin A 变式．③ 故 sin Bsin C＝ 2 3 .④ ②正确变形，得出 1 2 csin B＝ a 3sin A 得 1 分，越过此步不扣分； (2)由题设及(1) ③正确写出 1 2 sin Csin B＝ sin A 3sin A 得 2 分； 得 cos Bcos C－ sin Bsin C＝－1 2 ， ⑤ ④正确叙述结论得 1 分. 即 cos(B＋C)＝－ 1 2 ，所以 B＋C＝ 2π 3 ，故 A＝π 3 .⑥ 第(2)问踩点得分说明 由题设得 1 2 bcsin A＝ a2 3sin A ，⑦ ⑤写出 cos Bcos C－sin Bsin C＝－1 2 得 1 分； 即 bc＝8.⑧ ⑥正确求出 A 得 2 分； 由余弦定理得 b2 ＋c2－bc＝9， ⑦正确写出 1 2 bcsin A＝ a2 3sin A 得 1 分； 即(b＋c)2－3bc ＝9，得 b＋c＝ 33.⑨ ⑧求出 bc 的值，正确得 1 分，错误不得分； 故△ABC 的周长为 3＋ 33.⑩ ⑨通过变形得出 b＋c＝ 33得 2 分； ⑩正确写出答案得 1 分.