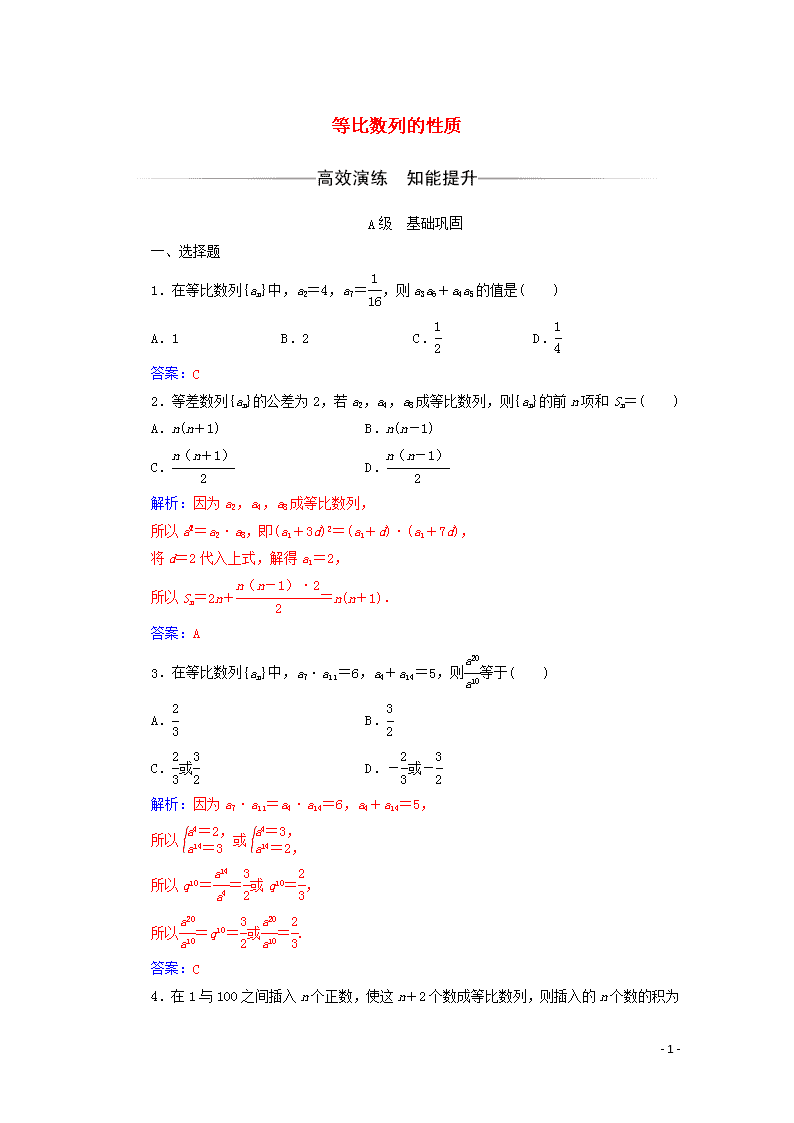高中数学第二章数列2-4等比数列第2课时等比数列的性质达标检测含解析新人教A版必修5 5页

等比数列的性质 A级　基础巩固 一、选择题 ‎1．在等比数列{an}中，a2＝4，a7＝，则a3a6＋a4a5的值是(　　)‎ A．1 B．2 C． D． 答案：C ‎2．等差数列{an}的公差为2，若a2，a4，a8成等比数列，则{an}的前n项和Sn＝(　　)‎ A．n(n＋1) B．n(n－1)‎ C． D． 解析：因为a2，a4，a8成等比数列，‎ 所以a＝a2·a8，即(a1＋3d)2＝(a1＋d)·(a1＋7d)，‎ 将d＝2代入上式，解得a1＝2，‎ 所以Sn＝2n＋＝n(n＋1)．‎ 答案：A ‎3．在等比数列{an}中，a7·a11＝6，a4＋a14＝5，则等于(　　)‎ A． B． C．或 D．－或－ 解析：因为a7·a11＝a4·a14＝6，a4＋a14＝5，‎ 所以或 所以q10＝＝或q10＝，‎ 所以＝q10＝或＝.‎ 答案：C ‎4．在1与100之间插入n个正数，使这n＋2个数成等比数列，则插入的n个数的积为(　　)‎ A．10n B．n10 C．100n D．n100‎ - 5 -‎ 解析：设这n＋2个数为a1，a2，…，an＋1，an＋2，‎ 则a2·a3·…·an＋1＝(a1an＋2)＝(100)＝10n.‎ 答案：A ‎5．等比数列{an}中，an∈R＋，a4·a5＝32，则log2a1＋log2a2＋…＋log2a8的值为(　　)‎ A．10 B．20 C．36 D．128‎ 解析：log2a1＋log2a2＋…＋log2a8‎ ‎＝log2(a1·a2·a3·…·a8)‎ ‎＝log2(a4a5)4‎ ‎＝4log232‎ ‎＝20.‎ 答案：B 二、填空题 ‎6．等比数列{an}中，a1＜0，{an}是递增数列，则满足条件的q的取值范围是______________．‎ 解析：由an＋1＞an⇒a1qn＞a1qn－1，‎ 因为a1＜0，‎ 所以qn＜qn－1⇒qn＜0对任意正整数n都成立．‎ 所以q＞0且1－＜0解得：0＜q＜1.‎ 答案：0＜q＜1‎ ‎7．已知在公比为q的等比数列{an}中，a5＋a9＝q，则a6(a2＋2a6＋a10)的值为________．‎ 解析：因为a5＋a9＝q，‎ 所以a4＋a8＝，‎ 所以a6(a2＋2a6＋a10)＝a6a2＋2a＋a6a10＝a＋2a4a8＋a＝(a4＋a8)2＝.‎ 答案： ‎8．已知在等比数列{an}中，a3a11＝4a7，数列{bn}是等差数列，且a7＝b7，则b5＋b9＝________．‎ 解析：a3a11＝4a7＝a，‎ - 5 -‎ 所以a7＝4(a7＝0舍去)，‎ 因为{bn}是等差数列，‎ 所以b7＝(b5＋b9)，‎ 又b7＝a7，所以b5＋b9＝8.‎ 答案：8‎ 三、解答题 ‎9．在正项等比数列{an}中，a1a5－2a3a5＋a3a7＝36，a2a4＋2a2a6＋a4a6＝100，求数列{an}的通项公式．‎ 解：因为a1a5＝a，a3a7＝a，‎ 所以由题意，得a－2a3a5＋a＝36，‎ 同理得a＋2a3a5＋a＝100，‎ 所以 因为an>0，所以 解得或 分别解得或 所以an＝a1qn－1＝2n－2或an＝a1qn－1＝26－n.‎ ‎10．三个正数成等比数列，它们的和等于21，倒数的和等于，求这三个数．‎ 解：设三个数为，a，aq(a，q>0)，‎ 由题 所以⇒a2＝21×＝36，‎ 所以a＝6，q＝2或，‎ 所以三个数为3，6，12或12，6，3.‎ B级　能力提升 ‎1．等比数列x，3x＋3，6x＋6，…的第四项等于(　　)‎ - 5 -‎ A．－24 B．0 C．12 D．24‎ 解析：由题意知(3x＋3)2＝x(6x＋6)，即x2＋4x＋3＝0，解得x＝－3或x＝－1(舍去)，所以等比数列的前3项是－3，－6，－12，则第四项为－24.‎ 答案：A ‎2．数列{an}是等差数列，若a1＋1，a3＋3，a5＋5构成公比为q的等比数列，则q＝________．‎ 解析：设{an}的公差为d，则a3＋3＝a1＋1＋2d＋2，a5＋5＝‎ a1＋1＋4d＋4，由题意可得(a3＋3)2＝(a1＋1)(a5＋5)．‎ 所以[(a1＋1)＋2(d＋1)]2＝(a1＋1)[(a1＋1)＋4(d＋1)]，‎ 所以(a1＋1)2＋4(d＋1)(a1＋1)＋[2(d＋1)]2＝(a1＋1)2＋4(a1＋1)(d＋1)，‎ 所以d＝－1，所以a3＋3＝a1＋1，‎ 所以公比q＝＝1.‎ 答案：1‎ ‎3．容器A中盛有浓度为a%的农药mL，容器B中盛有浓度为b%的同种农药mL，A，B两容器中农药的浓度差为20%(a＞b)，先将A中农药的倒入B中，混合均匀后，再由B倒入一部分到A中，恰好使A中保持mL，问至少经过多少次这样的操作，两容器中农药的浓度差小于1%?‎ 解：设第n次操作后，A中农药的浓度为an，B中农药的浓度为bn，则a0＝a%，b0＝b%.‎ b1＝(a0＋4b0)，a1＝a0＋b1＝(4a0＋b0)；‎ b2＝(a1＋4b1)，a2＝a1＋b2＝(4a1＋b1)；‎ ‎…‎ bn＝(an－1＋4bn－1)．‎ an＝(4an－1＋bn－1)，‎ 所以an－bn＝(an－1－bn－1)＝(a0－b0)·.‎ 因为a0－b0＝，‎ 所以an－bn＝·.‎ 依题意知·＜1%，n∈N*，‎ 解得n≥6.‎ - 5 -‎ 故至少经过6次这样的操作，两容器中农药的浓度差小于1%.‎ - 5 -‎