福建省泉州市2020届普通高中毕业班第一次质量检查 文科数学（PDF版） 16页

市质检数学（文科）试题 第 1 页（共 6 页） 准考证号________________ 姓名________________ （在此卷上答题无效） 保密★启用前 泉州市 2020 届普通高中毕业班第一次质量检查 文 科 数 学 本试卷共 23 题，满分 150 分，共 5 页．考试时间 120 分钟． 注意事项： 1．答题前，考生先将自己的姓名、准考证号填写在答题卡上。 2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域（黑色线框）内作答， 超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效。 3．选择题答案使用 2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选 择题答案使用 5.0 毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。 4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分．在每小题给出的四个选项中，只有一项是符合题 目要求的． 1．已知集合  1,0,1,2M   ，  ( 2)( 1) 0N x x x   Z ≤ ，则 M N  A． 1,0,1 B． 0,1,2 C． 1 0,1,2 ， D． 2, 1,0,1 2  ， 2．若 ix y ( ,x y R )与 3 i 1 i   互为共轭复数，则 x y  A．0 B．3 C． 1 D．4 3．记 nS 为等差数列{ }na 的前 n 项和．若 2 5a   ， 4 16S   ，则 6a  A．5 B． 3 C． 12 D． 13 4．已知角 的顶点与坐标原点重合，始边与 x 轴的非负半轴重合，若点 (2, 1)P  在角 的终边上，则 )22sin(   = A． 4 5  B． 4 5 C． 5 3 D． 5 3 市质检数学（文科）试题 第 2 页（共 6 页） 5．执行如图所示的程序框图，若输入 2020m = ， 520n = ，则输出的i = A． 4 B．5 C． 6 D． 7 6．已知椭圆 2 2 2 2: 1( 0)x yE a ba b     的左、右焦点分别为 1F ， 2F ，过 2F 的直线 2 4 0x y   与 y 轴交于点 A ，线段 2AF 与 E 交于点 B . 若 1| | | |AB BF ，则 E 的方程为 A． 2 2 140 36 x y  B． 2 2 120 16 x y  C． 2 2 110 6 x y  D． 2 2 15 x y  7．已知函数 e 1( ) e 1 x xf x   ， )2( 3.0fa  ， )2.0( 3.0fb  ， )2(log 3.0fc  ， 则 cba ,, 的大小关系为 A． cab  B． abc  C． acb  D． bac  8. ABC△ 中， =2 5BC ， D 为 BC 的中点， π 4BAD ∠ ， 1AD  ，则 AC  A． 2 5 B． 2 2 C．6 5 D． 2 9．若 [0,1]x 时， e 2 0x x a  ≥ ，则 a 的取值范围为 A． ]1,1[ B． ]2e,e2[  C． ]1,e2[  D． ]1,22ln2[  10．若双曲线 2 2 : 1( 0)x yE mnm n    绕其对称中心旋转 π 3 后可得某一函数的图象，则 E 的离心率等于 A． 2 3 3 B． 3 C． 2 或 2 3 3 D． 2 或 3 市质检数学（文科）试题 第 3 页（共 6 页） 二、多项选择题：本题共 2 小题，每小题 5 分，共 10 分。在每小题给出的四个选项中，有多项符合题目 要求. 不选或选出的选项中含有错误选项得 0 分，只选出部分正确选项得 3 分，选出全部正确选项得 5 分. 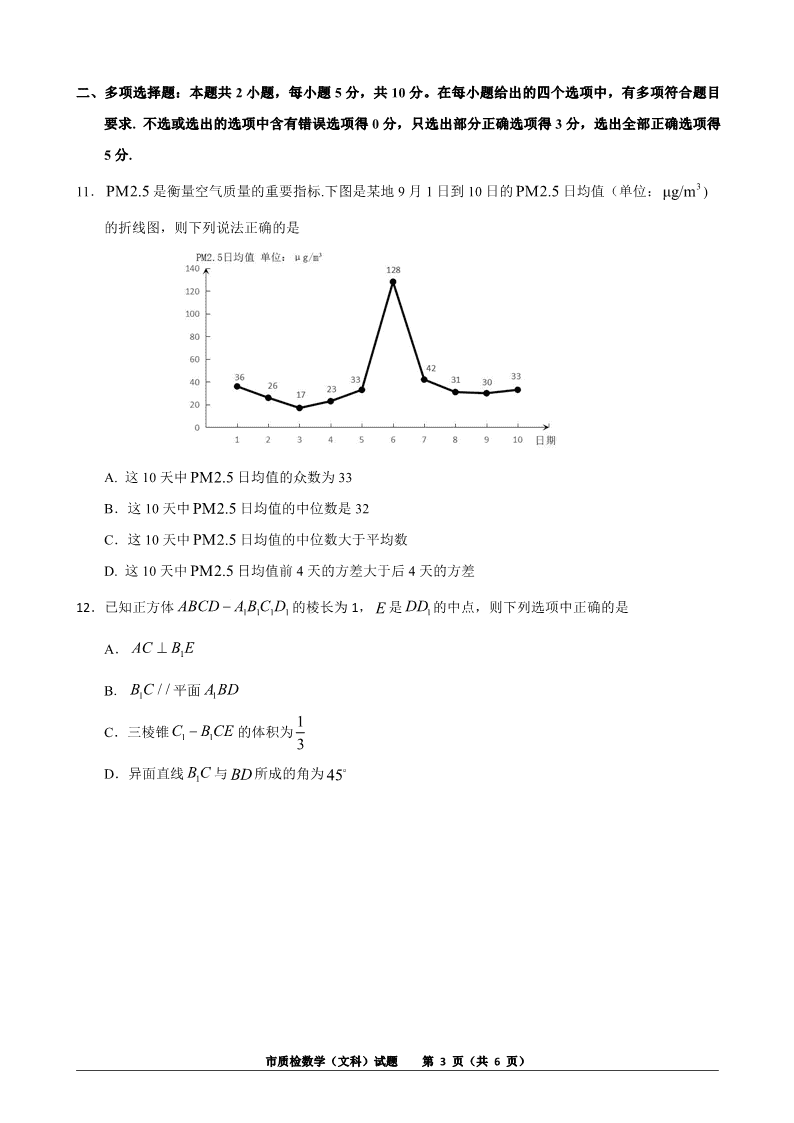11． PM2.5 是衡量空气质量的重要指标.下图是某地 9 月 1 日到 10 日的 PM2.5 日均值（单位： 3μg/m ) 的折线图，则下列说法正确的是 A. 这 10 天中 PM2.5 日均值的众数为 33 B．这 10 天中 PM2.5 日均值的中位数是 32 C．这 10 天中 PM2.5 日均值的中位数大于平均数 D. 这 10 天中 PM2.5 日均值前 4 天的方差大于后 4 天的方差 12．已知正方体 1 1 1 1ABCD A B C D- 的棱长为 1， E 是 1DD 的中点，则下列选项中正确的是 A． 1AC B E^ B. 1 / /B C 平面 1A BD C．三棱锥 1 1C B CE- 的体积为 1 3 D．异面直线 1B C 与 BD所成的角为 45 市质检数学（文科）试题 第 4 页（共 6 页） 三、填空题：本大题共 4 小题，每小题 5 分，共 20 分．将答案填在答题卡的相应位置． 13．已知向量 (1,1)a ， ( 1, )k b ， a b ，则  a b _________． 14．若函数       ,0 ,2 0,2 )( xx x xf ， 则使得不等式 0))(( aff 成立的 a 的取值范围为_____________. 15．函数 ( ) 3sin 3 cos 2f x x x   ( [0,2π])x  的最大值为 ， 所有零点之和为 ．（本题第一空 2 分，第二空 3 分） 16．正四棱柱 1 1 1 1ABCD A B C D- 中， 4AB ， 1 2 3AA = ．若 M 是侧面 11BBCC 内的动点，且 MCAM  ， 则 MA1 与平面 11BBCC 所成角的正切值的最大值为___________. 四、解答题：共 70 分．解答应写出文字说明，证明过程或演算步骤．第 17～21 题为必考题，每道试题考 生都必须作答.第 22、23 题为选考题，考生根据要求作答． （一）必考题：共 60 分. 17. （12 分） 记 nS 为数列{ }na 的前 n 项和，已知 2 nS n ，等比数列{ }nb 满足 1 1b a ， 3 5b a . （1）求{ }na 的通项公式； （2）求{ }nb 的前 n 项和 nT . 18. （12 分） 唐诗是中国文学的瑰宝.为了研究计算机上唐诗分类工作中检索关键字的选取，某研究人员将唐诗分 成 7 大类别，并从《全唐诗》48900 多篇唐诗中随机抽取了 500 篇，统计了每个类别及各类别包含“花”、 “山”、“帘”字的篇数，得到下表： 爱情婚姻 咏史怀古 边塞战争 山水田园 交游送别 羁旅思乡 其他 总计 篇数 100 64 55 99 91 73 18 500 含“山”字的篇数 51 48 21 69 48 30 4 271 含“帘”字的篇数 21 2 0 0 7 3 5 38 含“花”字的篇数 60 6 14 17 32 28 3 160 （1）根据上表判断，若从《全唐诗》含“山”字的唐诗中随机抽取一篇，则它属于哪个类别的可能 性最大，属于哪个类别的可能性最小，并分别估计该唐诗属于这两个类别的概率； 市质检数学（文科）试题 第 5 页（共 6 页） （2）已知检索关键字的选取规则为： ①若有超过95% 的把握判断“某字”与“某类别”有关系，则“某字”为“某类别”的关键字； ②若“某字”被选为“某类别”关键字，则由其对应列联表得到的 2K 的观测值越大，排名就越 靠前； 设“山”“帘”“花”和“爱情婚姻”对应的 2K 观测值分别为 1k ， 2k ， 3k .已知 0.5161 k ， 31.9622 k ， 请完成下面列联表，并从上述三个字中选出“爱情婚姻”类别的关键字并排名. 属于“爱情婚姻”类 不属于“爱情婚姻”类 总计 含“花”字的篇数 不含“花”的篇数 总计 附： 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d      ，其中 dcban  . 19. （12 分） 如图 1，四边形 ABCD 是边长为 2 的菱形， 60BAD  。，E 为CD 的中点，以 BE 为折痕将 BCE 折起到 PBE 的位置，使得平面 PBE 平面 ABCD ，如图 2. （1）证明：平面 PAB  平面 PBE ； （2）求点 D 到平面 PAB的距离. 2( )P K k≥ 0.05 0.025 0.010 k 3.841 5.024 6.635 市质检数学（文科）试题 第 6 页（共 6 页） 20. （12 分） 已知 F 是抛物线 2: 2 ( 0)C y px p  的焦点，点 A 在C 上， A 到 y 轴的距离比| |AF 小 1． （1）求C 的方程； （2）设直线 AF 与C 交于另一点 B , M 为 AB 的中点，点 D 在 x 轴上， DA DB ． 若 6DM  ，求直线 AF 的斜率． 21. （12 分） 已知函数 xaxxexf x 2sin)( 2  ． （1）当 0a 时，判断 )(xf 在 ),0[  上的单调性并加以证明； （2）若 x ≥ 0 ， )(xf ≥1，求 a 的取值范围. （二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答，并在答题卡中涂上你所选的题号. 如果 多做，则按所做的第一题计分. 22．［选修 4—4：坐标系与参数方程］（10 分） 在平面直角坐标系 xOy 中，已知直线 l 的参数方程为 , 4 3 x t y t    （ t 为参数），圆 C 的方程为 2 2( 1) 1x y   ．以坐标原点O 为极点， x 轴正半轴为极轴建立极坐标系． （1）求l 和C 的极坐标方程； （2）过 O 且倾斜角为 的直线与l 交于点 A ，与C 交于另一点 B ．若 π 5π 6 12 ≤ ≤ ， 求 OB OA 的取值范围． 23．［选修 4—5：不等式选讲］（10 分） 记函数 1( ) 2 12f x x x    的最小值为 m ． （1）求 m 的值； （2）若正数 , ,a b c 满足 abc m ，证明： 9ab bc ca a b c      ． 市质检数学（文科）参考答案与评分标准 第 1 页（共 10 页） 泉州市 2020 届普通高中毕业班第一次质量检查 数学（文科）参考答案与评分标准 评分说明： 1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考 查内容比照评分标准制定相应的评分细则． 2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难 度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部 分的解答有较严重的错误，就不再给分． 3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数．选择题和填空题不给中间分． 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分．将答案填在答题卡的相应位置。 13．2 14． ),0[  15． 2 3 2 ，14π 3 16．2. 三、解答题：共 70 分。解答应写出文字说明，证明过程或演算步骤。第 17～21 题为必考题，每个试题考 生都必须作答。第 22、23 题为选考题，考生根据要求作答。 （一）必考题：共 60 分。 17．【命题意图】本题主要考查数列 na 与 nS 的关系、等比数列的通项公式、前 n 项和公式等基础知识，考 查运算求解能力，考查化归与转化思想、分类与整合思想，考查发展数学抽象、数学运 算及数学建模等核心素养． 解：（1）当 1n  时， 1 1 1a S  ，······················································································· 1 分 当 2n≥ 时， 1n n na S S   ······················································································ 2 分 2 2( 1)n n   ·················································································· 3 分 2 1n  ，······················································································· 4 分 因为 1 1a  适合上式，·························································································5 分 所以 2 1na n  ( N )n  ．················································································· 6 分 （2）由（1）得 1 1b  ， 3 9b  ，················································································ 7 分 设等比数列{ }nb 的公比为 q ，则 2 3 1 9b b q   ，解得 3q   ．··································8 分 市质检数学（文科）参考答案与评分标准 第 2 页（共 10 页） 当 3q  时， 1 (1 3 ) 3 1 1 3 2 2 n n nT     ，······························································· 10 分 当 3q   时， 1 [1 ( 3) ] 1 ( 3) 1 ( 3) 4 4 n n nT        ．····················································· 12 分 17 评分补充说明： （1）问： ①“因为 11 a 适合上式”这句话没写不扣分；但如果没有求 11 a 的，要扣 1 分； ②用不完全归纳法求出 12  nan 的，得 3 分； （2）问： ①如果只求出 3q ，后面只求出 2 13  n nT 一种情况的，得 3 分； ②如果因为第 1 问出错，导致求的 nb 也出错，但后续解法正确的话，根据实际情况，给不超过 3 分。 18．【命题意图】本题考查统计图表、频率与概率的关系、用样本估计总体、独立性检验等知识点．考查 了学生对统计图表的识读与计算能力，考查了学生的数学建模、数据分析、数学抽象、 数学运算等核心素养． 解：（1）由上表可知， 该唐诗属于“山水田园”类别的可能性最大，属于“其他”类别的可能性最小························· 2 分 属于“山水田园”类别的概率约为 271 69 ；属于“其他”类别的概率约为 271 4 ；························ 4 分 说明：可能性最大，最小，两个概率各 1 分； 概率算错，不影响可能性判断的得分； （2）列联表如下： 属于“爱情婚姻”类 不属于“爱情婚姻”类 共计 含“花”的篇数 60 100 160 不含“花”的篇数 40 300 340 共计 100 400 500 ······································································································································ 8 分 说明：1.红色部分，一空 1 分； 2.“共计”部分算错不扣分； 市质检数学（文科）参考答案与评分标准 第 3 页（共 10 页） 计算得： 037.45160340400100 40001500 2 3  k ； ····················································· 10 分 因为 2k ， 3 3.841k  , 1 3.841k  ，所以有超过95% 的把握判断“花”字和“帘”字均与“爱情婚姻” 有关系，故“花”和“帘”是“爱情婚姻”的关键字，而“山”不是； 又因为 32 kk  ，故选择“花”，“帘”作为“爱情婚姻”类别的关键字，且排序为“花”，“帘”．···12 分 说明：1.只答“花”和“帘”，未答”山“不是，不扣分； 2.k3 算错，2 分不给，但是后续对于“帘”是关键字和“山”不是关键字作出正确判断仍给 1 分； 19．【命题意图】本题考查空间面面垂直的的判定、线面角、二面角及点到面的距离等基础知识；考查空 间想象能力、推理论证能力、运算求解能力；考查化归与转化的思想；考查直观想象、 逻辑推理和数学运算核心素养． 解法一：（1）依题意知，因为CE BE ，所以 PE BE ． 又平面 PBE 平面 ABCD ，平面 PBE  平面 ABCD BE= ， PE  平面 PBE ， 所以 PE  平面 ABCD ． ···············································································2 分 又 AB  平面 ABCD ， 所以 PE AB ． ··························································································· 3 分 由已知， BCD 是等边三角形，且 E 为CD 的中点，所以 BE CD ． 因为 CDAB // ，所以 AB BE ． ···································································4 分 又 PE BE E  ，所以 AB 平面 PBE ． ·························································5 分 又 AB  平面 PAB，所以平面 PAB  平面 PBE ． ··············································6 分 （2）在 ABD 中， 2AB AD= = ， 60BAD  。，所以 3ABDS  ．····························· 7 分 由（1）知， PE  平面 ABD ，且 1PE = ， 所以三棱锥 P ABD- 的体积 1 33 13 3V     ．····················································· 9 分 市质检数学（文科）参考答案与评分标准 第 4 页（共 10 页） 在 RT PBE 中， 1PE = ， 3BE = ，得 2PB = ． 由（1）知， AB 平面 PBE ，所以 AB PB ． 所以 2ABPS  ． ····························································································· 11 分 设点 D 到平面 PAB的距离 d ． 则三棱锥 E PAB- 的体积 1 323 3V d     ，得 3 2d = ． ·····································12 分 解法二：（1）同解法一；·····································································································6 分 （2）因为 ABDE // ， AB  平面 PAB， DE  平面 PAB， 所以 / /DE 平面 PAB． 所以点 E 到平面 PAB的距离等于点 D 到平面 PAB的距离．·······································8 分 过点 E 作 PB 的垂线，垂足 F ，即 EF PB ． 由（1）知，平面 PAB  平面 PBE ，平面 PAB 平面 PBE PB= ， EF  平面 PBE ， 所以 EF  平面 PAB，即 EF 为点 D 到平面 PAB的距离．······································ 10 分 由（1）知， PE BE ， 在 RT PBE 中， 1PE = ， 3BE = ，得 2PB = ． 又 PE BE PB EF   ，所以 3 2EF = ． 所以点 D 到平面 PAB的距离为 2 3 ．·······································································12 20．【命题意图】本小题主要考查抛物线的定义，直线与抛物线的位置关系等基础知识，考查推理论证能 力、运算求解能力等，考查化归与转化思想、数形结合思想、函数与方程思想等，考查 逻辑推理、直观想象、数学运算等核心素养，体现基础性、综合性与创新性． 解：（1）设C 的准线为l ，过 A 作 AH l 于 H ，则由抛物线定义，得| | | |AF AH ， 因为 A 到 F 的距离比到 y 轴的距离大 1，所以 12 p  ，解得 2p  ， 所以 C 的方程为 2 4y x ·························································································3 分 （2）由题意，设直线 AF 方程为 ( 1y k x  ），······························································· 4 分 市质检数学（文科）参考答案与评分标准 第 5 页（共 10 页） 由 2 ( 1), 4 , y k x y x     消去 y ，得 2 2 2 22 +4 0k x k x k  （ ） ， ··········································5 分 设 1 1 2 2( , ), ( , )A x y B x y ，则 2 1 2 2 2 +4kx x k   ，··························································· 6 分 所以 1 2 1 2 4( ) 2y y k x x k k      ， 又因为 M 为 AB 的中点，点 M 的坐标为 2 2 +2 2)k k k （ ， ，·················································7 分 直线 DM 的方程为 2 2 2 1 2( )ky xk k k     ，···························································· 8 分 令 0y  ，得 2 23x k   ，点 D 的坐标为 2 2(3 ,0)k  ，················································· 9 分 所以 2 2 2 2 42 4 6DM k k         ，···························································· 11 分 解得 2 2k  ，所以直线 AF 的斜率为 2 .······························································· 12 分 21．【命题意图】本小题主要考查导数的综合应用，利用导数研究函数的单调性、最值和零点等问题，考 查抽象概括、推理论证、运算求解能力，考查化归与转化思想、分类与整合思想、函数 与方程思想、数形结合思想、有限与无限思想以及特殊与一般思想，考查数学抽象、逻 辑推理、直观想象、数学运算、数学建模等核心素养，考查应用意识与创新意识． 解：（1）当 0a 时，   2cose  xxf x ．········································································ 1 分 记    xfxg  ，则   xxg x sine  ， 当 0x 时， 1sin1,1e  xx ．·········································································· 2 分 所以   0sine  xxg x ，所以  xg 在 ，0 单调递增，所以     00  gxg ．·········· 3 分 因为    xfxg  ，所以   0 xf ，所以  xf 在 ，0 为增函数．······························4 分 出现以下情况酌情给分： ①当 0a 时，   2cose  xxf x ．.............................1 分 没有过程，直接判断  xf 在 ，0 为增函数....................2 分 ②导函数求错,直接判断  xf 在 ，0 为增函数....................1 分 市质检数学（文科）参考答案与评分标准 第 6 页（共 10 页） ③   2cose  xxf x .............................1 分 分别作 xyey x cos221  与 的图象,由图象得到 21 yy  恒成立,但没有充足的理由 最后判断  xf 在 ，0 为增函数....................3 分 （2）由题意，得   22cose  axxxf x ，记    xfxg  ，则   axxg x 2-sine  ， 令       xxhxgxh x cose,  则 ， 当 0x≥ 时， e 1,cos 1x x≥ ≤ ，所以 ( ) e cos 0xh x x   ≥ ，·········································6 分 所以  xh 在 ，0 为增函数，即   axxg x 2-sine  在 ，0 单调递增， 所以     00 e sin 0 2 1 2g x g a a      ≥ ．························································ 7 分 ①当 2 1021  aa ， ，   0 xg 恒成立，所以  xg 为增函数，即  xf  在 ，0 单调递增， 又   00 f ，所以   0 xf ,所以  xf 在 ，0 为增函数,所以     10  fxf 所以 2 1a 满足题意．······················································································9 分 ②当 2 1a ，   ,02-10  ag 令 0,1e)(  xxxu x ， 因为 0x  ，所以 ( ) e 1 0xu x    ，故 )(xu 在 ),0(  单调递增， 故 0)0()( uxu ，即 1e xx .·············································································10 分 故   022sin1222sine2 2  aaaaaag a ， 又   axxg x 2-sine  在  ，0 单调递增， 由零点存在性定理知，存在唯一实数  0m  ， ，   0g m  ， 当  0,x m 时，   0g x  ，  xg 单调递减，即  xf  单调递减， 所以     00  fxf ，此时  xf 在  m,0 为减函数， 所以     00  fxf ,不合题意，应舍去． 综上所述， a 的取值范围是 2 1a ．····································································· 12 分 出现以下情况酌情给分(扣除第一步 4 分)： 市质检数学（文科）参考答案与评分标准 第 7 页（共 10 页） 分离参数法:当 1010  ax 时， 成立 当 2 12sin,0 x xxeax x  恒成立.......................5 分 分析函数   2 12sin x xxexg x  单调性....................9 分 (对右边函数  xg 求导,分析函数单调性,没有完整,酌情给 1 或 2 分) 求出  xg 的最大值 2 1 .....................................................11 分 所以 a 的取值范围是 2 1a ．..........................................12 分 （二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答，如果多做，则按所做的第一题计分。 22．［选修 4—4：坐标系与参数方程］ 【命题意图】本小题主要考查圆的直角坐标方程与极坐标方程的互化，直线的参数方程及参数的几何意义、 直线与圆的位置关系等基础知识，考查推理论证能力与运算求解能力，考查函数与方程思想、 化归与转化思想、数形结合思想，考查直观想象、逻辑推理、数学运算等核心素养，体现基 础性与综合性． 解：（1）因为 , 4 3 x t y t    ，所以l 的普通方程为 3 4 0x y   ，···········································1 分 又 2 2 2cos , sin ,x y x y        ， l 的极坐标方程为 3 cos sin 4 0      ，·························································· 3 分 C 的方程即为 2 2 2 0x y y   ，对应极坐标方程为 2sin  ． ································· 5 分 （2）由己知设 1 2( , ), ( , )A B    ，则 1 4 , 3 cos sin      2 2sin  ， ······················· 6 分 所以， || || OA OB 2 1 | | 1 12sin ( 3 cos sin ) [ 3sin 2 cos2 1]| | 4 4 OA OB             ·················7 分 1[2sin(2 ) 1]4 6    ······························································· 8 分 又 5 6 12    ， 226 6 3      ， 当 2 6 6     ，即 6   时， || || OA OB 取得最小值 1 2 ；················································· 9 分 市质检数学（文科）参考答案与评分标准 第 8 页（共 10 页） 当 2 6 2     ，即 3   时， || || OA OB 取得最大值 3 4 ．················································10 分 所以， || || OA OB 的取值范围为 1 3[ , ]2 4 ．········································································ 10 分 23．［选修 4—5：不等式选讲］ 【命题意图】本小题主要考查绝对值不等式的解法、不等式解集的概念、绝对值的意义等基础知识，考查 抽象概括能力、运算求解能力，考查分类与整合的思想，化归与转化的思想，考查逻辑运算、 数学运算、直观想象等核心素养，体现基础性与综合性． 解法一 ：（1）               .2 1,2 13 2 1 2 1,2 3 2 1,2 13 xx xx xx xf ， ， ·········································································· 2 分 当 2 1x 时，   22 1      fxf ， 当 2 1 2 1  x ，   12 1      fxf ， 当 2 1x 时，   12 1      fxf ，········································································4 分 所以   1min  xfm ·························································································5 分 补充：解法二 ：（1）               .2 1,2 13 2 1 2 1,2 3 2 1,2 13 xx xx xx xf ， ， ································································· 2 分 如图··································································································4 分 对 1 个给 1 分，全对 2 分 对 1 个给 1 分，全对 2 分 对 1 个给 1 分，全对 2 分 市质检数学（文科）参考答案与评分标准 第 9 页（共 10 页） 当 1 2x  时，   1min  xfm ·································································5 分 解法三 ：（1） 1 1 1 1 1 1( ) 2 2 2 2 2 2                     ≥f x x x x x x x ································1 分 11 12    ≥x ························································································2 分 当且仅当 1 1 02 2 1 =02           ≤x x x 即 1= 2x 时，等号成立. ········································· 4 分 (列式 1 分，x 值 1 分，或直接给出 x 值，2 分) 当 1 2x  时，   1min  xfm ··········································································· 5 分 解法一：（2）由题意可知， baccabcab 111  ，·····························································6 分 因为 0, 0, 0  a b c ， 所以要证明不等式 9ab bc ca a b c      ， 只需证明   9111  cbabac ）（ ，·································································7 分 因为   9313111 33  abcabccbabac ）（ 成立，·········································· 9 分 所以原不等式成立.························································································· 10 分 解法二：（2）因为 03,0,0,0 3 222  cbacabcabcba 所以 ,······································ 6 分 033  abccba ，·················································································· 7 分 又因为 1abc , 所以    933 3 2223  cbaabcacbcabcba ，········································· 8 分    9    ≥ab bc ac a b c ············································································ 9 分 所以 9ab bc ca a b c      ，原不等式得证.····················································· 10 分 补充：解法三：（2）由题意可知， baccabcab 111  ，····················································6 分 因为 0, 0, 0  a b c ， 所以要证明不等式 9ab bc ca a b c      ， 两个基本不等式各 1 分 踩空回补 市质检数学（文科）参考答案与评分标准 第 10 页（共 10 页） 只需证明  1 1 1 9       ≥a b ca b c ，······················································ 7 分 由柯西不等式得：   21 1 1 1 1 1+ + 9               ≥a b c a b ca b c a b c 成 立，·····································································································9 分 所以原不等式成立.················································································ 10 分 柯西 2 分