2021届高考数学一轮复习第七章解析几何第8讲轨迹与方程课件 36页

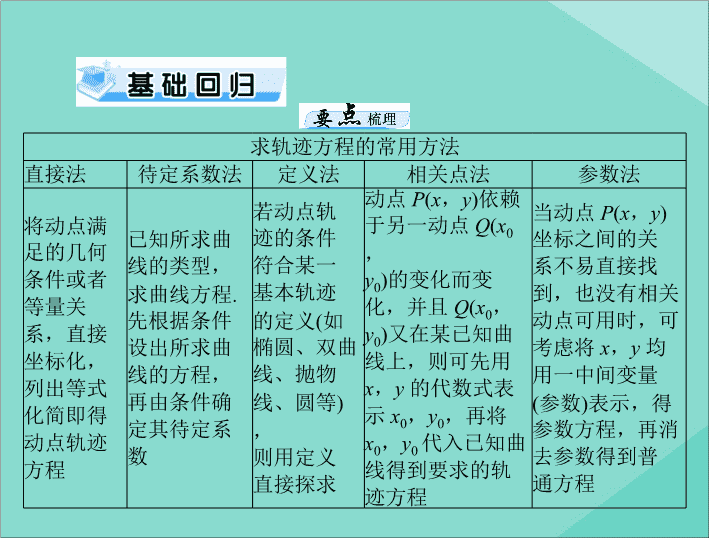
第 8 讲 轨迹与方程 课标要求 考情风向标 1. 经历从具体情境中抽象出 椭圆、抛物线模型的过程， 掌握它们的定义、标准方程、 几何图形 . 2. 了解双曲线的定义、几何图 形和标准方程 . 3. 结合已学过的曲线及其方 程的实例，了解曲线与方程 的对应关系，进一步感受数 形结合的基本思想 求曲线 ( 或轨迹 ) 的方程，对于这 类 问题，高考常常不给出图形或不 给出坐标系，以考查理解解析几 何问题的基本思想方法和能力 . 备 考时要关注以下几点： (1) 能够利用定义或待定系数法求 椭圆、双曲线及抛物线的方程 . (2) 能够利用相 关点法、参数法等 求动点的轨迹方程 求轨迹方程的常用方法 直接法 待定系数法 定义法 相关点法 参数法 将动点满 足的几何 条件或者 等量关 系，直接 坐标化， 列出等式 化简即得 动点轨迹 方程 已知所求曲 线的类型， 求曲线方程 . 先根据条件 设出所求曲 线的方程， 再由条件确 定其待定系 数 若动点轨 迹的条件 符合某一 基本轨迹 的定义 ( 如 椭圆、双曲 线、抛物 线、圆等 ) ， 则用定义 直接探求 动点 P ( x ， y ) 依赖 于另一动点 Q ( x 0 ， y 0 ) 的变化而变 化，并且 Q ( x 0 ， y 0 ) 又在某已知曲 线上 ，则可先用 x ， y 的代数式表 示 x 0 ， y 0 ，再将 x 0 ， y 0 代入已知曲 线得 到要求的轨 迹方程 当动点 P ( x ， y ) 坐标之间的关 系不易直接找 到，也没有相关 动点可用时，可 考虑将 x ， y 均 用一中间变量 ( 参数 ) 表示，得 参数方程，再消 去参数得到普 通方程 解析： ∵ | BC | ， | CA | ， | AB | 成等差数列， ∴| BC | ＋ | BA | ＝ 2| CA | ＝ 4. ∴ 点 B 的轨迹是以 A ， C 为焦点，半焦距 c ＝ 1 ，长轴长 2 a ＝ 4 的椭圆 . 又 B 是三角形的顶点， A ， B ， C 三点不能共线， 答案： D A C B D 答案： D D 4.(2019 年云南质量检测 ) 已知 M ( － 2 ,0) ， N (2,0) ，则以 MN 为斜边的直角三角形的直角顶点 P 的轨迹方程为 ( ) D 考点 1 利用直接法求轨迹方程 例 1 ： (1) 如图 7-8-1 ，已知点 C 的坐标是 (2,2) ，过点 C 的直 线 CA 与 x 轴交于点 A ，过点 C 且与直线 CA 垂直的直线 CB 与 y 轴交于点 B . 设点 M 是线段 AB 的中点，则点 M 的轨迹方程为 ________. 图 7-8-1 两式相加，得 x 0 ＋ y 0 ＝ 2 ，即 x 0 ＋ y 0 － 2 ＝ 0( x 0 ≠1). 又点 (1,1) 在直线 x 0 ＋ y 0 － 2 ＝ 0 上， ∴ 点 M 的轨迹方程为 x ＋ y － 2 ＝ 0. M 到点 C ， O 的距离相等，故点 M 在线段 OC 的垂直平分线上 . 又线段 OC 的垂直平分线过 OC 中点 (1,1) ，斜率 k ＝－ 1 ， 即 y － 1 ＝－ ( x － 1) ，化简，得 x ＋ y － 2 ＝ 0. ∴ 点 M 的轨迹方程为 x ＋ y － 2 ＝ 0. 答案： x ＋ y － 2 ＝ 0 A. x 2 ＝ 4 y C. x 2 ＝ 2 y B. y 2 ＝ 3 x D. y 2 ＝ 4 x 解析： 设 P ( x ， y ) ，则 Q ( x ，－ 1). ∴(0 ， y ＋ 1)·( － x, 2) ＝ ( x ， y － 1)·( x ，－ 2) ， 即 2( y ＋ 1) ＝ x 2 － 2( y － 1) ，整理得 x 2 ＝ 4 y . ∴ 动点 P 的轨迹 C 的方程为 x 2 ＝ 4 y . 答案： A 【 规律方法 】 求轨迹的步骤是 “建系、设点、列式、化简”， 建系的原则是特殊化 ( 把图形放在最特殊的位置上 ) ，这类问题 一般需要通过对图形的观察、分析、转化，找出一个关于动点 的等量关系 . 考点 2 利用定义法求轨迹方程 例 2 ： (1) 已知圆 C 1 ： ( x ＋ 3) 2 ＋ y 2 ＝ 1 和圆 C 2 ： ( x － 3) 2 ＋ y 2 ＝ 9 ， ① 动圆 M 同时与圆 C 1 及圆 C 2 相外切，则动圆圆心 M 的轨 迹方程为 __________________ ； ② 若动圆 M 同时与圆 C 1 及圆 C 2 相内切，则动圆圆心 M 的 轨迹方程为 ________________ ； ③ 若动圆 M 与圆 C 1 外切及圆 C 2 相内切，则动圆圆心 M 的 轨迹方程为 ________________ ； ④ 若动圆 M 与圆 C 1 内切及圆 C 2 相外切，则动圆圆心 M 的 轨迹方程为 ________________. 解析： 如图 D60 ，设动圆 M 与圆 C 1 及圆 C 2 分别外切于点 A 和点 B ，根据两圆外切的充要条件，得 | MC 1 | － | AC 1 | ＝ | MA | ， | MC 2 | － | BC 2 | ＝ | MB |. ∵| MA | ＝ | MB | ， ∴| MC 2 | － | MC 1 | ＝ | BC 2 | － | AC 1 | ＝ 3 － 1 ＝ 2. 图 D60 这表明动点 M 到两定点 C 2 ， C 1 的距离之差是常数 2. (2) 已知圆 ( x ＋ 2) 2 ＋ y 2 ＝ 1 的圆心为 M ，设 A 为圆上任一点， N (2,0) ，线段 AN 的垂直平分线交直线 MA 于点 P ，则动点 P 的 轨迹是 ( ) A. 圆 B. 椭圆 C. 双曲线 D. 抛物线 解析： 点 P 在线段 AN 的垂直平分线上，故 | PA | ＝ | PN |. 又 AM 是圆的半径， ∴| PM | － | PN | ＝ | PM | － | PA | ＝ | AM | ＝ 1<| MN |. 由双曲线的定义 知，点 P 的轨迹是双曲线 . 答案： C 图 D61 ① 分别过点 E ( － c, 0) ， F ( c, 0) ，作 ⊙ C 1 的不同于 x 轴的切线， 两切线相交于点 M ，则点 M 的轨迹为椭圆的一部分； ② 若 ⊙ C 1 ， ⊙ C 2 相切于点 H ，则点 H 的轨迹恒在定圆上； ③ 若 ⊙ C 1 ， ⊙ C 2 相离，且 r 1 ＝ 2 r 2 ＝ a ，则与 ⊙ C 1 ， ⊙ C 2 都 外切的圆的圆心在定椭圆上 . 则以上命题正确的是 ( ) A.①② B.①③ C.②③ D.①②③ 解析： 对于 ① ，如图 D62 ， | ME | ＋ | MF | ＝ | ML | ＋ | LE | ＋ | MF | ＝ | MN | ＋ | AE | ＋ | MF | ＝ | AE | ＋ | NF | ＝ | AE | ＋ | AF | ＝ 2 a ，故点 M 恒在 以 E ， F 为焦点， AB 为长轴的椭圆上， ① 正确； 图 D62 图 D63 对于 ② ，若 ⊙ C 1 与 x 轴相切于点 A ， ⊙ C 2 与 x 轴相切于点 B ，由题意，知 ⊙ C 1 ， ⊙ C 2 相外切，且 ⊙ C 1 ， ⊙ C 2 相切于点 H ， 过点 H 作两圆公切线，交 x 轴于点 Q ，如图 D63 ，则 | QA | ＝ | QH | ＝ | QB | ，故 Q 与 O 点重合 .∴| QH | ＝ a ，故点 H 的轨迹恒在定圆 上， ② 正确； 答案： A 考点 3 利用相关点法求轨迹方程 A. 直线 C. 椭圆 B. 圆 D. 双曲线 答案： A 【 规律方法 】 动点 P ( x ， y ) 依赖于另一动点 Q ( x 0 ， y 0 ) 的变化 而变化，并且 Q ( x 0 ， y 0 ) 又在某已知曲线上，则可先用 x ， y 的代 数式表示 x 0 ， y 0 ，再将 x 0 ， y 0 代入已知曲线方程得出要求的轨 迹方程 . 这种求轨迹方程的方法叫做相关点法 ( 也叫做转移法 ). 【 跟踪训练 】 思想与方法 ⊙ 轨迹方程中的分类 讨论 例题： 已知 A ， B 为平面内两定点，过该平面内动点 M 作 ) 则动点 M 的轨迹不可能是 ( A. 圆 C. 抛物线 B. 椭圆 D. 双曲线 解析： 以 AB 所在直线为 x 轴， AB 的中垂线为 y 轴，建立 平面直角坐标系， 设 M ( x ， y ) ， A ( － a, 0) ， B ( a, 0) ，则 N ( x, 0). ∴ y 2 ＝ λ ( x ＋ a )( a － x ) ，即 λx 2 ＋ y 2 ＝ λa 2 . 当 λ ＝ 1 时，轨迹是圆； 当 λ ＞ 0 且 λ ≠1 时，轨迹是椭圆； 当 λ ＜ 0 时，轨迹是双曲线； 当 λ ＝ 0 时，轨迹是直线 . 综上，动点 M 的轨迹不可能是抛物线 . 答案： C 【 跟踪训练 】 2.(2019 年北京 ) 数学中有许多形状优美、寓意美好的曲线， 曲线 C ： x 2 ＋ y 2 ＝ 1 ＋ | x | y 就是其中之一 ( 如图 7-8-2). 给出下列三 个结论： ① 曲线 C 恰好经过 6 个整点 ( 即横、纵坐标均为整 数的点 ) ； ③ 曲线 C 所围成的“心形”区域的面积小于 3. 图 7-8-2 其中，所有正确结论的序号是 ( ) A.① B.② C.①② D.①②③ 如图 D65 ，易知 A (0 ，－ 1) ， B (1,0) ， C (1,1) ， D (0,1) ， 图 D65 “ 心形”区域的面积大于 2 S 四边形 ABCD ，即“心形”区域的面积 大于 3 ，说法 ③ 错误 . 故选 C. 答案： C 求轨迹方程的常用方法 (1) 直接法：根据题目条件，直译为关于动点的几何关系， 再利用解析几何有关公式 ( 两点距离公式、点到直线距离公式、 夹角公式等 ) 进行整理、化简，即把这种关系“翻译”成含 x ， y 的等式就得到曲线的轨迹方程了 . (2) 定义法：若动点轨迹满足已知曲线的定义，可先设定方 程，再确定其中的基本量，求出动点的轨迹方程 . (3) 相关点法：有些问题中，其动点满足的条件不便用等式 列出，但动点是随着另一动点 ( 称之为相关点 ) 而运动的，如果 相关点所满足的条件是明显的，或是可分析的，这时我们可以 用动点坐标表示相关点坐标，根据相关点所满足的方程即可求 得动点的轨迹方程 .