- 242.00 KB
- 2021-06-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
【考向解读】
1.以客观题形式考查算法的基本逻辑结构,会与函数、数列、不等式、统计、概率等知识结合命题.
2.以客观题形式考查复数的运算、复数的相等、共轭复数和复数及其代数运算的几何意义,与其他知识较少结合,应注意和三角函数结合的练习.
3.推理与证明在选择、填空、解答题中都有体现,但很少单独命题,若单独命题,一般以客观题形式考查归纳与类比.
4.通常是以数列、三角、函数、解析几何、立体几何等知识为载体,考查对推理与证明的掌握情况,把推理思路的探求、推理过程的严谨,推理方法的合理作为考查重点.
【命题热点突破一】程序框图
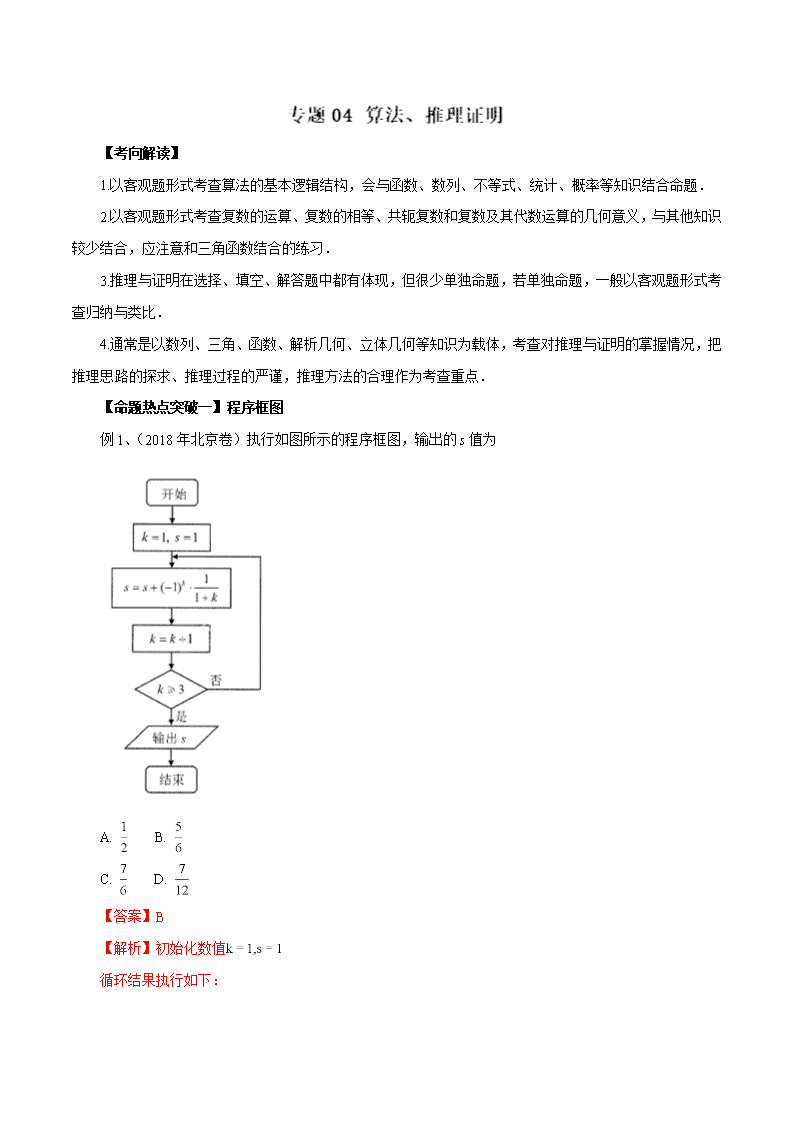
例1、(2018年北京卷)执行如图所示的程序框图,输出的s值为
A. B.
C. D.
【答案】B
【解析】初始化数值
循环结果执行如下:
第一次:不成立;
第二次:成立,
循环结束,输出,故选B.
【变式探究】(1)观察下列各式:
C=40;
C+C=41;
C+C+C=42;
C+C+C+C=43;
……
照此规律,当n∈N*时,
C+C+C+…+C=________.
(2)我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法可以求出过点A(-2,3),且法向量为n=(-1,2)的直线方程为(-1)×(x+2)+2×(y-3)=0,化简得x-2y+8=0.类比上述方法,在空间直角坐标系中,经过点A(1,2,3),且法向量为n=(-1,2,-3)的平面的方程为________.
【答案】(1)4n-1 (2)x-2y+3z-6=0
【感悟提升】由特殊结论得出一般结论的推理是归纳推理,归纳出的一般性结论要包含已知的特殊结论;根据已有结论推断相似对象具有相应结论的推理就是类比推理.归纳和类比得出的结论未必正确,其正确性需要通过演绎推理进行证明.合情推理和演绎推理在解决数学问题中是相辅相成的.
【变式探究】
已知cos=,coscos=,coscos·cos=,……根据以上等式,可猜想的一般结论是________________.
【答案】coscos…cos=(n∈N*)
【解析】从已知等式的左边来看,3,5,7,…是通项为2n+1的等差数列,等式的右边是通项为
的等比数列.由以上分析可以猜想出一般结论为coscos…cos=(n∈N*).
4. (2018年天津卷)阅读如图所示的程序框图,运行相应的程序,若输入的值为20,则输出的值为
A. 1 B. 2 C. 3 D. 4
【答案】B
1. 【2017山东,文6】执行右侧的程序框图,当输入的x值为4时,输出的y的值为2,则空白判断框中的条件可能为
A. B. C. D.
【答案】B
【解析】由题意得 时判断框中的条件应为不满足,所以选B.
【考点】程序框图
2.【2017课标1,文10】如图是为了求出满足的最小偶数n,那么在和两个空白框中,可以分别填入
A.A>1000和n=n+1 B.A>1000和n=n+2
C.A≤1000和n=n+1 D.A≤1000和n=n+2
【答案】D
3.【2017课标3,文8】执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5 B.4 C.3 D.2
【答案】D
【解析】若,第一次进入循环,成立,,成立,第二次进入循环,此时,不成立,所以输出成立,所以输入的正整数的最小值是2,故选D.
7.【2017北京,文14】某学习小组由学生和
【答案】C
4.(2015·新课标全国Ⅱ,8)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )
A.0 B.2 C.4 D.14
【答案】B
5.(2015·山东,13)执行如图所示的程序框图,输出的T的值为________.
【解析】当n=1时,T=1+x1dx=1+=1+=;
当n=2时,T=+x2dx=+=+=;
当n=3时,结束循环,输出T=.
【答案】
相关文档
- 2014年辽宁省高考数学试卷(文科)2021-06-1027页
- 甘肃省张掖市第二中学2019-2020学2021-06-108页
- 河北省张家口市宣化区宣化第一中学2021-06-1012页
- 数学卷·2018届山东省临沂市临沭一2021-06-1027页
- 数学卷·2018届河北省邯郸市鸡泽一2021-06-1017页
- 2018-2019学年西藏林芝二高高一上2021-06-104页
- 河南省许昌市第三高级中学2020届高2021-06-1010页
- 福建莆田一中2012届高三数学上学期2021-06-1011页
- 四川省攀枝花市2019-2020学年高二2021-06-1011页
- 【精品试题】2021年高考数学一轮复2021-06-105页