2020高中数学 第三章 第1课时 空间向量与平行关系学案 新人教A版选修2-1 8页

第1课时　空间向量与平行关系 学习目标：1.掌握直线的方向向量，平面的法向量的概念及求法．(重点)2.熟练掌握用方向向量，法向量证明线线、线面、面面间的平行关系．(重点、难点)‎ ‎[自 主 预 习·探 新 知]‎ ‎1．直线的方向向量与平面的法向量 ‎(1)直线的方向向量的定义 直线的方向向量是指和这条直线_平行或共线的非零向量，一条直线的方向向量有无数个．‎ ‎(2)平面的法向量的定义 直线l⊥α，取直线l的方向向量a，则a叫做平面α的法向量．‎ 思考：直线的方向向量(平面的法向量)是否唯一？‎ ‎[提示]　不唯一，直线的方向向量(平面的法向量) 有无数个，它们分别是共线向量．‎ ‎2．空间中平行关系的向量表示 线线平行 设两条不重合的直线l，m的方向向量分别为a＝(a1，b1，c1)，b＝(a2，b2，c2)，则l∥m⇒a∥b⇔(a1，b1，c1)＝k(a2，b2，c2)‎ 线面平行 设l的方向向量为a＝(a1，b1，c1)，α的法向量为u＝(a2，b2，c2)，则l∥α⇔a·u＝0⇔a‎1a2＋b1b2＋c‎1c2＝0‎ 面面平行 设α，β的法向量分别为u＝(a1，b1，c1)，v＝(a2，b2，c2)，则α∥β⇔u∥v⇔(a1，b1，c1)＝k(a2，b2，c2)‎ ‎[基础自测]‎ ‎1．思考辨析 ‎(1)一个平面的单位法向量是唯一的．(　　)‎ ‎(2)一条直线的方向向量和一个平面的法向量垂直，则这条直线和这个平面平行．(　　)‎ ‎(3)若两个平面的法向量不平行，则这两个平面相交．(　　)‎ ‎[答案]　(1)×　(2)×　(3)√‎ ‎2．若A(－1,0,1)，B(1,4,7)在直线l上，则直线l的一个方向向量为(　　)‎ A．(1,2,3)　　　　 B．(1,3,2)‎ C．(2,1,3) D．(3,2,1)‎ A　[＝(2,4,6)＝2(1,2,3)．]‎ ‎3．若直线l的方向向量a＝(2,2，－1)，平面α的法向量μ＝(－6,8,4)，则直线l与平面α的位置关系是________. ‎ ‎【导学号：46342161】‎ l⊂α或l∥α　[∵μ·a＝－12＋16－4＝0，‎ 8‎ ‎∴μ⊥a，‎ ‎∴l⊂α或l∥α.]‎ ‎[合 作 探 究·攻 重 难]‎ 求平面的法向量 ‎　如图321，已知ABCD是直角梯形，∠ABC＝90°，SA⊥平面ABCD，SA＝AB＝BC＝1，AD＝，试建立适当的坐标系．‎ 图321‎ ‎(1)求平面ABCD的一个法向量；‎ ‎(2)求平面SAB的一个法向量；‎ ‎(3)求平面SCD的一个法向量．‎ ‎[解]　以点A为原点，AD、AB、AS所在的直线分别为x轴、y轴、z轴，建立如图所示的空间直角坐标系，则A(0,0,0)，B(0,1,0)，C(1,1,0)，D，S(0,0,1)．‎ ‎(1)∵SA⊥平面ABCD，‎ ‎∴＝(0,0,1)是平面ABCD的一个法向量．‎ ‎(2)∵AD⊥AB，AD⊥SA，∴AD⊥平面SAB，‎ ‎∴＝是平面SAB的一个法向量．‎ ‎(3)在平面SCD中，＝，＝(1,1，－1)．‎ 设平面SCD的法向量是n＝(x，y，z)，‎ 则n⊥，n⊥，所以 得方程组∴ 令y＝－1，得x＝2，z＝1，∴n＝(2，－1,1)．‎ 8‎ ‎[规律方法]　1.利用待定系数法求平面法向量的步骤 ‎(1)设向量：设平面的法向量为n＝(x，y，z)．‎ ‎(2)选向量：在平面内选取两个不共线向量，.‎ ‎(3)列方程组：由列出方程组．‎ ‎(4)解方程组： ‎(5)赋非零值：取其中一个为非零值(常取±1)．‎ ‎(6)得结论：得到平面的一个法向量．‎ ‎2．求平面法向量的三个注意点 ‎(1)选向量：在选取平面内的向量时，要选取不共线的两个向量．‎ ‎(2)取特值：在求n的坐标时，可令x，y，z中一个为一特殊值得另两个值，就是平面的一个法向量．‎ ‎(3)注意0：提前假定法向量n＝(x，y，z)的某个坐标为某特定值时一定要注意这个坐标不为0.‎ ‎[跟踪训练]‎ ‎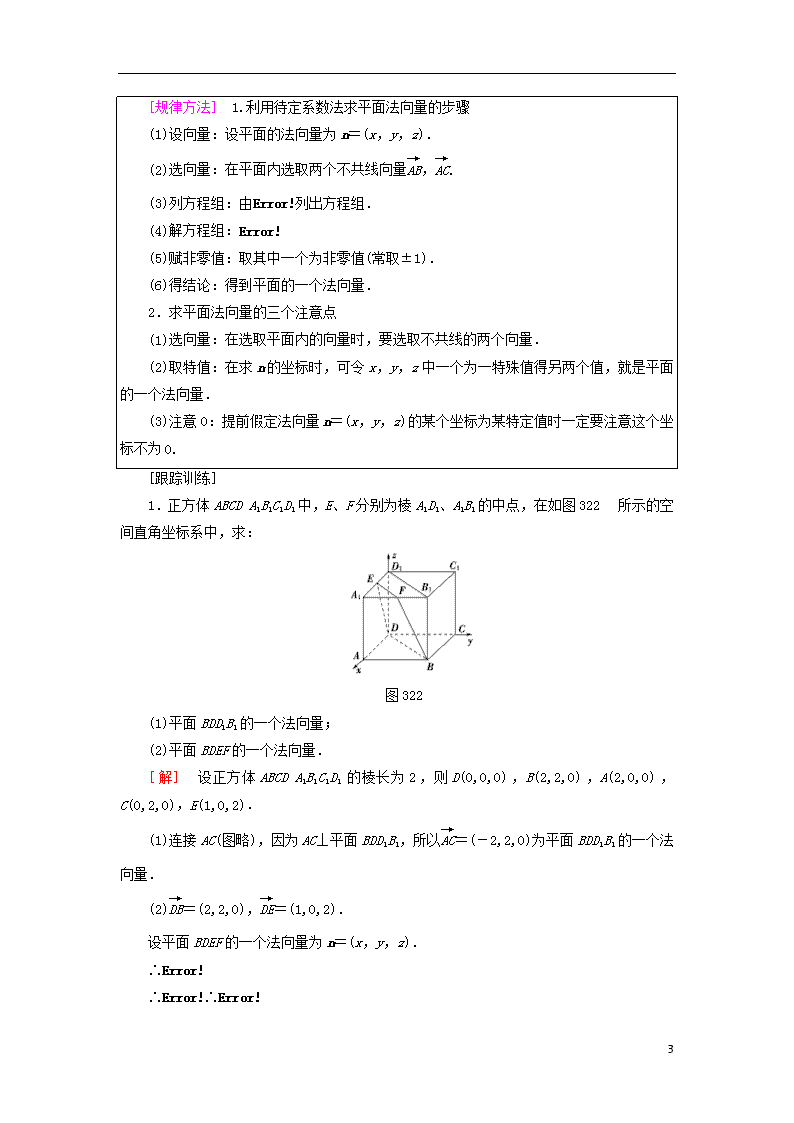1．正方体ABCDA1B‎1C1D1中，E、F分别为棱A1D1、A1B1的中点，在如图322所示的空间直角坐标系中，求：‎ 图322‎ ‎(1)平面BDD1B1的一个法向量；‎ ‎(2)平面BDEF的一个法向量．‎ ‎[解]　设正方体ABCDA1B‎1C1D1的棱长为2，则D(0,0,0)，B(2,2,0)，A(2,0,0)，C(0,2,0)，E(1,0,2)．‎ ‎(1)连接AC(图略)，因为AC⊥平面BDD1B1，所以＝(－2,2,0)为平面BDD1B1的一个法向量．‎ ‎(2)＝(2,2,0)，＝(1,0,2)．‎ 设平面BDEF的一个法向量为n＝(x，y，z)．‎ ‎∴ ‎∴∴ 8‎ 令x＝2，得y＝－2，z＝－1.‎ ‎∴n＝(2，－2，－1)即为平面BDEF的一个法向量.‎ 利用空间向量证明线线平行 ‎　如图323所示，在正方体ABCDA1B‎1C1D1中，E，F分别为DD1和BB1的中点．求证：四边形AEC‎1F是平行四边形．‎ 图323‎ ‎[解]　以点D为坐标原点，分别以，，为正交基底建立空间直角坐标系，不妨设正方体的棱长为1，则A(1,0,0)，E，C1(0,1,1)，F，‎ ‎∴＝，＝，＝，＝，‎ ‎∴＝，＝，‎ ‎∴∥，∥，‎ 又∵FAE，FEC1，∴AE∥FC1，EC1∥AF，‎ ‎∴四边形AEC‎1F是平行四边形．‎ ‎[规律方法]　1.两直线的方向向量共线(垂直)时，两直线平行(垂直)；否则两直线相交或异面．‎ ‎2．直线的方向向量与平面的法向量共线时，直线和平面垂直；直线的方向向量与平面的法向量垂直时，直线在平面内或线面平行；否则直线与平面相交但不垂直．‎ ‎3．两个平面的法向量共线(垂直)时，两平面平行(垂直)；否则两平面相交但不垂直．‎ ‎[跟踪训练]‎ 8‎ ‎2．长方体ABCDA1B‎1C1D1中，E，F分别是面对角线B1D1，A1B上的点，且D1E＝2EB1，BF＝2FA1.求证：EF∥AC1. ‎ ‎【导学号：46342162】‎ ‎[证明]　如图所示，分别以DA，DC，DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系，设DA＝a，DC＝b，DD1＝c，则得下列各点的坐标：A(a,0,0)，C1(0，b，c)，E，F.‎ ‎∴＝，＝(－a，b，c)，‎ ‎∴＝.‎ 又FE与AC1不共线，∴直线EF∥AC1.‎ 利用空间向量证明线面、面面平行 ‎[探究问题]‎ 在用向量法处理问题时，若几何体的棱长未确定，应如何处理？‎ 提示：可设几何体的棱长为1或a，再求点的坐标．‎ ‎　在正方体ABCDA1B‎1C1D1中，M，N分别是CC1，B‎1C1的中点．求证：MN∥平面A1BD．‎ ‎[思路探究]　 ‎ ‎[证明]　法一　如图，以D为原点，DA，DC，DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，设正方体的棱长为1，则D(0,0,0)，A1(1,0,1)，B(1,1,0)，M，N，于是＝(1,0,1)， 8‎ ‎＝(1,1,0)，＝.‎ 设平面A1BD的法向量为n＝(x，y，z)，则即取x＝1，则y＝－1，z＝－1，∴平面A1BD的一个法向量为n＝(1，－1，－1)．‎ 又·n＝·(1，－1，－1)＝0，∴⊥n.∴MN∥平面A1BD．‎ 法二　＝－＝－＝(－)＝，∴∥，∴MN∥平面A1BD．‎ 法三　＝－＝－＝－＝－＝－.‎ 即可用与线性表示，故与，是共面向量，故MN∥平面A1BD．‎ 母题探究：1.(变条件)本例中条件不变，试证明平面A1BD∥平面CB1D1.‎ ‎[证明]　由例题解析知，C(0,1,0)，D1(0,0,1)，B1(1,1,1)，‎ 则＝(0，－1,1)，＝(1,1,0)，‎ 设平面CB1D1的法向量为m＝(x1，μ1，z1)，‎ 则，即 令y1＝1，可得平面CB1D1的一个法向量为m＝(－1,1,1)，‎ 又平面A1BD的一个法向量为n＝(1，－1，－1)．‎ 所以m＝－n，所以m∥n，故平面A1BD∥平面CB1D1.‎ ‎2．(变条件)若本例换为：‎ 在如图324所示的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC，BC＝2AD＝4，EF＝3，AE＝BE＝2，G是BC的中点，求证：AB∥平面DEG.‎ 图324‎ ‎[证明]　∵EF⊥平面AEB，AE⊂平面AEB，BE⊂平面AEB，‎ ‎∴EF⊥AE，EF⊥BE.‎ 又∵AE⊥EB，∴EB，EF，EA两两垂直．‎ 8‎ 以点E为坐标原点，EB，EF，EA分别为x轴，y轴，z轴建立如图所示的空间直角坐标系．‎ 由已知得，A(0,0,2)，B(2,0,0)，C(2,4,0)，F(0,3,0)，D(0,2,2)，G(2，2,0)，∴＝(0,2,2)，＝(2,2,0)，＝(2,0，－2)．‎ 设平面DEG的法向量为n＝(x，y，z)，‎ 则即 令y＝1，得z＝－1，x＝－1，则n＝(－1,1，－1)，‎ ‎∴·n＝－2＋0＋2＝0，即⊥n.‎ ‎∵AB⊄平面DEG，‎ ‎∴AB∥平面DEG.‎ ‎[规律方法]　1.向量法证明线面平行的三个思路 ‎(1)设直线l的方向向量是a，平面α的法向量是u，则要证明l∥α，只需证明a⊥u，即a·u＝0.‎ ‎(2)根据线面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行，要证明一条直线和一个平面平行，在平面内找一个向量与已知直线的方向向量是共线向量即可．‎ ‎(3)根据共面向量定理可知，如果一个向量和两个不共线的向量是共面向量，那么这个向量与这两个不共线的向量确定的平面必定平行，因此要证明一条直线和一个平面平行，只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可．‎ ‎2．证明面面平行的方法 设平面α的法向量为μ，平面β的法向量为v，则α∥β⇔μ∥v.‎ ‎[当 堂 达 标·固 双 基]‎ ‎1．已知向量a＝(2,4,5)，b＝(3，x，y)，a与b分别是直线l1，l2的方向向量，若l1∥l2，则(　　)‎ A．x＝6，y＝15　　　　 B．x＝3，y＝ C．x＝3，y＝15 D．x＝6，y＝ 8‎ D　[∵l1∥l2，∴a∥b，‎ ‎∴存在λ∈R，使a＝λb，‎ 则有2＝3λ，4＝λx,5＝λy，‎ ‎∴x＝6，y＝.]‎ ‎2．已知线段AB的两端点坐标为A(9，－3,4)，B(9,2,1)，则线段AB与坐标平面(　　)‎ A．xOy平行 B．xOz平行 C．yOz平行 D．yOz相交 C　[＝(0,5，－3)，坐标平面yOz的一个法向量为n＝(1,0,0)，因为·n＝0，所以⊥n.‎ 故线段AB与坐标平面yOz平行．]‎ ‎3．已知直线l的方向向量为(2，m,1)，平面α的法向量为，且l∥α，则m＝________.‎ ‎－8　[∵l∥α，∴l的方向向量与α的法向量垂直．‎ ‎∴(2，m,1)×＝2＋m＋2＝0.‎ 解得m＝－8.]‎ ‎4．在长方体OAEBO‎1A1E1B1中，OA＝3，OB＝4，OO1＝2，点P在棱AA1上，且AP＝2PA1，点S在棱BB1上，且SB1＝2BS，点Q，R分别是棱O1B1，AE的中点．求证：PQ∥RS. ‎ ‎【导学号：46342163】‎ ‎[解]　如图，建立空间直角坐标系，则A(3,0,0)，B(0,4,0)，O1(0,0,2)，A1(3,0,2)，B1(0,4,2)，E(3,4,0)．‎ 易求得P，Q(0,2,2)，R(3,2,0)，S，‎ 于是＝，＝.‎ ‎∴＝，∴∥.∵RPQ，∴PQ∥RS.‎ 8‎