2020高中数学 第一章 常用逻辑用语 1 6页

‎1.1.1　‎命题 学习目标：1.了解命题的概念．(难点)2.理解命题的构成形式，能将命题改写为“若p，则q”的形式．(重点)3.能判断一些简单命题的真假．(难点，易错点)‎ ‎[自 主 预 习·探 新 知]‎ ‎1．命题的定义与分类 ‎(1)命题的定义：在数学中，我们把用语言、符号或式子表达的，可以判断真假的陈述句叫做命题．‎ ‎(2)命题定义中的两个要点：“可以判断真假”和“陈述句”．我们学习过的定理、推论都是命题．‎ ‎(3)分类 命题 思考1：(1)“x－1＝‎0”‎是命题吗？‎ ‎(2)“命题一定是陈述句，但陈述句不一定是命题”这个说法正确吗？‎ ‎[提示]　(1)“x－1＝‎0”‎不是命题，因为它不能判断真假．‎ ‎(2)正确．根据命题的定义，命题一定是陈述句，但陈述句中只有能够判断真假的才是命题．‎ ‎2．命题的结构 ‎(1)命题的一般形式为“若p，则q”．其中p叫做命题的条件，q叫做命题的结论．‎ ‎(2)确定命题的条件和结论时，常把命题改写成“若p，则q”的形式．‎ 思考2：命题“实数的平方是非负数”的条件与结论分别是什么？‎ ‎[提示]　条件是“一个数是实数”，结论是：“它的平方是非负数”．‎ ‎[基础自测]‎ ‎1．思考辨析 ‎(1)一个命题不是真命题就是假命题． (　　)‎ ‎(2)一个命题可以是感叹句． (　　)‎ ‎(3)x>5是命题． (　　)‎ ‎[解析]　根据命题的定义知(1)正确，(2)、(3)错误．‎ ‎[答案]　(1)√　(2)×　(3)×‎ ‎2．下列语句是命题的是(　　)‎ ‎①三角形内角和等于180°；②2>3；‎ ‎③一个数不是正数就是负数；④x>2；‎ ‎⑤2018央视狗年春晚真精彩啊！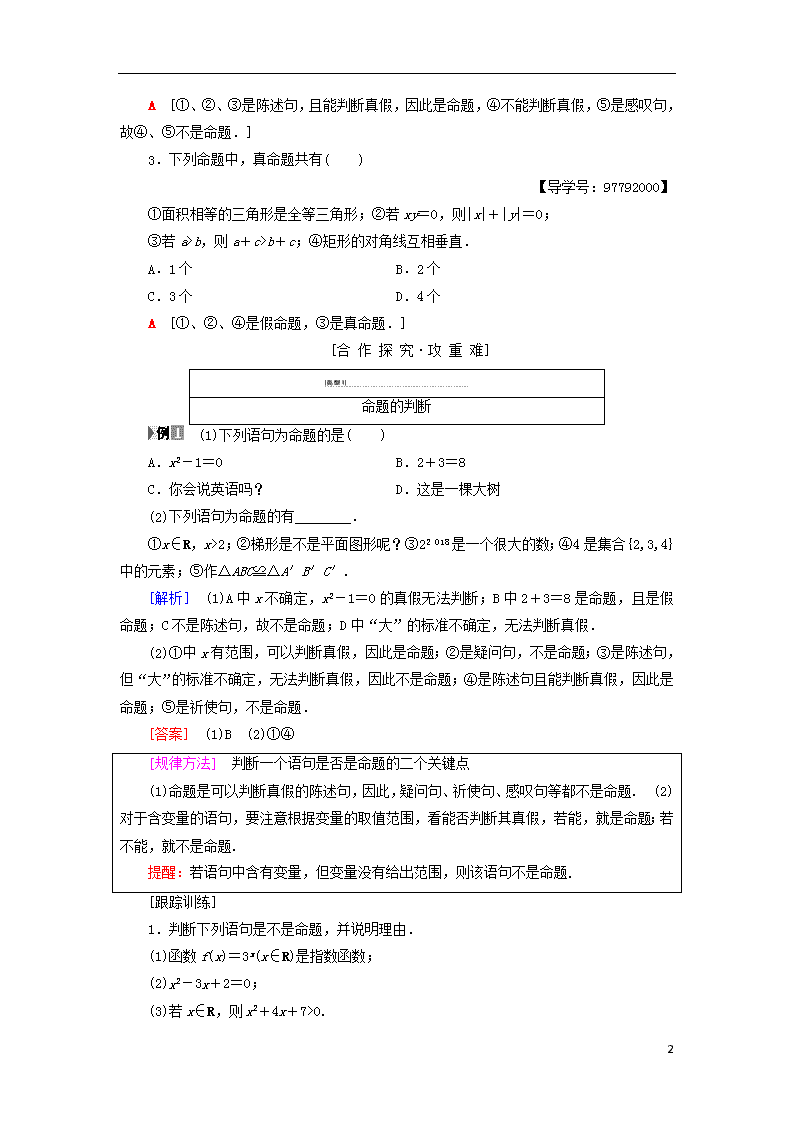‎ A．①②③　　　　　 B．①③④‎ C．①②⑤ D．②③⑤‎ 6‎ A　[①、②、③是陈述句，且能判断真假，因此是命题，④不能判断真假，⑤是感叹句，故④、⑤不是命题．]‎ ‎3．下列命题中，真命题共有(　　) ‎ ‎【导学号：97792000】‎ ‎①面积相等的三角形是全等三角形；②若xy＝0，则|x|＋|y|＝0；‎ ‎③若a>b，则a＋c>b＋c；④矩形的对角线互相垂直．‎ A．1个 B．2个 C．3个 D．4个 A　[①、②、④是假命题，③是真命题．]‎ ‎[合 作 探 究·攻 重 难]‎ 命题的判断 ‎　(1)下列语句为命题的是(　　)‎ A．x2－1＝0　　　　 B．2＋3＝8‎ C．你会说英语吗？ D．这是一棵大树 ‎(2)下列语句为命题的有________．‎ ‎①x∈R，x>2；②梯形是不是平面图形呢？③22 018是一个很大的数；④4是集合{2,3,4}中的元素；⑤作△ABC≌△A′B′C′.‎ ‎[解析]　(1)A中x不确定，x2－1＝0的真假无法判断；B中2＋3＝8是命题，且是假命题；C不是陈述句，故不是命题；D中“大”的标准不确定，无法判断真假．‎ ‎(2)①中x有范围，可以判断真假，因此是命题；②是疑问句，不是命题；③是陈述句，但“大”的标准不确定，无法判断真假，因此不是命题；④是陈述句且能判断真假，因此是命题；⑤是祈使句，不是命题．‎ ‎[答案]　(1)B　(2)①④‎ ‎[规律方法]　判断一个语句是否是命题的二个关键点 ‎(1)命题是可以判断真假的陈述句，因此，疑问句、祈使句、感叹句等都不是命题.(2)对于含变量的语句，要注意根据变量的取值范围，看能否判断其真假，若能，就是命题；若不能，就不是命题. 提醒：若语句中含有变量，但变量没有给出范围，则该语句不是命题.‎ ‎[跟踪训练]‎ ‎1．判断下列语句是不是命题，并说明理由．‎ ‎(1)函数f(x)＝3x(x∈R)是指数函数；‎ ‎(2)x2－3x＋2＝0；‎ ‎(3)若x∈R，则x2＋4x＋7>0.‎ 6‎ ‎(4)垂直于同一条直线的两条直线一定平行吗？‎ ‎(5)一个数不是奇数就是偶数；‎ ‎(6)‎2030年6月1日上海会下雨．‎ ‎[解]　(1)是命题，满足指数函数的定义，为真命题．‎ ‎(2)不是命题，不能判断真假．‎ ‎(3)是命题．当x∈R时，x2＋4x＋7＝(x＋2)2＋3>0能判断真假．‎ ‎(4)疑问句，不是命题．‎ ‎(5)是命题，能判断真假．‎ ‎(6)不是命题，不能判断真假．‎ 命题的构成 ‎　(1)已知命题：弦的垂直平分线经过圆心并且平分弦所对的弧，若把上述命题改为“若p则q”的形式，则p是________，q是________.‎ ‎ 【导学号：97792001】‎ ‎(2)把下列命题改写成“若p，则q”的形式，并判断命题的真假．‎ ‎①函数y＝lg x是单调函数；‎ ‎②已知x，y为正整数，当y＝x＋1时，y＝3，x＝2；‎ ‎③当abc＝0时，a＝0且b＝0且c＝0.‎ ‎[思路探究]　解决此类题目的关键是找到命题的条件和结论，然后用适当的形式改写成“若p，则q的形式”．‎ ‎[解析]　(1)命题的条件是“弦的垂直平分线”，结论是“经过圆心并且平分弦所对的弧”．因此p是“一条直线是弦的垂直平分线”，q是“这条直线经过圆心并且平分弦所对的弧”．‎ ‎[答案]　一条直线是弦的垂直平分线　这条直线经过圆心且平分弦所对的弧．‎ ‎(2)①若函数是对数函数y＝lg x，则这个函数是单调函数．‎ ‎②已知x，y为正整数，若y＝x＋1，则y＝3，x＝2.‎ ‎③若abc＝0，则a＝0且b＝0且c＝0.‎ ‎[规律方法]　1.若一个命题有大前提，则在将其改写成“若p，则q”的形式时，大前提仍应作为大前提，不能写在条件中，如本例(2)②.‎ ‎2．“若p，则q”这种形式是数学中命题的基本结构形式，也有一些命题的叙述比较简洁，并不是以“若p，则q”这种形式给出的，这时，首先要把这个命题补充完整，然后确定命题的条件和结论．‎ ‎[跟踪训练]‎ ‎2．把下列命题改写成“若p，则q”的形式．‎ 6‎ ‎(1)当>时，a，则ab，则‎2a>2b；‎ ‎②命题“若a，b是无理数，则a＋b是无理数”是真命题；‎ ‎③直线x＝是函数y＝sin x的一条对称轴；‎ ‎④在△ABC中，若·>0，则△ABC是钝角三角形．‎ 其中为真命题的是________．‎ ‎[思路探究]　 ‎[解析]　对于①，根据函数f(x)＝2x的单调性知①为真命题．‎ 对于②，若a＝1＋，b＝1－，则a＋b＝2不是无理数，因此②是假命题．‎ 对于③，函数y＝sin x的对称轴方程为x＝＋kπ，k∈Z，故③为真命题．‎ 对于④，因为·＝||||cos(π－B)＝－||||cosB>0，故得cosB<0，从而得B为钝角，所以④为真命题．‎ ‎[答案]　①③④‎ 母题探究：1.(变结论)本例中命题①变为“若a>b，则方程ax2－2bx＋a＝0无实根”，该命题是真命题还是假命题．‎ ‎[解]　若a＝1，b＝－5，满足a>b，但Δ＝4b2－‎4a2‎ 6‎ ‎>0，方程有两个不相等的实根，因此该命题是假命题．‎ ‎2．(变条件)本例中命题④变为“若·<0，则△ABC是锐角三角形”，该命题还是真命题吗？‎ ‎[解]　不是真命题，·<0只能说明∠B是锐角，其他两角的情况不确定．只有三个角都是锐角，才可以判定三角形为锐角三角形．‎ ‎[规律方法]　1.由命题的概念可知，一个命题要么是真的，要么是假的，且必居其一．‎ ‎2．如果要判断一个命题为真命题，需要依据条件进行严格的推理论证，而要判断一个命题为假命题，只要举出一个反例即可．‎ ‎[当 堂 达 标·固 双 基]‎ ‎1．下列语句不是命题的个数为(　　)‎ ‎①2<1；②x<1；③若x<1，则x<2；④函数f(x)＝x2是R上的偶函数．‎ A．0　　　B．‎1　‎　　　C．2　　　D．3‎ B　[语句①、③、④都能判断真假，是命题，语句②不能判断真假，不是命题．]‎ ‎2．命题“平行四边形的对角线既互相平分，也互相垂直”的结论是(　　)‎ A．这个四边形的对角线互相平分 B．这个四边形的对角线互相垂直 C．这个四边形的对角线既互相平分，也互相垂直 D．这个四边形是平行四边形 C　[把命题改写成“若p，则q”的形式后可知C正确．故选C.]‎ ‎3．下列命题是真命题的为(　　) ‎ ‎【导学号：97792002】‎ A．若a>b，则< B．若b2＝ac，则a，b，c成等比数列 C．若|x|，故A是假命题．‎ 对于B，当a＝b＝0时，满足b2＝ac，但a，b，c不是等比数列，故B是假命题．‎ 对于C，因为y>|x|≥0，则x2