2020高中数学 第3章 不等式组与简单的线性规划问题2 不等式组表示的平面区域学案 苏教版必修5 4页

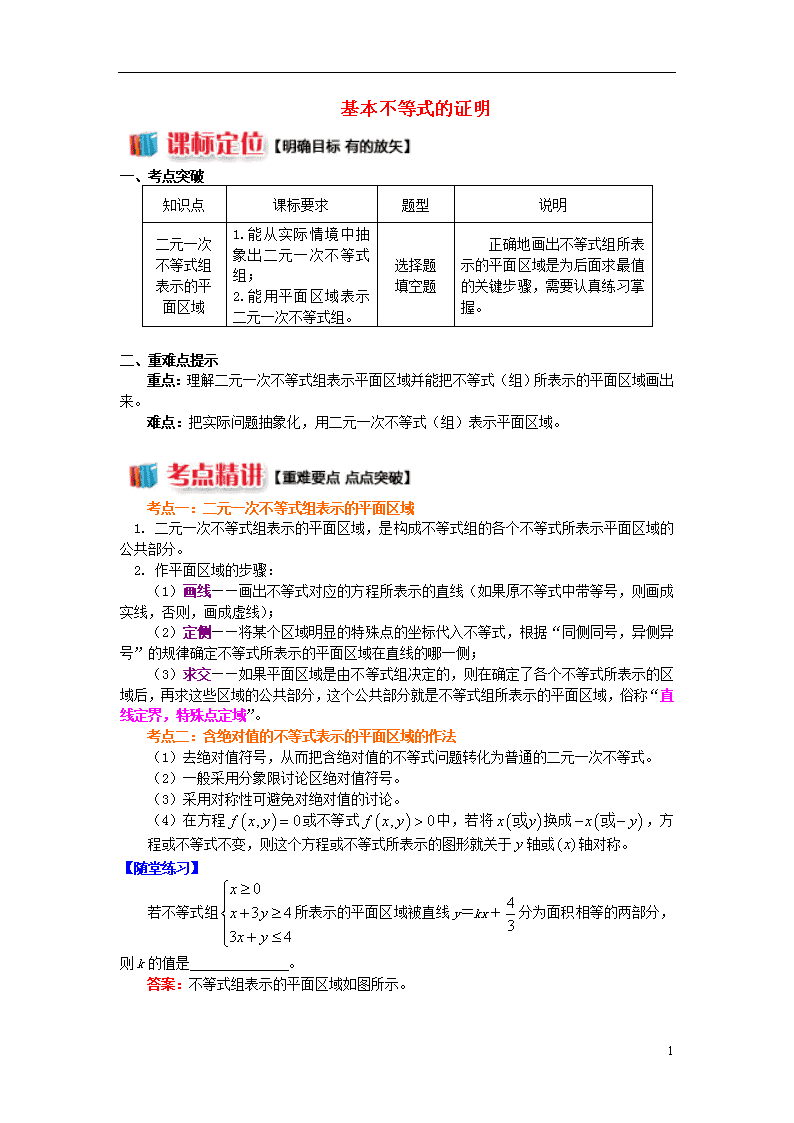
基本不等式的证明 一、考点突破 知识点 课标要求 题型 说明 二元一次不等式组表示的平面区域 ‎1.能从实际情境中抽象出二元一次不等式组；‎ ‎2.能用平面区域表示二元一次不等式组。‎ 选择题 填空题 正确地画出不等式组所表示的平面区域是为后面求最值的关键步骤，需要认真练习掌握。‎ 二、重难点提示 重点：理解二元一次不等式组表示平面区域并能把不等式（组）所表示的平面区域画出来。‎ 难点：把实际问题抽象化，用二元一次不等式（组）表示平面区域。‎ 考点一：二元一次不等式组表示的平面区域 ‎1. 二元一次不等式组表示的平面区域，是构成不等式组的各个不等式所表示平面区域的公共部分。‎ ‎2. 作平面区域的步骤：‎ ‎（1）画线——画出不等式对应的方程所表示的直线（如果原不等式中带等号，则画成实线，否则，画成虚线）；‎ ‎（2）定侧——将某个区域明显的特殊点的坐标代入不等式，根据“同侧同号，异侧异号”的规律确定不等式所表示的平面区域在直线的哪一侧；‎ ‎（3）求交——如果平面区域是由不等式组决定的，则在确定了各个不等式所表示的区域后，再求这些区域的公共部分，这个公共部分就是不等式组所表示的平面区域，俗称“直线定界，特殊点定域”。‎ 考点二：含绝对值的不等式表示的平面区域的作法 ‎（1）去绝对值符号，从而把含绝对值的不等式问题转化为普通的二元一次不等式。‎ ‎（2）一般采用分象限讨论区绝对值符号。‎ ‎（3）采用对称性可避免对绝对值的讨论。‎ ‎（4）在方程或不等式中，若将换成，方程或不等式不变，则这个方程或不等式所表示的图形就关于轴或轴对称。‎ ‎【随堂练习】‎ 若不等式组所表示的平面区域被直线y＝kx＋分为面积相等的两部分，则k的值是 。 ‎ 答案：不等式组表示的平面区域如图所示。‎ 4‎ 由于直线y＝kx＋过定点，因此只有直线过AB中点时，直线y＝kx＋能平分平面区域。‎ 因为A（1，1），B（0，4），所以AB中点D。‎ 当y＝kx＋过点时，＋，‎ 所以k＝。‎ 思路分析：画出平面区域，显然点在已知的平面区域内，直线过定点，结合图形寻找直线平分平面区域面积的条件即可。‎ 技巧点拨：不等式组表示的平面区域是各个不等式所表示的平面区域点集的交集，画出图形后，面积关系可结合平面知识探求。‎ 例题1 （画二元一次不等式组表示的平面区域）‎ 画出不等式组表示的平面区域。‎ 思路分析：分别画出三个不等式表示的区域→找出公共区域。‎ 答案：原不等式组等价于 将（1，0）分别代入①②③的左边知不等式①表示的平面区域在直线x－y＝0的下方；‎ 不等式②表示的平面区域在直线x＋2y－4＝0的下方；‎ 不等式③表示的平面区域在直线y＋2＝0的上方。‎ 故不等式组表示的平面区域为图所示中的三角形阴影部分。‎ 4‎ 技巧点拨：‎ ‎1. 本例中，应先对每一个不等式所表示的平面区域作出正确的判断，保证不因某一个不等式所表示的平面区域产生错误，其次应注意不等式所表示的平面区域是否包括边界。‎ ‎2. 画二元一次不等式组表示的平面区域的步骤：画线→定侧→求“交”→表示。‎ 例题2 （由平面区域求二元一次不等式组）‎ 已知点A（3，－1），点B（－1，1），点C（1，3），写出△ABC的内部区域所对应的二元一次不等式组。‎ ‎ 思路分析：先求出边界所在直线的方程，再根据区域与边界的位置关系确定不等号是“＞”还是“＜”。‎ 答案：‎ 如图所示，直线AB的方程为，即x＋2y－1＝0，区域在直线AB的上方，故x＋2y－1＞0。‎ 直线AC的方程为，即2x＋y－5＝0，‎ 区域在直线AC的下方，故2x＋y－5＜0。‎ 直线BC的方程为，即x－y＋2＝0，‎ 区域在直线BC的下方，故x－y＋2＞0。‎ 所以△ABC的内部区域所对应的二元一次不等式组为。‎ 技巧点拨：‎ ‎1. 本例中，要求写出的是△ABC的“内部区域”所对应的二元一次不等式组，不包括边界，故不等式组中的各个不等式均不带等号。‎ ‎2. 由平面区域求不等式组的步骤：‎ ‎（1）在平面区域内取一点P（x0，y0）；‎ ‎（2）设一边界所在直线方程为Ax＋By＋C＝0，得P（x0，y0），代入到Ax＋By＋C中，比较Ax0＋By0＋C与0的关系，确定不等号；‎ ‎（3）依次同理确定其他不等式；‎ ‎（4）得不等式组。‎ ‎ ‎ 由不等式组画平面区域时忽视不等式的符号致误 4‎ ‎【例析】画出不等式组表示的平面区域。 ‎ ‎【错解】先画直线x－y－1＝0和直线2x－y－3＝0，x－y－1＜0表示直线x－y－1＝0及其下方的平面区域，2x－y－3≥0表示直线2x－y－3＝0及其上方的平面区域，所以不等式组表示的平面区域如图所示。‎ ‎【错因分析】本题的错解中误认为Ax＋By＋C＜0表示的平面区域一定在直线Ax＋By＋C＝0的下方，Ax＋By＋C＞0表示的平面区域一定在直线Ax＋By＋C＝0的上方，而且虚、实线弄错。‎ ‎【防范措施】在解决此类问题时，要严格按照步骤去做，不要想当然。‎ ‎【正解】先画直线x－y－1＝0（虚线），不等式x－y－1＜0表示直线x－y－1＝0及其上方的平面区域。画出直线2x－y－3＝0（实线），不等式2x－y－3≥0表示直线2x－y－3＝0及其下方的平面区域。所以不等式组表示的平面区域如图所示。‎ 4‎