2020高中数学 第一章 三角函数 4页

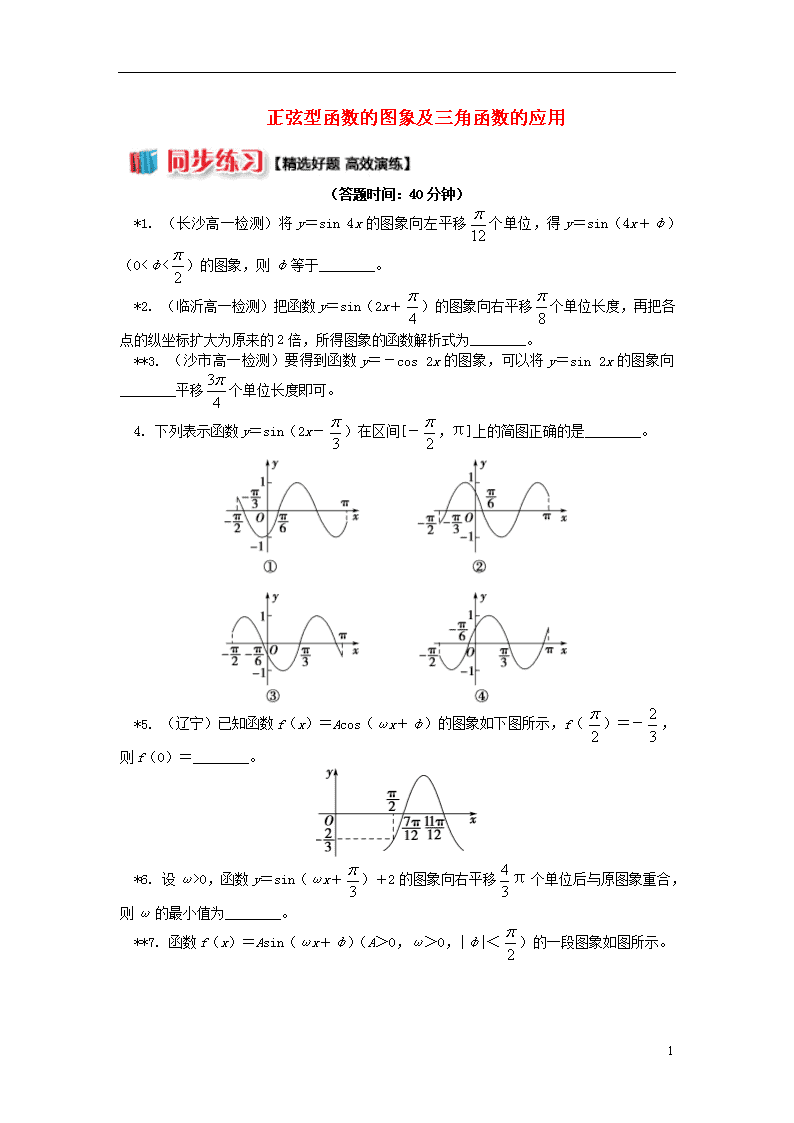
正弦型函数的图象及三角函数的应用 ‎（答题时间：40分钟）‎ ‎*1. （长沙高一检测）将y＝sin 4x的图象向左平移个单位，得y＝sin（4x＋φ）（0<φ<）的图象，则φ等于________。‎ ‎*2. （临沂高一检测）把函数y＝sin（2x＋）的图象向右平移个单位长度，再把各点的纵坐标扩大为原来的2倍，所得图象的函数解析式为________。‎ ‎**3. （沙市高一检测）要得到函数y＝－cos 2x的图象，可以将y＝sin 2x的图象向________平移个单位长度即可。‎ ‎4. 下列表示函数y＝sin（2x－）在区间[－，π]上的简图正确的是________。‎ ‎*5. （辽宁）已知函数f（x）＝Acos（ωx＋φ）的图象如下图所示，f（）＝－，则f（0）＝________。‎ ‎*6. 设ω>0，函数y＝sin（ωx＋）＋2的图象向右平移π个单位后与原图象重合，则ω的最小值为________。‎ ‎**7. 函数f（x）＝Asin（ωx＋φ）（A＞0，ω＞0，|φ|＜）的一段图象如图所示。‎ 4‎ ‎（1）求f（x）的解析式；‎ ‎（2）把f（x）的图象向左至少平移多少个单位，才能使得到的图象对应的函数为偶函数？‎ ‎**8. （济南高一检测）已知曲线y＝Asin（ωx＋φ）（A＞0，ω＞0）上的一个最高点的坐标为（，），此点到相邻最低点间的曲线与x轴交于点（π，0）（如图），若φ∈（－，），‎ ‎（1）试求这条曲线的函数表达式；‎ ‎（2）用“五点法”画出（1）中函数在[0，π]上的图象。‎ 4‎ ‎1. 解析：将y＝sin 4x的图象向左平移个单位得到函数y＝sin 4（x＋）＝sin（4x＋），由sin（4x＋φ）＝sin（4x＋）及0＜φ＜，知φ＝。‎ ‎2. y＝2sin 2x 解析：将函数y＝sin（2x＋）图象右移个单位得函数y＝sin[2（x－）＋]的图象，再将纵坐标伸长到原来的2倍得到函数y＝2sin 2x的图象。‎ ‎3. 左 解析：y＝－cos 2x＝sin（2x＋）＝sin[2（x＋）]，所以将y＝sin 2x的图象向左平移个单位长度即可。‎ ‎4. ① 解析：将y＝sin x的图象上所有点的横坐标缩短为原来的倍，再将所有点向右平移个单位长度即得y＝sin（2x－）的图象，依据此变换过程可得到①中图象是正确的。也可以分别令2x－＝0，，π，，2π得到五个关键点，描点连线即得函数y＝sin（2x－）的图象。‎ ‎5. 解析：由图象可得最小正周期为π，于是f（0）＝f（），注意到π与关于对称，所以f（）＝－f（）＝。‎ ‎6. 解析：由题意知是函数周期的整数倍，又ω>0，‎ ‎∴·k＝，∴ω＝k（k∈Z），∴ω的最小值为。‎ ‎7. （1）f（x）＝3sin（x－） （2）‎ 解析：（1）A＝3，＝×（4π－）＝5π，故ω＝。‎ 由f（x）＝3sin（x＋φ）过点（，0），得sin（＋φ）＝0，又|φ|＜，故φ＝－，∴f（x）＝3sin（x－）。‎ ‎（2）由f（x＋m）＝3sin[（x＋m）－]＝3sin（x＋－）为偶函数（m＞0），知－＝kπ＋（k∈Z），即m＝kπ＋（k∈Z），∵m＞0，∴mmin＝。‎ 4‎ 故至少把f（x）的图象向左平移个单位长度，才能使得到的图象对应的函数是偶函数。‎ ‎8. （1） y＝sin（2x＋） （2）见解析 解析：（1）∵曲线上的一个最高点的坐标为（，），‎ ‎∴A＝，‎ 又此点到相邻最低点间的曲线与x轴交于点（，0），‎ ‎∴＝－，即T＝π，∴ω＝＝2。‎ 取点（，）作为“五点法”中函数的第二个点，‎ ‎∴2×＋φ＝，∴φ＝，‎ 且∈（－，）。‎ 故这条曲线的函数表达式为：‎ y＝sin（2x＋）。‎ ‎（2）列出x，y的对应值表：‎ x ‎－‎ π π π ‎2x＋‎ ‎0‎ π π ‎2π y ‎0‎ ‎0‎ ‎0‎ 作图如下：‎ 4‎