2020学年高一数学下学期期末考试试题 理人教版 13页

- 1 - 2019 学年高一数学下学期期末考试试题 理 I 卷（总分 60 分） 一、选择题(共 12 小题，每小题 5 分，每小题都只有一个正确选项) 1．已知集合 A={x|﹣2＜x＜4}，B={x|y=lg（x﹣2）}，则 A∩（CRB）=（ ） A．（2，4） B．（﹣2，4） C．（﹣2，2） D．（﹣2，2] 2．已知直线 3x+4y+3=0 与直线 6x+my﹣14=0 平行，则它们之间的距离是（ ） A．2 B．8 C． D． 3．函数 f（x）= xe ﹣x 的零点所在的区间是（ ） A．（﹣1， 2 1 ） B．（ 2 1 ，0） C．（0， ） D．（ ，1） 4．设 3 1loga 2 1 ，b= 2 1 2 1      ，c= 3 1 3 1      ，则 a，b，c 的大小关系是（ ） A．a＜b＜c B．c＜b＜a C．b＜c＜a D．c＜a＜b 5．圆锥的表面积是底面积的 3 倍，那么该圆锥的侧面展开图的圆心角为（ ） A．120° B．150° C．180° D．240° 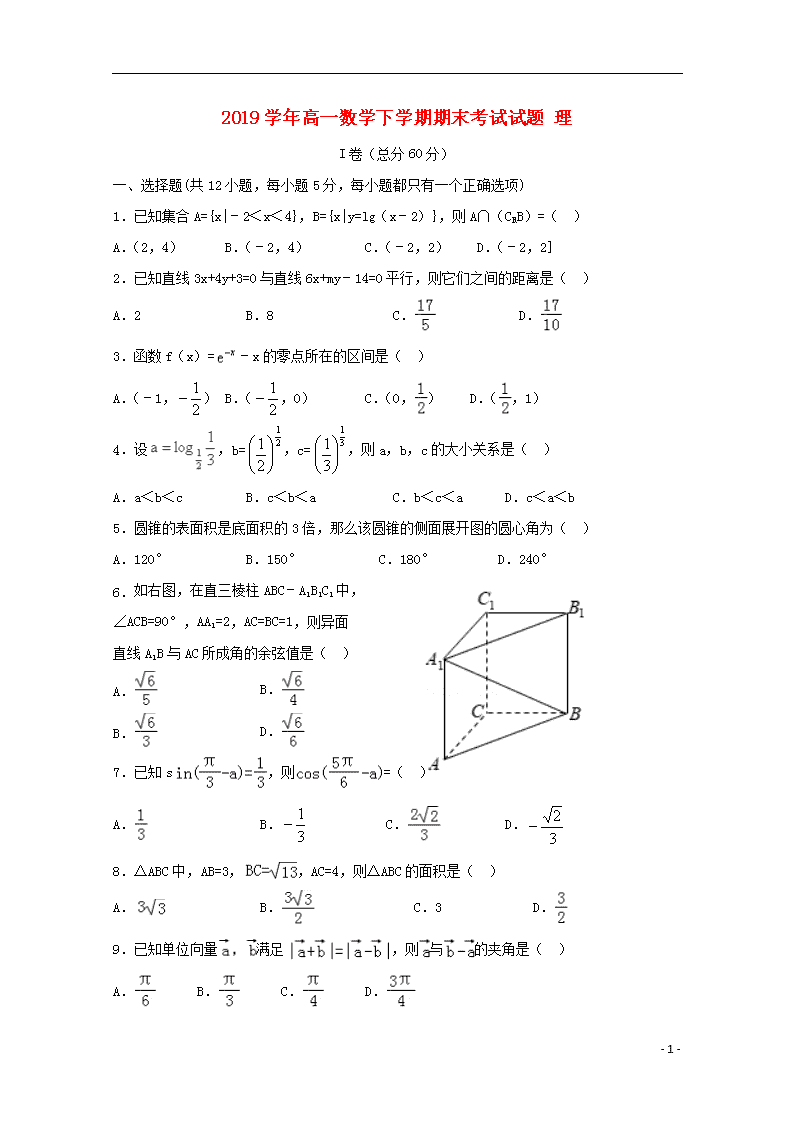6．如右图，在直三棱柱 ABC﹣A1B1C1 中， ∠ACB=90°，AA1=2，AC=BC=1，则异面 直线 A1B 与 AC 所成角的余弦值是（ ） A． B． B． D． 7．已知 s ，则 =（ ） A． B． 3 1 C． D． 3 2 8．△ABC 中，AB=3， ，AC=4，则△ABC 的面积是（ ） A． B． C．3 D． 9．已知单位向量 满足 ，则 与 的夹角是（ ） A． B． C． D． - 2 - 10．已知四棱锥 P﹣ABCD 的三视图如图所示， 则该四棱锥的五个面中的最大面积是（ ） A．3 B．6 C．8 D．10 11．已知图①中的图象对应的函数 y=f（x），则图②中的图象对应的函数是（ ） A．y=f（|x|） B．y=|f（x）| C．y=f（﹣|x|） D．y=﹣f（|x|） 12．已知函数 f（x）是定义域为 R 的周期为 3 的奇函数，且当 x∈（0，1.5）时 f（x）=ln （x2﹣x+1），则方程 f（x）=0 在区间[0，6]上的解的个数是（ ） A．3 B．5 C．7 D．9 II 卷（总分 90 分） 二、填空题(共 4 小题，每小题 5 分) 13．在等差数列{an}中，a2=3，a1+a7＞10，则公差 d 的取值范围是 ． 14．已知角α的终边经过点 P（4a，3a）（a＜0），则 25sinα﹣7tan2α的值为 ． 15．函数 为 R 上的单调函数，则实数 a 的取值范围是 ． 16．如图，矩形 ABCD 中，AB=2AD，E 为边 AB 的中点，将△ADE 沿直线 DE 翻折成△A1DE（A1∉ 平面 ABCD），若 M 为线段 A1C 的中点，则在△ADE 翻折过程中，下列结论正确的是 ．（写 出所有正确结论的序号） ①V ：V =1：3； ②存在某个位置，使 DE⊥A1C； ③总有 BM∥平面 A1DE； ④线段 BM 的长为定值． 三、解答题(共 6 小题，除 17 题 10 分外，其余每题 12 分) 17．已知点 A（0，2），B（4，4）， ； - 3 - （1）若 t1=4cosθ，t2=sinθ，θ∈R，求 在 方向上投影的取值范围； （2）若 t1=a2，求当 ，且△ABM 的面积为 12 时，a 和 t2 的值． 18．已知正数等比数列{an}的前 n 项和 Sn 满足： ． （1）求数列{an}的首项 a1 和公比 q； （2）若 bn=nan，求数列{bn}的前 n 项和 Tn． 19．如右图，在△ABC 中，角 A，B，C 所对的边 分别为 a，b，c，若 2acosA=bcosC+ccosB． （1）求角 A 的大小； （2）若点 D 在边 AC 上，且 BD 是∠ABC 的平分线，AB=2，BC=4，求 AD 的长． 20．函数 f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ ）的部分图象如图所示． （1）求 f（x）的解析式； （2）将 y=f（x）图象上所有点向左平行移动 个 单位长度，得到 y=g（x）图象，求函数 y=g（x）在 [0，π]上的单调递增区间． 21．已知直线 l：（2m+1）x+（m+1）y﹣7m﹣4=0，m∈R，圆 C：（x﹣1）2+（y﹣2）2=25． （1）证明：直线 l 恒过一定点 P； （2）证明：直线 l 与圆 C 相交； （3）当直线 l 被圆 C 截得的弦长最短时，求 m 的值． 22．如图，已知菱形 AECD 的对角线 AC，DE 交于点 F，点 E 为的 AB 中点．将三角形 ADE 沿线 段 DE 折起到 PDE 的位置，如图 2 所示． - 4 - （1）求证：DE⊥平面 PCF； （2）证明：平面 PBC⊥平面 PCF； （3）在线段 PD，BC 上是否分别存在点 M，N，使得平面 CFM∥平面 PEN？若存在，请指出点 M， N 的位置，并证明；若不存在，请说明理由． - 5 - 参考答案与试题解析 一、选择题(共 12 小题) 1．【解答】解：B={x|x＞2}； ∴∁ RB={x|x≤2}； ∴A∩（∁ RB）=（﹣2，2]． 故选：D． 2．【解答】解：直线 3x+4y+3=0 与直线 6x+my﹣14=0 平行， ∴ ≠ ， 解得 m=8． 直线 6x+my﹣14=0，即直线 6x+8y﹣14=0，化为 3x+4y﹣7=0， ∴它们之间的距离= =2． 故选：A． 3．【解答】解：∵函数 f（x）=e﹣x﹣x，画出 y=e﹣x 与 y=x 的图象，如下图： ∵当 x= 时，y= ＞ ， 当 x=1 时，y= ＜1， ∴函数 f（x）=e﹣x﹣x 的零点所在的区间是（ ，1）． 故选：D． 4．【解答】解：a=log =log23＞1，1＞b=（ ） = ＞c=（ ） = ， - 6 - 则 c＜b＜a， 故选：B． 5．【解答】解：设圆锥底面半径为 r，母线长为 l， 侧面展开图扇形的圆心角为θ， 根据条件得：πrl+πr2=3πr2，即 l=2r， 根据扇形面积公式得： =πrl，即 = =180°． 故选：C． 6．【解答】解：连结 BC1，∵AC∥A1C1， ∴∠C1A1B 是异面直线 A1B 与 AC 所成角（或所成角的补角）， ∵在直三棱柱 ABC﹣A1B1C1 中，∠ACB=90°，AA1=2，AC=BC=1， ∴AB= ， ，BC1= = ，A1C1=1， ∴cos∠C1A1B= = = ， ∴异面直线 A1B 与 AC 所成角的余弦值为 ． 故选：D． 7．【解答】解：∵s ， ∴ =cos[ +（ ）] =﹣sin（ ）=﹣ ． 故选：B． 8．【解答】解：根据题意，△ABC 中，AB=3， ，AC=4， 则有 cosC= = = ， - 7 - 则 sinC= ， 则△ABC 的面积 S= |AB||AC|×sinC=3 ， 故选：A． 9. 【解答】解：∵ ， ∴ = ， ∴ • =0， ⊥ ， 如图所示：则 与 的夹角是 ， 故选：D． 10．【解答】解：由三视图知：几何体为四棱锥，且四棱锥的一个侧面与底面垂直， 底面为矩形，矩形的边长分别为 2、4，底面面积=2×4=8； 由正视图可得四棱锥的高为 = ， △SAD 的面积为 ×4× =2 ， 侧面 SAB 与侧面 SCD 为直角三角形，其面积为 3×2× =3， 侧面 SBC 为等腰三角形，底边上的高为 =3， ∴△SBC 的面积为 ×4×3=6． 故选：C． - 8 - 11．【解答】解：设所求函数为 g（x）， g（x）= =f（﹣|x|），C 选项符合题意． 故选：C． 12．【解答】解：∵当 x∈（0，1.5）时 f（x）=ln（x2﹣x+1）， 令 f（x）=0，则 x2﹣x+1=1，解得 x=1 又∵函数 f（x）是定义域为 R 的奇函数， ∴在区间∈[﹣1.5，1.5]上， f（﹣1）=f（1）=0， f（0）=0 f（1.5）=f（﹣1.5+3）=f（﹣1.5）=﹣f（﹣1.5） ∴f（﹣1）=f（1）=f（0）=f（1.5）=f（﹣1.5）=0 又∵函数 f（x）是周期为 3 的周期函数 则方程 f（x）=0 在区间[0，6]上的解有 0，1，1.5，2，3，4，4.5，5，6 共 9 个 故选：D． 二、填空题(共 4 小题) 13．【解答】解：∵a1+a7=2a4=2（a2+2d）=6+4d＞10， ∴d＞1， 故答案为：（1，+∞） 14．【解答】解：∵角α的终边经过点 P（4a，3a）（a＜0）， ∴x=4a，y=3a， ， ∴ ， ， - 9 - ∴ ， ∴ ． 故答案为：﹣39． 15．【解答】解：①若 f（x）在 R 上单调递增， 则有 ，解得 2＜a≤3； ②若 f（x）在 R 上单调递减， 则有 ，a 无解， 综上所述，得实数 a 的取值范围是（2，3]． 故答案为：（2，3] 16.【解答】解：在①中，设 A1 到平面 EBCD 的距离为 h，Dgc AB 的距离为 h′， 则 V ：V = ： =S△ADE：S 梯形 EBCD= ： ′=1：3， 故①正确； 在②中，A1C 在平面 ABCD 中的射影为 AC，AC 与 DE 不垂直， ∴DE 与 A1C 不垂直，故②错误； 在③中，取 CD 中点 F，连接 MF，BF，则 MF∥A1D 且 MF= A1D，FB∥ED 且 FB=ED， 由 MF∥A1D 与 FB∥ED，可得平面 MBF∥平面 A1DE，∴总有 BM∥平面 A1DE，故③正确； ∴∠MFB=∠A1DE，由余弦定理可得 MB2=MF2+FB2﹣2MF•FB•cos∠MFB 是定值，故④正确． 故答案为：①③④． - 10 - 四、解答题(共 9 小题) 17.【解答】（1） ， ， ∴ 在 方向上投影为| |•cos＜ ， ＞= = =4 t2+ t1=4 （sinθ+cosθ）=8sin（θ+ ）； ∴ 在 方向上投影的范围为[﹣8，8]； （2） ， ，且 ， ∴ ， ； ∴点 M 到直线 AB：x﹣y+2=0 的距离为： ； ∴ ， 解得 a=±2，t2=﹣1． 18．【解答】解：（1）∵ ，可知 ， ， 两式相减得： ，∴ ，而 q＞0，则 ． 又由 ，可知： ， ∴ ， ∴a1=1． （2）由（1）知 ． ∵ ， ∴ ， ． 两式相减得 = ． ∴ ． 19．【解答】解：（1）∵2acosA=bcosC+ccosB， - 11 - ∴2sinAcosA=sinBcosC+sinCcosB=sin（B+C）=sinA， ∵sinA≠0，∴cosA= ， ∴A= ． （2）在△ABC 中，由余弦定理的 cosA= = ， 解得 AC=1+ 或 AC=1﹣ （舍）． ∵BD 是∠ABC 的平分线， ∴ = ， ∴AD= AC= ． 20．【解答】 解：（1）由图象可知，A=2，周期 T= [ ﹣（﹣ ）]=π， ∴ =π，ω＞0，则ω=2，…（3 分） 从而 f（x）=2sin（2x+φ），代入点（ ，2）， 得 sin（ +φ）=1，则 +φ= +2kπ，k∈Z，即φ=﹣ +2kπ，k∈Z， 又|φ|＜ ，则φ=﹣ ， ∴f（x）=2sin（2x﹣ ），…（6 分） （2）由（1）知 f（x）=2sin（2x﹣ ）， 因此 g（x）=2sin[2（x+ ）﹣ ]=2sin（2x﹣ ），…（8 分） 令 2kπ﹣ ≤2x﹣ ≤2kπ+ ，k∈Z，可得：kπ﹣ ≤x≤kπ+ ，k∈Z，…（10 分） ， 故函数 y=g（x）在[0，π]上的单调递增区间为[0， ]，[ ，π]．…（12 分） 21.【解答】 证明：（Ⅰ）直线 l 方程变形为（2x+y﹣7）m+（x+y﹣4）=0， 由 ，得 ， - 12 - ∴直线 l 恒过定点 P（3，1）． …（4 分） （Ⅱ）∵P（3，1），圆 C：（x﹣1）2+（y﹣2）2=25 的圆心 C（1，2），半径 r=5， ∴ ， ∴P 点在圆 C 内部， ∴直线 l 与圆 C 相交．…（8 分） 解：（Ⅲ）当 l⊥PC 时，所截得的弦长最短，此时有 kl•kPC=﹣1， 而 ，kPC=﹣ ， ∴ =﹣1，解得 m=﹣ ．…（12 分） 22.【解答】 证明：（Ⅰ）折叠前，因为四边形 AECD 为菱形，所以 AC⊥DE； 所以折叠后，DE⊥PF，DE⊥CF， 又 PF∩CF=F，PF，CF⊂平面 PCF， 所以 DE⊥平面 PCF…………………（4 分） （Ⅱ）因为四边形 AECD 为菱形， 所以 DC∥AE，DC=AE． 又点 E 为 AB 的中点，所以 DC∥EB，DC=EB． 所以四边形 DEBC 为平行四边形．所以 CB∥DE． 又由（Ⅰ）得，DE⊥平面 PCF，所以 CB⊥平面 PCF． 因为 CB⊂平面 PBC， 所以平面 PBC⊥平面 PCF．…………………（9 分） 解：（Ⅲ）存在满足条件的点 M，N，且 M，N 分别是 PD 和 BC 的中点． 如图，分别取 PD 和 BC 的中点 M，N． 连接 EN，PN，MF，CM． 因为四边形 DEBC 为平行四边形， 所以 ． 所以四边形 ENCF 为平行四边形．所以 FC∥EN． 在△PDE 中，M，F 分别为 PD，DE 中点， 所以 MF∥PE． 又 EN，PE⊂平面 PEN，PE∩EN=E，MF，CF⊂平面 CFM， - 13 - 所以平面 CFM∥平面 PEN．…………………（14 分）