浙江省十校联盟2020届高三下学期寒假返校考试数学试题 Word版含解析 28页

- 1 - 浙江十校 一、选择题 1.设集合 ， ，则 （ ） A. B. C. D. 【答案】B 【解析】 【分析】 化简集合 或 ，从而求 再求 ． 【详解】解： 或 ， ， ， 则 ， 故选：B． 【点睛】本题考查了集合的交集和补集运算，以及一元二次不等式的解法． 2.已知双曲线的上、下焦点分别为 ， ， 是双曲线上一点且 ，则双曲线的标准方程为（ ） A. B. C. D. 【答案】C 【解析】 【分析】 由双曲线的定义可得实轴长及半焦距，再由 ， ， 之间的关系求出 ，进而求出双曲线的 方程． 【详解】解：由双曲线的定义可得 ， ， 即 ， ， { }2| 3 4 0A x x x= − − > { }| 2 3B x x= − ≤ ≤ ( )R A B = R [ ]1,3− [ ]2,1− [ ]2,4− { | 4A x x= > 1}x < − { | 1 4}R A x x= −   ( ) { | 1 3}R A B x x= −   2{ | 3 4 0} { | 4A x x x x x= − − > = > 1}x < − { | 2 3}B x x= −   { | 1 4}R A x x= −   ( ) { | 1 3}R A B x x= −   ( )1 0, 3F − ( )2 0,3F P 1 2 4PF PF− = 2 2 14 5 x y− = 2 2 15 4 x y− = 2 2 14 5 y x− = 2 2 15 4 y x− = a b c b 3c = 2 4a = 2a = 2 2 2 9 4 5b c a= − = − = - 2 - 且焦点在 轴上， 所以双曲线的方程为： ， 故选：C． 【点睛】本题考查根据双曲线的定义求标准方程，属于基础题． 3.已知两非零复数 ，若 ，则一定成立 是 A. B. C. D. 【答案】D 【解析】 利用排除法： 当 时， ，而 ，选项 A 错误， ，选项 B 错误， 当 时， ，而 ，选项 C 错误， 本题选择 D 选项. 4.已知 ，则“ ”是“ ”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 必要条件 D. 既不充分也不必要条件 【答案】B 【解析】 【分析】 根据绝对值不等式的性质和特殊值法，判断即可． 【详解】解： ， 因为 ， 所以 ， 故后者能推出前者， 反之，比如 ， ，推不出后者， 的 y 2 2 14 5 y x− = 1 2,z z 1 2 Rz z ∈ 1 2 Rz z ∈ 1 2 Rz z ∈ 1 2 Rz z+ ∈ 1 2 Rz z ∈ 1 21 , 1z i z i= + = − 1 2z z R∈ ( )2 1 2 1 2z z i i R= + = ∉ 1 2 1 1 z i i Rz i += = ∉− 1 21 , 2 2z i z i= + = − 1 2z z R∈ 1 2 3z z i R+ = − ∉ ,a b∈R 1a ≤ 1a b b− + ≤ | | | | | |a b b a b b a− + − + = | | | | 1a b b− +  | | 1a  1a = 3b = - 3 - 故为必要不充分条件， 故选：B. 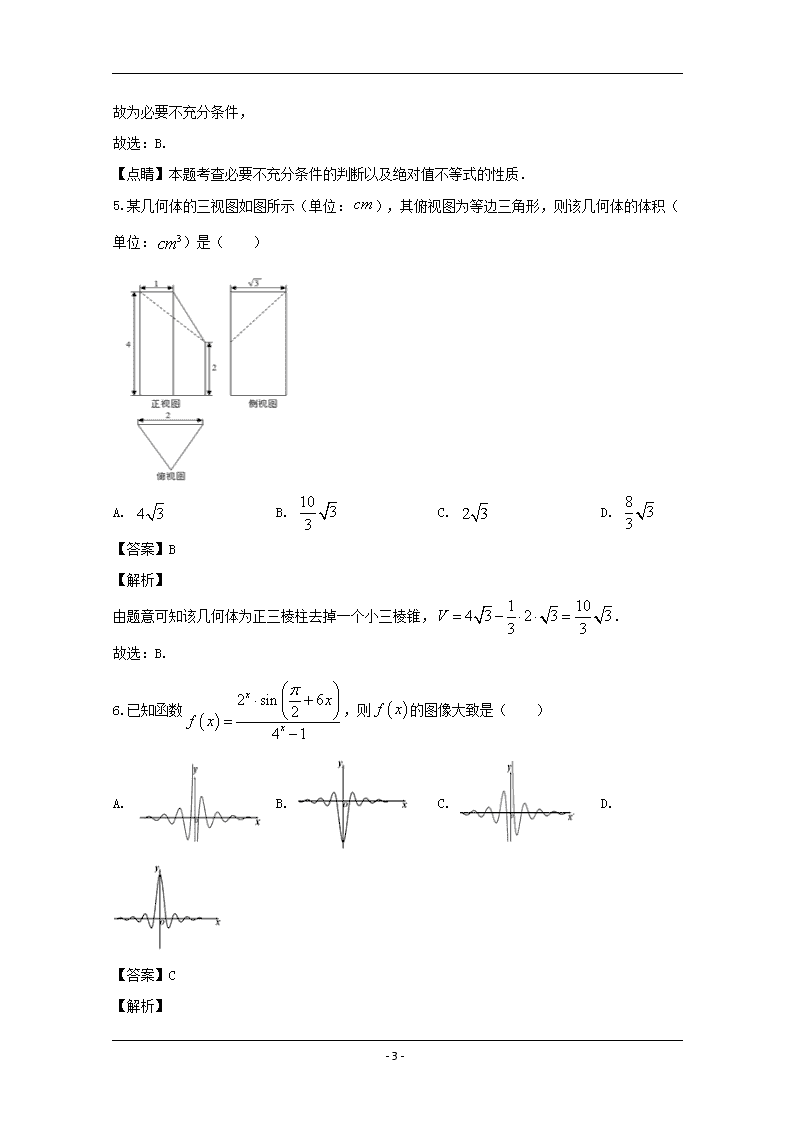【点睛】本题考查必要不充分条件的判断以及绝对值不等式的性质． 5.某几何体的三视图如图所示（单位： ），其俯视图为等边三角形，则该几何体的体积（ 单位： ）是（　　） A. B. C. D. 【答案】B 【解析】 由题意可知该几何体为正三棱柱去掉一个小三棱锥， . 故选：B. 6.已知函数 ，则 的图像大致是（ ） A. B. C. D. 【答案】C 【解析】 cm 3cm 4 3 10 33 2 3 8 33 1 104 3 2 3 33 3V = − ⋅ ⋅ = ( ) 2 sin 62 4 1 x x x f x π ⋅ +  = − ( )f x - 4 - 【分析】 先判断函数的奇偶性，再根据函数值的变化规律，代入特殊值判断，即可得到答案． 【详解】解： 函数 ， ， 为奇函数，故图象关于原点对称，故排除 和 ， ， 可知当 ，即 时， 当 时， 时， ，从左到右 第一个零点为 ， 因为 ，取 ，得 ，则 选项正确. 故选：C. 【点睛】本题考查了函数图象的识别，常用的方法利用函数的奇偶性，单调性，特殊值，零 点等排除. 7.设 ，相互独立的两个随机变量 ， 的分布列如下表： -1 1 -1 1 则当 在 内增大时（ ） A. 减小， 增大 B. 减小， 减小 C. 增大， 增大 D. 增大， 减小 【答案】D 【解析】 【分析】  2 sin( 6 ) 2 cos62( ) 4 1 4 1 x x x x x xf x π + = =− − 2 cos( 6 ) 2 cos6( ) ( )4 1 4 1 x x x x x xf x f x − − −∴ − = = − = −− − ( )f x∴ B D  2 sin( 6 ) 2 cos62( ) 4 1 4 1 x x x x x xf x π + = =− − 6 2x k π π= + 12x k π π= + ( ) 0f x = 0x > 12x π= ( ) 0f x = ( )f x 12 π 0 24 12 π π< < 24x π= ( ) 0f x > C 1 12 p< < ξ η ξ η P 2 3 1 3 P 1 p− p p 1 ,12      ( )E ξ η+ ( )D ξ η+ ( )E ξ η+ ( )D ξ η+ ( )E ξ η+ ( )D ξ η+ ( )E ξ η+ ( )D ξ η+ - 5 - 求出 ， ，从而 ， ， ，从而 ，由此得到当 在 内增大时， 增大， 减小． 【详解】解： ， ， ， ， ， ， ， 当 在 内增大时， 增大， 减小， 故选：D． 【点睛】本题考查离散型随机变量的数学期望、方差的性质等基础知识，考查运算求解能力． 8.如图，矩形 中， ， ， 为 的中点， 沿着 向上翻折， 使点 到 .若 在平面 上的投影 落在梯形 内部（不含边界），设二面角 的大小为 ，直线 ， 与平面 所成角分别为 ， ，则（ ） A. B. C. D. 【答案】C 【解析】 【分析】 1( ) 3E ξ = − ( ) 2 1E pη = − 4( ) 2 3E pξ η+ = − 8( ) 9D ξ = 2( ) 4 4D p pη = − 2 28 1 17( ) 4 4 4( )9 2 9D p p pξ η+ = − + = − − + p 1( ,1)2 ( )E ξ η+ ( )D ξ η+ 1 12 p< < 2 1 1( ) 3 3 3E ξ = − + = − ( ) 1 2 1E p p pη = − + = − 4( ) 2 3E pξ η+ = − 2 21 2 1 1 8( ) ( 1 ) (1 )3 3 3 3 9D ξ = − + × + + × = 2 2 2( ) ( 2 ) (1 ) (2 2 ) 4 4D p p p p p pη = − − + − = − 2 28 1 17( ) 4 4 4( )9 2 9D p p pξ η+ = − + = − − + ∴ p 1( ,1)2 ( )E ξ η+ ( )D ξ η+ ABCD 4AB = 2AD = E CD ADE∆ AE D 'D 'D ABCD H ABCE 'D BC E− − α 'D C 'D B ABC β γ α β γ< < β α γ< < β γ α< < γ β α< < - 6 - 作 出 图 象 ， 根 据 空 间 角 定 义 可 得 ， ， ， 结 合 ，即可得出结论． 【详解】解：由 ， 可知， ，作 中点 ， 则 ， 故 在线段 上， 作 交 于 ，连接 ， ， ，如图， 易知， ， ， ， 又 ， ． 故选：C． 【点睛】本题考查空间角的综合运用，考查逻辑推理能力以及空间想象能力． 9.已知 ，给出下列命题： ①若 ，则 ； ②若 ，则 ； ③若 ，则 ； ④若 ，则 . 其中真命题的个数是（ ） A. 1 B. 2 C. 3 D. 4 【答案】B 【解析】 【分析】 ①若 ，则 ，然后两边平方，再通过作差法即可得解； tan D H HM α ′= tan D H HC β ′= tan D H HB γ ′= HM HB HC< < 2 4AB AD= = DE DA= AB P DP AE⊥ H DP D M BC′ ⊥ BC M HM HB HC tan D H HM α ′= tan D H HC β ′= tan D H HB γ ′= HM HB HC< < β γ α∴ < < 0a b> > 1a b− = 1a b− < 3 3 1a b− = 1a b− < 1a be e− = 1a b− < ln ln 1a b− = 1a b− < 1a b− = 1a b= + - 7 - ②若 ，则 ，然后利用立方差公式可知 ，再结合 以及不等式的性质即可判断； ③若 ，则 ，再利用 ，得出 ，从而求得 的范 围，进而判断； ④取特殊值， ， 即可判断． 【详解】解：①若 ， 则 ， 所以 ， 所以 ，即①错误； 若 ， 则 ， 即 ， 因为 ， 所以 ， 所以 ， 所以 ，即 ，所以②正确； 若 ， 则 ， 因为 ，所以 ， 所以 ，即③正确； ④取 ， ，满足 ， 但 ，所以④错误； 所以真命题有②③， 故选：B． 点睛】本题考查命题真假的判断，涉及根据不等式的性质证明不等式、指对运算法则、立方 差公式等，考查学生的分析能力和运算能力． 【 3 3 1a b− = 3 31a b− = 2 3( 1)( 1)a a a b− + + = 0a b> > 1a be e− = 1 1 1 a b a b b b b e ee e e e − += = = + 0b > 1be > a be − a e= 1b = 1a b− = 1a b= + 1 2a b b= + + 1 2 1a b b− = + > 3 3 1a b− = 3 31a b− = 2 3( 1)( 1)a a a b− + + = 0a b> > 2 2a b> 2 21a a b+ + > 1a b− < 1a b− < 1a be e− = 1 1 1 a b a b b b b e ee e e e − += = = + 0b > 1 2a be e−< < < 1a b− < a e= 1b = 1lna lnb− = 1a b− > - 8 - 10.已知数列 的各项都是正数且满足 ， 是数列 的前 项和，则下列选项中错误的一项是（ ） A. 若 单调递增，则 ； B. 若 ，则 ； C. 若 ，则 D. 若 ，则 . 【答案】D 【解析】 【分析】 由数列递增可得 ，结合数列的递推式，解不等式可判断 ；分别求得 ， ，比较 可判断 ；由数列的递推式可得 ，由累乘法可判断 ；求得 ， ，可判断 ． 【详解】解：数列 的各项都是正数且满足 ， ， 若 单调递增，可得 ， 即为 ， 可得 ， 且 ， 由 ， 可得 ，故 正确； 若 ， 可得 ， 解得 （负值已舍去）， 由 ， ， { }na ( )2 * 12 3 , 2n n na a a n N n−− = ∈ ≥ nS { }na n { }na 10 2a< < 1 1a = 3 4 32 2a< < 1 2a ≠ ( )( ) ( ) ( )1 2 3 22 1 2 1 2 1 22n n aa a a na −+ + + = ≥− 1 3a = ( )3 3 1 4n nS +≥ 1n na a −> A 2a 3a B 1 22 1 2 n n n aa a − −+ = − C 2a 2S D { }na 2 * 12 3 (n n na a a n N−− = ∈ 2)n { }na 1n na a −> 2 1 4 2 0n n n na a a a−− = − > 0 2na< < ( 2n *)n N∈ 1 2a a< 10 2a< < A 1 1a = 2 2 2 12 3 1a a a− = = 2 3 17 4a += 2 3 3 2 3 172 3 4a a a +− = = (*) - 9 - ， 而 在 ， 的范围是 ， ， 而 ， 则 ， ， 故方程 的解在 ， 内，故 正确； 由 ， 可得 ， 即 ， 即 ， 可得 ， 故 正确； 若 ，可得 ， 解得 ， ， 由 ， ， 可得 ，故 错误． 故选：D． 【点睛】本题考查数列的递推公式的运用，考查数列中的项的范围和单调性，以及数列的求 和，考查化简运算能力、推理能力． 二、填空题 11.我国古代数学家赵爽利用“勾股圆方图”巧妙地证明了勾股定理，成就了我国古代数学的 骄傲，后人称之为“赵爽弦图”.如图，它是由四个全等的直角三角形和中间的一个小正方形 拼成的一个大正方形，若直角三角形中较小的锐角记为 ，大正方形的面积为 25，小正方形 的面积为 1，则 ______， ______. 3 17 (1.75,1.8)4 + ∈ 2 2 3 3 3 3 92 3 2( )4 8a a a− = − − 3 4(2 2) 3 4(4 2 3 2− × 2) 3 42 2 2< < 3 44 2 3 2 (4 2 6− × ∈ − 2) (*) 3 4(2 2) B 2 12 3n n na a a −− = 2 12 3 2 2n n na a a −− − = − 1(2 1)( 2) 2n n na a a −+ − = − 1 22 1 2 n n n aa a − −+ = − 11 2 1 2 3 1 2 3 22 2 2(2 1)(2 1) (2 1) ( 2)2 2 2 2 n n n n aa a aa a a aa a a a − −− − −+ + … + = … = ≠− − − − C 1 3a = 2 2 2 12 3 3a a a− = = 2 3 33 4a += 2 3 333 4S += + 3 (3 2 1) 21 4 4 × × + = 3 33 21 33 63 04 4 4 + −+ − = < 2 3 (3 2 1) 4S × × +< D α sinα = sin cos2 2 α α+ = - 10 - 【答案】 (1). (2). 【解析】 【分析】 直接利用三角形的全等，整理出关于一元二次方程，进一步利用关系式的应用求出三角函数 的值． 【详解】解：根据已知条件四个直角三角形全等， 所以设直角三角形的短的直角边长为 ， 则较长的直角边长为 ， 所以 ， 整理得 ， 解得： 或 （负值舍去）， 所以 ． ． 故答案为：① ；② ． 【点睛】本题考查的知识要点：三角函数关系式的变换，二倍角的正弦公式，一元二次方程 的解法和应用，主要考查学生的运算能力和转换能力及思维能力． 12.已知直线 ： 被圆 ： 截得 弦长为 ，则 ______， 圆 上到直线 的的距离为 1 的点有______个. 【答案】 (1). (2). 3 的 3 5 2 10 5 x 1x + 2 2 2( 1) 5x x+ + = 2 12 0x x+ − = 3x = 4− 3sin 5 α = 2 3 2 10sin cos (sin cos ) 1 sin 12 2 2 2 5 5 α α α α α+ = + = + = + = 3 5 2 10 5 l y kx= C ( ) ( )2 21 2 4x y− + + = 2 3 k = C l 3 4 − - 11 - 【解析】 【分析】 利用点到直线的距离公式求出圆心到直线 的距离 ，再根据弦长公式求出 ，解方程求得 值， 【详解】解：由题意得：圆心 ， 则圆心到直线 的距离 ， 解得 ； 因为 ， ， 则圆 上到直线 的距离为 1 的点应有 3 个. 故答案为： ；3． 【点睛】本题考查直线与圆的位置关系，涉及点到直线的距离公式的应用. 13.（1）若二项式 的展开式中存在常数项，则 的最小值为______； （2）从 6 名志愿者中选出 4 人，分别参加两项公益活动，每项活动至少 1 人，则不同安排方 案的种数为____.（用数字作答） 【答案】 (1). 3 (2). 210 【解析】 【分析】 （1）根据二项式展开式的通项公式，令 的指数等于 0，求出 、 的关系，即可求出 的最 小值； （2）根据题意，分 2 步进行分析：①，从 6 名志愿者中选出 4 人，②，将选出的 4 人分成 2 组，分别参加两项公益活动，由分步计数原理计算可得答案. 【详解】解：（1） 的展开式中通项公式为： ， 令 ， 1l d d k (1, 2)C − l 2 2 | 2 | 4 ( 3) 1 kd k += = − + 3 4k = − 1d = 2r = C l 3 4 − ( )*2 n x n N x  − ∈   n x n r n *2( ) ( )nx n N x − ∈ 3 2 1 2( ) ( 2) n rr n r r r r r n nT x x x −− + = − = −    3 02n r− = - 12 - 解得 ， 其中 ，1，2， ， ， 当 时， ， 所以 的最小值为 3． （2）根据题意，分 2 步进行分析： ①从 6 名志愿者中选出 4 人，有 种选法， ②将选出的 4 人分成 2 组，分别参加两项公益活动，有 种情况， 则有 种不同的安排方案， 故答案为：3，210． 【点睛】本题考查利用二项展开式的通项公式求展开式的特定项问题，以及分步计数原理的 应用，涉及排列、组合公式的应用． 14.如图，在 中，内角 ， ， 的对边分别为 ， ， ，若 ， ， ，则 ______，点 为边 上一点，且 ，则 的面积为______. 【答案】 (1). (2). 10 【解析】 【分析】 由已知结合正弦定理可求 ，然后结合二倍角关系可求 ，结合三角形的面积公式及 等高三角形的面积比可转化为底的比可求． 【详解】解：因为 ， ， ， 由正弦定理可得： ， 所以 ， 则 ； ， 3 2n r= 0r = … n 2r = 3n = n 4 6 15C = 42 2 14− = 15 14 210× = ABC∆ A B C a b c 4 5b = 5c = 2B C= cosC = D BC 6BD = ADC∆ 2 5 5 cosC sin B 4 5b = 5c = 2B C= sin sin b c B C = 4 5 5 4 5 sin 2 sin 2sin cosC C C C = = 2 5cos 5C = 2 5 5 4sin 2sin cos 2 5 5 5B C C= = × × = - 13 - ， 由余弦定理可得： ， 解可得 （舍 或 ， 所以 ， ． 故答案为： ，10． 【点睛】本题考查正弦定理，余弦定理，三角形的面积公式在求解三角形中的应用． 15.已知 是椭圆 ： 的左焦点， ， 是椭圆 上的两个相异动点，若 中 点的横坐标为 1，则 到直线 距离的最小值为______. 【答案】 【解析】 【分析】 分直线 的斜率存在和不存在两种情况讨论，由于同一点对称性设斜率大于 0，与椭圆联立 求出两根之和，再由 的中点的横坐标求出参数之间的关系，由点到直线的距离公式求出 到直线 距离．令参数部分为函数，求导，由函数的单调性求出函数的最大值，进而求出 到直线 的最小值． 【详解】解：由题意的方程可得： ， 若直线 的斜率不存在时， 则由题意可得 的方程为： ， 这时 到直线 的距离为 2， 当直线 的斜率存在且不会为 0 时， 由题意的对称性设 ， 设方程为 ， ， ， ， ， 1 45 6 122 5ABDS∆∴ = × × × = 22 5 80 25cos 5 8 5 aC a + −= = 5a = ) 11a = 6 5 ABD ADC S BD S CD ∆ ∆ = = 5 12 106ADCS∆∴ = × = 2 5 5 F C 2 2 14 3 x y+ = A B C AB F AB 15 2 AB AB F AB F AB ( 1,0)F − AB AB 1x = F AB AB 0k > y kx b= + 1(A x 1)y 2(B x 2 )y - 14 - 联立直线与椭圆的方程可得： ， 整理可得： ， △ ， 即 ， ， ， 因为 中点的横坐标为 1， 所以 ， 即 所以 到直线 的距离 令 ， ， ， 当 ， ， 单调递增， 当 ， ， 单调递减， 所以 时 最大， 且 ， 所以 ， 故答案为： ． 【点睛】本题考查椭圆的性质及直线与椭圆的综合，点到直线的距离公式的应用和利用导数 去研究函数的单调性和最值． 2 23 4 12 0 y kx b x y = +  + − = 2 2 2(3 4 ) 8 4 12 0k x kbx b+ + + − = 2 2 2 264 4 (3 4 )(4 12) 0k b k b= − + − > 2 23 3b k< + 1 2 2 8 3 4 kbx x k + = − + 2 1 2 2 4 12 3 4 bx x k −= + AB 2 8 23 4 kb k − =+ 23 4 4 kb k += − F AB 2 2 2 2 4 2 3 4| || | 3 84 1 1 4 k kb k kkd k k k k +− −− += = = + + + 4 2 4 2 2 2 4 2 4 2 4 2 1 64 48 9 1 64( ) 16 9 1 16 9644 4 4 k k k k k k k k k k k k + + + − + −= = = −+ + +   2 4 2 16 9( ) kg k k k −= + 0k > 4 2 2 3 2 2 4 2 2 4 2 2 16 ( ) (16 9)(4 2 ) 2 (2 3)(8 3)( ) ( ) ( ) k k k k k k k k kg k k k k k + − − + − − +′ = =+ + 60 2k< < ( ) 0g k′ > ( )g k 6 2k > ( ) 0g k′ < ( )g k (0, )∈ +∞ 6( )2g 316 96 2( ) 49 32 4 2 g − = = +  1 1564 4 24 2d = − = < 15 2 - 15 - 16.已知向量 ， 满足 ，且 ，则 的取值范围为______. 【答案】 【解析】 分析】 由 和 ，求得 和 的值，以及 的取值范围，再求 的取值 范围，即可得出 的取值范围． 【详解】解：由 ， 得 ，① 又 ， 得 ，② 由①②得 ， ， 且 ， 即 ， ， ， 所以 ， 所以 ， 所以 的取值范围是 ， ． 故答案为： ， ． 【点睛】本题考查了平面向量的数量积运算问题，也考查了运算求解能力． 17.已知函数 ，若函数 有三个互不相同的零点 0， ， ，其中 ，若对任意的 ，都有 成立，则实数 的最小值为 ______. 【答案】 【 a b 2 1a b+ =  ( ) 1a a b⋅ − =   a b−  13 1 13 1,2 2  − +     | 2 | 1a b+ = ( ) 1a a b− =  2a a b 2b 2( )a b−  | |a b−  | 2 | 1a b+ = 2 24 4 1a a b b+ + =   ( ) 1a a b− =  2 1a a b− =  2 21 (5 )8a b= −  21 ( 3 )8a b b= − −  | | | || |a b a b    2 21 1(3 ) (5 ) | |8 8b b b+ − ×    4 29 34 9 0b b− +   217 4 13 17 4 13 9 9b − +   2 2 2 2 2 2 21 1 9 11( ) 2 (5 ) ( 3 )8 4 8 8a b a a b b b b b b− = − + = − − − − + = +         214 2 13 9 11 14 2 13 4 8 8 4b − ++   | |a b−  13 1[ 2 − 13 1]2 + 13 1[ 2 − 13 1]2 + ( ) ( )3 23 0,f x x x ax a a R= − + < ∈ ( )f x 1t 2t 1 2t t< [ ]1 2,x t t∈ ( ) 14f x a≤ + a 9− - 16 - 【解析】 【分析】 由题意可知， ， 是 的根，且 ， ，从而可知 ， ，然后结合导数可求 ，而原题可转化为 ，代入解不等式可求 ． 【详解】解：因为 ， 由题意可知： ， 是 的根， 则 ， ，△ ， ， ， 当 时， ， 则存在 的极大值点 ， ， 且 ， 由题意， ， 将 代入得 ， 解可得 ． 又因为 ， 结合二次函数的性质可知， ， 得 即 的最小值 ． 故答案为： . 【点睛】本题考查一元二次不等式恒成立问题、利用导数求闭区间上函数的最值、不等式的 解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想、分类讨论思想． 三、解答题 18.已知函数 的图像如图所示. 1t 2t 2 3 0x x a− + = 1 2 3t t+ = 1 2 0t t a= < 0a < 1 20t t< < ( )maxf x ( ) 14maxf x a + 3 2 2( ) 3 ( 3 )f x x x ax x x x a= − + = − + 1t 2t 2 3 0x x a− + = 1 2 3t t+ = 1 2 0t t a= < 9 4 0a= − > 0a∴ < 1 20t t< < 1 20t t< < 2 6( ) 3f x x x a= −′ + ( )f x 1 1(x t∈ 0) 2 1 13 6a x x− = − 3 2 1 1 1 1( ) ( ) 3 14maxf x f x x x ax a= = − + + 2 1 13 6a x x− = − ( )3 1 1 8x − − 11 0x− < 2 1 13 6a x x− = − 0 9a< −  9 0a− < a 9− 9− ( ) ( )sin , 0, 0,0 2f x A x x R A πω ϕ ω ϕ = + ∈ > > < <   - 17 - （1）求函数 的解析式； （2）求函数 的单调递增区间. 【答案】（1） ；（2） ， . 【解析】 【分析】 （1）由图知， ，由 ，可求得 ，由 可求得 ； （2）先化简 ，然后利用三角函数的单调性即可得到结论． 【详解】解：（1）∵ ， ∴ ， ， ， ， ∴ . （2） ， ， ， ∵ ， ， ( )f x ( ) 12 12g x f x f x π π   = − − +       ( ) 2sin 2 6f x x π = +   5,12 12k k π ππ π − +   k Z∈ 2A = T π= ω 2sin(2 0 ) 1ϕ× + = ϕ ( )g x 11 5 2 12 12 T π π= − T π= 2ω = sin 1 252 12 A A ϕ π ϕ π = ⇒ = × + = 6 π=ϕ ( ) 2sin 2 6f x x π = +   2sin 212f x x π − =   2sin 212 3f x x π π   + = +       ( ) 2 sin 2 sin 212 12 3f x f x xg x x π π π      = − − + = − +             2sin 2 3x π = −   2 2 22 3 2k x k π π ππ π− ≤ − ≤ + k Z∈ - 18 - 解得单调递增区间： ， . 【点睛】本题考查三角函数解析式的求解，以及三角函数的化简，三角函数的单调性，综合 考查三角函数的性质． 19.如图，四棱锥 中， 是等边三角形，底面 是直角梯形， ， ， ， ， ， 分别是 ， 的中点. （1）①求证： 平面 ； ②求线段 的长度； （2）若 ，求直线 与平面 所成角的正弦值. 【答案】（1）①详见解析；② ；（2） . 【解析】 【分析】 （1）①通过证明面 面 ，再利用面面平行的性质得证；②由余弦定理求解即可； （2）法一：作出图象，设 到平面 的距离设为 ，利用等体积法求出 ，进而可得直 线 与平面 所成角的正弦值为 ． 法二：利用面面垂直的判定定理可证出平面 平面 ，建立空间直角坐标系，通过 空间向量法，求出直线 与平面 所成角的正弦值. 【详解】解：（1）①证明：取 中点 ， 则 ， ， ∵ ， ， ∴平面 平面 ， 5,12 12k k π ππ π − +   k Z∈ P ABCD− PAB∆ ABCD / /AB CD AB AD⊥ 2AB BC= = 3ABC π∠ = F G PC AD / /FG PAB FG 3PC = FG PBC 7 2 3 3 7 / /GFI PAB G PBC h h FG PBC 3 3 7 h FG = POC ⊥ ABC FG PBC BC I / /GI AB / /FI PB GI FI I= AB BP B= / /GFI PAB - 19 - ∴ 平面 . ②由①可知： ， ， ， 由余弦定理得到： . （2）解法一：∵ ， ， ∴ ， 又 ， ， ∴ 平面 ， ∴平面 平面 ， 延长 到 ，使得 ， 则 面 ， ， ∵ ， ， ∴ ， ∵ 是 的中点， . 到平面 的距离设为 ， 体积法求得： ， / /FG PAB 1FI = 3 2IG = 60FIG PBA∠ = ∠ = ° 9 3 71 2 1 cos604 2 2FG = + − × × × ° = 3PO CO= = 3PC = 120POC∠ = ° EO AB⊥ OC AB⊥ AB ⊥ POC POC ⊥ ABC CO H PH OH⊥ PH ⊥ ABC 3 2PH = 2PB BC= = 3PC = 3 7 4PBCS∆ = G AD 3 3 4GBCS∆ = G PBC h 3 7 3 3 3 4 2 4h× = × - 20 - ∴ ， ∴ . 解法二：∵ ， ， ∴ ， 又 ， ， ∴ 平面 ， ∴平面 平面 ， 以 为坐标原点建立空间坐标系，得到 ， ， ， 延长 到 ，使得 ， 则 面 ， ， 则 ， ， ∴ ，由于 ， ， 则法向量 ， ∴直线 与平面 所成角的正弦值为 . 3 21 14h = 3 3sin 7 h FG θ = = 3PO OC= = 3PC = 120POC∠ = ° EO AB⊥ OC AB⊥ AB ⊥ POC POC ⊥ ABC O ( )1,0,0B ( )0,0, 3C 31, ,02G  −    CO H PH OH⊥ PH ⊥ ABC 3 2PH = 3 30, ,2 2P  −    3 30, ,4 4F       3 31, ,4 4FG  = − −     3 31, ,2 2PB  = −     ( )1, 3,0BC = − ( )3,1, 3v = FG PBC 3 3 7 FG v FG v ⋅ = ⋅     - 21 - 【点睛】本题考查线面平行的判定及性质，考查线面角的求解，同时也考查了线面垂直的判 定以及等体积法的运用，考查逻辑推理能力及运算求解能力． 20.设 是数列 的前 项和，且 是 和 2 的等差中项. （1）求数列 的通项公式； （2）记 . ①求数列 的前 项和 ； ②设 ，求证： 【答案】（1） ；（2）① ；②详见解析. 【解析】 【分析】 （1）由 是 和 2 的等差中项，可得 ，当 时， ，相减可得 ： ， 时，可得 ，利用等比数列的通项公式即可得出． （2）①利用等比数列的求和公式可得： ． ，进而得出 ． ②由①可得： ．利用裂项求和可得 ，再利用数列的单调性即可证明 结论． 【详解】解：（1）∵ 是 和 2 的等差中项， ∴ ①， . nS { }na n na nS { }na ( )( )1 1k k k nb a a a k n++ + + ≤⋅ ≤ { }( )1kb k n≤ ≤ n nT ( )2 * 1 2 2 2 2n n M n NT T T = + + + ∈ 1 3 2 4M≤ < ( )*2n na n N= ∈ ( )24 2 2 3 2 13 n n nT = ⋅ − ⋅ + na nS 2 2n nS a+ = 2n 1 12 2n nS a− −+ = 12n na a −= 1n = 1a 1 1 1( ) 2 (2 2 2 ) 2 4k k k n n k k k k k k nb a a a a + + + += + +…+ = + +……+ = − (1 )k n  nT 1 2 3 1 1( )4 2 1 2 1 n n n nT += −− − M na nS 2 2n nS a+ = - 22 - 当 时， ， 解得 ， 当 ， 时， ② ①-②得 ， ∴ ， ∴ ， ∴数列 是首项为 2，公比为 2 的等比数列， ∴ . （2）①记 ， . 数列 的前 项和： ∴ ， ∴ . ②由①进一步得到： ， ∴ ， ∴ ， ∵ ， ∴ . 1n = 1 12 2S a+ = 1 2a = *n N∈ 2n ≥ ( )1 12 2 2n nS a n− −+ = ≥ ( )1 12 2 2n n n nS S a a n− −− = − ≥ 12 2n n na a a −= − ( ) 1 2 2n n a na − = ≥ { }na ( )*2n na n N= ∈ ( )( )1 1k k k k nb a a a a k n+= ⋅ + + + ≤ ≤ ( )12 2 2 2k k k n kb += ⋅ + + + ( )12 1 2 2 1 2 k n k k − + − = ⋅ −  1 22 2n k k+ += − { }( )1kb k n≤ ≤ n ( ) ( )2 3 1 22 2 2 2 4 4 4n n n nT += + + + − + + +  ( ) ( )( )2 42 2 1 2 1 2 13 n n n n nT += ⋅ − − − + ( )24 2 2 3 2 13 n n nT = ⋅ − ⋅ + ( )( )14 2 1 2 13 n n nT += − − ( )( ) 11 2 3 2 3 1 1 4 2 1 2 14 2 1 2 1 n n n nn n nT ++ ⋅  = = − − −− −   2 1 1 2 2 2 2 3 114 2 1 n n n M T T T +  = + + + = − −  12 1 3n+ − ≥ 1 1 3 1 312 4 2 1 4n+  ≤ − < −  - 23 - 即 . 【点睛】本题考查了数列递推关系、等比数列的通项公式求和公式、裂项相消求和方法，考 查了推理能力与计算能力． 21.如图，已知抛物线 的焦点为 ，准线为 ，过点 的直线交抛物线于 ， 两点 ，点 在准线 上的投影为 ，若 是抛物线上一点，且 . （1）证明：直线 经过 的中点 ； （2）求 面积的最小值及此时直线 的方程. 【答案】（1）详见解析；（2）面积最小值为 16，此时直线方程为 . 【解析】 【分析】 （1）由题意得抛物线 的焦点坐标和准线方程，设 ，直线 ： ， 可得 的坐标，联立方程组，结合韦达定理，可得 的斜率和直线 的斜率，进而可得 直线 的方程，与抛物线联立可得两根之和，可得 中点 的纵坐标与 的相同，即可 证出直线 经过 的中点 ； （2）根据弦长公式求出 ，利用点到直线的距离公式，求出点 到直线 的距离为 ，运用 ，结合均值不等式求出 ，即可求出直 线 的方程. 【详解】解：（1）由题意得抛物线 的焦点 ，准线方程为 ， 设 ，直线 ： ， 1 3 2 4M≤ < 2 4y x= F l F A B B l E C AC EF⊥ BE AC M ABC∆ AC 3 0x y± − = 2 4y x= ( )2 ,2B t t AB 1x my= + E EF AC AC AC M B BE AC M 2 2 2 14 1 2AC t t t = + + + B AC d 1 162ABCS AC d∆ = ⋅ = t AD 2 4y x= ( )1,0F 1x = − ( )2 ,2B t t AB 1x my= + - 24 - 则 ， 联立 和 ， 可得 ， 显然 ，可得 ， 因为 ， ， 所以 ， 故直线 ： ， 由 ， 得 . ∴ ， ， 所以 的中点 的纵坐标 ，即 ， 所以直线 经过 的中点 . （2）所以 ， 设点 到直线 的距离为 ， ( )1,2E t− 1x my= + 2 4y x= 2 4 4y my= + 4 0A By y + = 2 1 2,A t t  −   EFk t= − AB EF⊥ 1 ACk t = AC 2 2 1 1y xt t t  + = −   2 2 4 12 0 y x x ty t  = − − − = 2 2 44 8 0y ty t − − − = 4A Cy y t+ = 2 48A Cy y t = − − AC M 2My t= M By y= BE AC M ( )22 21 1 4A C A C A Ct y y t y yA y yC = + − = + + − 2 2 2 14 1 2t t t = + + + B AC d - 25 - 则 . 所以 ， 当且仅当 ，即 ， 时，直线 的方程为： ， 时，直线 的方程为： . 另解： . 【点睛】本题考查直线与抛物线的位置关系，涉及直线方程、中点坐标公式、抛物线的标准 方程和性质、联立方程、韦达定理、弦长公式以及三角形面积公式，考查解题分析能力和计 算能力. 22.已知函数 ， 是 的导函数. （1）证明：当 时， 在 上有唯一零点； （2）若存在 ，且 时， ，证明： . 【答案】（1）见解析（2）见解析 【解析】 【分析】 （1）求出 ，当 时， 单调递增，利用 和 判断出 上有唯一零点．当 时， 的最小值大于零，则 在 上 没有零点.（2）令， ，将 转化为 ，再构造函数利用导数证明最小 值小于 0. 2 2 2 2 2 2 2 1 12 2 2 1 1 t t tt td t t − − − + + = = + + ( )3 32 2 1 12 2 2 2 2 162ABCS AC d t t∆  = ⋅ = + + ≥ + =   4 1t = 1t = ± 1t = AD 3 0x y− − = 1t = − AD 3 0x y+ − = 2 2 2 2 2 1 1 1 12 2 16 22 2ABC A CS BM y y t t tt t∆  = ⋅ − = + + − ⋅ + +   3 22 2 12 2t t  = + +   1( ) sin ln 12 2 mf x x x x= − − + ( )f x′ ( )f x 2m = ( )f x′ (0, )+∞ 1 2, (0, )x x ∈ +∞ 1 2x x≠ ( ) ( )1 2f x f x= 2 1 2x x m< ( )f x′ (0, )x π∈ ( )f x′ 03f π ′ <   ( ) 0f π′ > (0, )x π∈ [ , )x π∈ +∞ ( )f x′ ( )f x′ [ , )π +∞ 2 1 xt x = 2 1 2x x m< 1 ln t tt − > - 26 - 【详解】（1）证明：当 时， ， . 当 时， 为增函数，且 ， ， ∴ 在 上有唯一零点； 当 时， ， ∴ 在 上没有零点. 综上知， 在 上有唯一零点. （2）证明：不妨设 ，由 得 ， ∴ . 设 ，则 ，故 在 为增函数， ∴ ，从而 ， ∴ ， ∴ ， 下面证明： . 令 ，则 ，即证明 ，只要证明 .（*） 设 ，则 ，∴ 在 单调递减. 当 时， ，从而（*）得证，即 . ∴ ，即 . 【点睛】（1）零点问题可利用函数单调性和零点存在性定理来解决． （2）通过换元将两个变量转化为一个变量，构造函数，利用导数来证明不等式． 2m = 1( ) sin ln 12f x x x x= − − + 1 1( ) 1 cos2f x x x ′ = − − (0, )x π∈ ( )f x′ 1 3 3 31 03 4 4f π π π  ′ = − − = − <   3 1( ) 02f π π ′ = − > ( )f x′ (0, )π [ , )x π∈ +∞ 1 1( ) 1 cos2f x x x ′ = − − 1 1 1 11 02 2x π− − − >  ( )f x′ [ , )π +∞ ( )f x′ (0, )+∞ 1 20 x x< < ( ) ( )1 2f x f x= 1 1 1 1 sin ln 12 2 mx x x− − + 2 2 2 1 sin ln 12 2 mx x x= − − + ( ) ( )2 1 2 1 2 1 1ln ln sin sin2 2 m x x x x x x− = − − − ( ) sing x x x= − ( ) 1 cos 0g x x′ = −  ( )g x (0, )+∞ 2 2 1 1sin sinx x x x− > − 2 1 2 1sin sinx x x x− > − ( )2 1ln ln2 m x x− ( ) ( )2 1 2 1 2 1 1 1sin sin2 2x x x x x x= − − − > − 2 1 2 1ln ln x xm x x −> − 2 1 1 2 2 1ln ln x x x xx x − >− 2 1 xt x = 1t > 1 ln t tt − > 1ln 0tt t −− < 1( ) ln th t t t −= − ( )2 1 ( ) 0 2 t h t t t − ′ = − < ( )h t (1, )+∞ 1t > ( ) (1) 0h t h< = 2 1 1 2 2 1ln ln x x x xx x − >− 1 2m x x> 2 1 2x x m< - 27 - 本题是一道综合性的难题． - 28 -