- 10.85 MB
- 2021-06-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
存在性问题
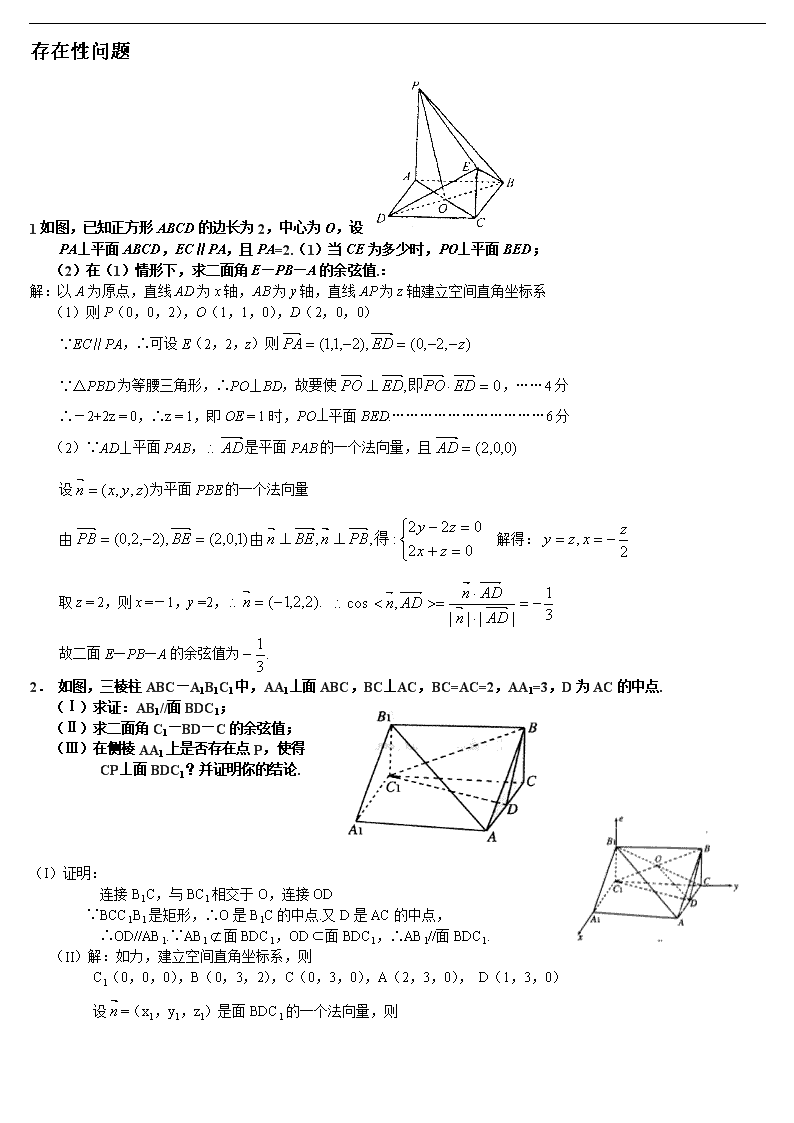
1如图,已知正方形 ABCD的边长为 2,中心为 O,设
PA⊥平面 ABCD,EC∥PA,且 PA=2.(1)当 CE为多少时,PO⊥平面 BED;
(2)在(1)情形下,求二面角 E—PB—A的余弦值.:
解:以 A为原点,直线 AD为 x轴,AB为 y轴,直线 AP为 z轴建立空间直角坐标系
(1)则 P(0,0,2),O(1,1,0),D(2,0,0)
∵EC∥PA,∴可设 E(2,2,z)则 ),2,0(),2,1,1( zEDPA
∵△PBD为等腰三角形,∴PO⊥BD,故要使 0, EDPOEDPO 即 ,……4分
∴-2+2z = 0,∴z = 1,即 OE = 1时,PO⊥平面 BED.……………………………6分
(2)∵AD⊥平面 PAB, AD 是平面 PAB的一个法向量,且 )0,0,2(AD
设 ),,( zyxn 为平面 PBE的一个法向量
由 )1,0,2(),2,2,0( BEPB 由
02
022
:,,
zx
zy
PBnBEn 得 解得:
2
, zxzy
取 z = 2,则 x =-1,y =2, ).2,2,1(n
3
1
||||
,cos
ADn
ADnADn
故二面 E—PB—A的余弦值为 .
3
1
2. 如图,三棱柱 ABC—A1B1C1中,AA1⊥面 ABC,BC⊥AC,BC=AC=2,AA1=3,D为 AC的中点.
(Ⅰ)求证:AB1//面 BDC1;
(Ⅱ)求二面角 C1—BD—C的余弦值;
(Ⅲ)在侧棱 AA1上是否存在点 P,使得
CP⊥面 BDC1?并证明你的结论.
(I)证明:
连接 B1C,与 BC1相交于 O,连接 OD
∵BCC1B1是矩形,∴O是 B1C的中点.又 D是 AC的中点,
∴OD//AB1.∵AB1面 BDC1,OD面 BDC1,∴AB1//面 BDC1.
(II)解:如力,建立空间直角坐标系,则
C1(0,0,0),B(0,3,2),C(0,3,0),A(2,3,0), D(1,3,0)
设 n =(x1,y1,z1)是面 BDC1的一个法向量,则
,
0
0
1
1
DCn
BCn
即 )
2
1,
3
1,1(
,03
023
11
11
n
yx
zy
取 .…………6分
易知 CC1 =(0,3,0)是面 ABC的一个法向量.
7
2
3
6
7
1
||||
,cos
1
1
1
CCn
CCnCCn ∴二面角 C1—BD—C的余弦值为
7
2
(III)假设侧棱 AA1上存在一点 P(2,y,0)(0≤y≤3),使得 CP⊥面 BDC1.
则
.
3
7
3
,
0)3(32
0)3(3
,
0
0
1
1
y
y
y
y
DCCP
BCCP
即
∴方程组无解.∴假设不成立. ∴侧棱 AA1上不存在点 P,使 CP⊥面 BDC1.
3 如图,已知四棱锥 S—ABCD的底面是边长为 4的正方形,S在底面上的射影 O落在正方形 ABCD内,且 O到 AB、
AD的距离分别为 2和 1.(I)求证 SCAB 是定值;
(II)已知 P是 SC的中点,且 SO=3,问在棱 SA上是否存在一点 Q,使得异面直线 OP与 BQ所成的角为 90°?若
存在,请给出证明,并求出 AQ的长;若不存在,请说明理由.
解:法一:(I)以 O为坐标原点,以 OS所在直线为 Oz轴,过 O且平行于 AD的直线为 Ox轴.过 O且平行于 AB的直线
为 Oy轴,建立如图所示空间直角坐标系……1分
设 S(0,0,z)(z>0,z∈R) 则 ),3,2(),0,4,0( zSCAB
12),3,2()0,4,0( zSCAB 即 SCAB 为定值.
(II)由(I)建立的空间直角坐标系可知 A(2,-1,0),B(2,3,0)C(-2,3,0),S(0,0,3)P(-1,
2
3,
2
3
)
设点 Q(x,y,z),则存在λ使 ASAQ
14
4
3312
4
3||
4
3||
)
4
9,
4
1,
2
1(,10
11
4
3068
0
2
9)4(
2
32
0)3,4,2()
2
3,
2
3,1(
)3,1,22(
10
3
1
22
1
22
)3,1,2(),1,2(
222
ASAQ
QSAQ
BQOP
Q
z
y
x
y
x
zyx
且上在棱知点由
分即
即
则
分即
即
法二:(I)证明:在△SDC内,作 SE⊥CD交 CD于 E,连结 OE……1分
∵SO⊥平面 ABCD ∴SO⊥CD ∴CD⊥平面 SOE ∴SO⊥OE
∴OE//AD ∴DE=1 从而 CE=3
1234||||cos|||| ECDCSCESCDCSCDCSCAB 即 SCAB 为定值.
4. 直三棱柱 ABC—A1B1C1中,∠ACB=90°,BC=AC=2,AA1=4,D为棱 CC1上的一动点,M、N 分别为△ABD、
△A1B1D的重心.
(Ⅰ)求证:MN⊥AB;
(Ⅱ)若二面角 C—AB—D的正切值为 2 ,
求二半平面 ABD、A1B1D所成锐二面
角的余弦值;
(Ⅲ)若点 C1在平面 A1B1D上的射影正好为 N,
试判断 C在平面 ABD上的射影是否为M?
并说明理由.
.解:(I)以 C1为原点,C1A1为 x轴,C1B1为 y轴,C1C为 z轴建立坐标系.
设 C1D=a(0≤a≤4),由题意有
C1(0,0,0),A1(2,0,0),B1(0,2,0),C(0,0,4),A(2,0,4)
B(0,2,4),D(0,0,a).………………………………………………1分
∵M、N分别为△ABD,△A1B1D的重心,
分
分
分
4.,,0
3),0,2,2()
3
8,0,0(
2),
3
,
3
2,
3
2(),
3
8,
3
2,
3
2(
MNABMNABMNAB
ABMN
aNaM
(注:也可以不用向量证法)
(II)平面 ABC法向量 1n =(0,0,1),设平面 ABD的法向量 2n =(x1,y1,z1),则
……………………12分
分得令
分
即
6).1,
2
4,
2
4(,1
5
.0),,()0,2,2(
,0),,()4,0,2(
,0
,0
21
111
111
2
2
aanz
zyx
zyxa
nAB
nAD
设二面角 C—AB—D的大小为θ,则由
3
3cos,2tan 得
3
3
1)
2
4()
2
4(
1
||||
||cos
2221
21
aann
nn
,
解得 a=2,(a=6舍去),∴ 2n =(-1,-1,1).……………………………………7分
设平面 A1B1D的法向量
).1,1,1(,1
8
.022
,022
,0),,()0,2,2(
,0),,()2,0,2(
,0
,0
),,,(
3
311
31
3
nz
yx
zx
zyx
zyx
nBA
nDA
zyxn
则令
分得即
则
∴半平面 ABD,A1B1D所成锐二面角的余弦值
为:
3
1
33
|111|
||||
||
32
32
nn
nn
.
(III)若点 C1在平面 A1B1D上的射影正好为 N,则
0),0,2()
3
,
3
2,
3
2(
,0, 1111
aa
DANCDANC
即
即
解得 a=2(a=-2 舍去).
∵D为 CC1的中点,根据对称性知 C在平面 ABD上的射影正好为M.……12分
5. 如图,在四棱锥 P—ABCD中,底面 ABCD是矩形,PA⊥平面 ABCD,PA=AD,AB= 2 AD,E是线段 PD上的点,
F是线段 AB上的点,且 ).0(
FA
BF
ED
PE
(I)判断 EF与平面 PBC的关系,并证明;
(II)当λ=1时,证明 DF⊥平面 PAC;
(III)是否存在实数λ,使异面直线 EF与 CD所成角为 60°?
若存在,试求出λ的值;若不存在,请说明理由.
(本小题满分 12分)
解:(I)EF∥平面 PBC. 证明如下
作 FG∥BC交 CD于 G,连结 EG,则
FA
BF
ED
PE
GD
CG
FA
BF
∴
GD
CG
ED
PE
∴PC∥EG 又 FG∥BC,BC∩PC=C,FG∩GE=G.
∴平面 PBC∥平面 EFG.又 EF平面 EFG∴EF∥平面 PBC
(II)λ=1,则 F为 AB的中点又 AB= 2 AD AF=
2
1
AB
∴在 Rt△FAD与 Rt△ACD中 2
2
2
tan
AD
AD
AF
ADAFD 22tan
AD
AD
AD
CDCAD
∴∠AFD=∠CAD ∴AC⊥DF 又∵PA⊥平面 ABCD,DF平面 ABCD ∴PA⊥DF.
∴DF⊥平面 PAC
(III)建立如图所示空间填角坐标系,设 PA=AD=1,则 A(0,0,0),B( 2 ,0,0),D(0,1,0),C( 2 ,1,
0),P(0,0,1)又 )0(
FA
BF
ED
PE
)0,0,
1
2(
F ……………………8分
设 ),,0( 00 zyE 则
1
1
1
),1,0()1,,0(
)0(
),1,0(),1,,0(
0
0
0000
0000
z
y
zyzy
EDPE
ED
PE
zyEDzyPE
即又
即 )
1
1,
1
,0(
E )
1
1,
1
,
1
2(
EF
)0,0,2(CD 假设存在实数λ,使异面直线 EF与 CD所成的角为 60°,则
2
1
3
2
2
1
3
|
1
2|
||||
||60cos
22
CDEF
CDEF
552
∴存在实数 5 使异面直线 EF与 CD所成的角为 60°
6.
如图,四棱锥P—ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA = AD = CD = 2AB = 2,M为PC的中点.
(1)求证:BM∥平面PAD;
(2)平面PAD内是否存在一点N,使MN⊥平面PBD?若存在,确定N的位置,若不存在,说明理由;
(3)求直线PC与平面PBD所成的角的正弦值.
.解:(1)取 PD的中点 E,连 EM、AM,
2
∵M是 PC的中点,∴EM CD
2
1
又 AB CD
2
1
∴AB EM, ∴ABME是平行四边形,
∴BM∥AE,∴BM∥平面 PAD.
(2)以 A为原点,以 AB,AD,AP分别为 x轴,y轴,z轴,
建立空间直角坐标系
则 B(1,0,0),D(0,2,0),P(0,0,2),C(2,2,0),∴M(1,1,1), )2,0,1(),0,2,1( PBBD
设 ),,0( zyN 则 )1,1,1( zyMN ,若 MN⊥平面 PBD则 MN⊥BD,MN⊥PB.
2
1,
2
1
0)1(21
0)1(21
0
0
zy
z
y
PBMN
BDMN
, ).
2
1,
2
1,0(N
∴在平面 PAD内存在一点 )
2
1,
2
1,0(N 、使 MN⊥面 PBD
(3)设平面 PBD的法向量为 n,令 )2,2,2(),
2
1,
2
1,1( PCMNn ,
3
2
32
2
6
112,cos
nPC ,∴直线 PC与面 PBD所成角正弦值为
3
2
与三视图有关
1.(本小题满分 12分)
直三棱柱 A1B1C1—ABC的三视图如图所示,D、E分别为棱 CC1和 B1C1的中点。
(1)求点 B到平面 A1C1CA的距离;
(2)求二面角 B—A1D—A的大小;
(3)在 AC上是否存在一点 F,使 EF⊥平面 A1BD,若存在确定其位置,若不存在,说明理由.
20.解:(1)由已知得:CA=CB=CC1=2,∠ACB=90°
∴BC⊥AC
∴BC⊥平面 A1C1CA
∴点 B到平面 A1C1CA的距离为 2
(2)如图建立空间直角坐标系
则 B(0,2,0)D(0,0,1)A1(2,0,2)
)2,2,2()1,0,2( 11 DADA
设平面 A1DB的法向量为 ),,1(1 yxn
则
1
2
0222
02
x
y
yx
y
)2,1,1(1 n
而平面 ACC1A1的法向量为 )0,1,0(2n 6
1cos 21
nn ∴二面角 B—A1D—A的大小为
6
6arccos
(3)存在 F为 AC的中点,使 EF⊥平面 A1BD设 F(x,0,0),由 E(0,1,2)得 )2,1,( xEF
若 EF⊥平面 A1BD,则 1// nEF 由 )2,1,1(1 n 得 x=1
∴F为 AC的中点∴存在 F为 AC的中点,使 EF⊥平面 A1BD
2.(本小题满分 12分)
一个多面体的三视图及直观图如图所示,M、N分别是 A1B、B1C1的中点。
(Ⅰ)求证:MN⊥平面 A1BC;(Ⅱ)求异面直线 AM和 CA1所成的角;(Ⅲ)求二面角 A—A1B—C的大小.
解:由三视图可知,在这个多面体的直观图中,AA1⊥平面 ABC。
且 AC⊥BC,AC=BC=CC1=a
(Ⅰ)连结 AC1,AB1,因为 BC⊥平面 ACC1A1,所以 BC⊥AC1。
在正方形 ACC1A1中,A1C⊥AC1
又因为 BC∩A1C=C,所以 AC1⊥平面 A1BC
由矩形性质得,AB1过 A1B的中点M,
在△AB1C1中,由中位线性质得MN//AC1,
得MN⊥平面 A1BC
(Ⅱ)由题意 CB,CA,CC1两两垂直,故以 C为原点,CB,CA,CC1所在直
线分别为 x轴,y轴,z轴,建立空间直角坐标系,又 AC=BC=CC1=a,则
B(a,0,0)B1(a,0,a),A(0,a,0),C(0,0,0),C1(0,0,a),
A1(0,a,a),则 )
2
,
2
,
2
( aaaM
0
),,0(),
2
,
2
,
2
(
1
1
CAAM
aaCAaaaAM
∴异面直线 AM和 CA1所成的角为 90°
(Ⅲ)AB中点 E的坐标为( )0,
2
,
2
aa
)0,
2
,
2
(),,,0(1
aaCEaaAC 易知 为平面 AA1B的法向量.
又 AC1⊥平面 A1BC,故 1AC 为平面 A1BC的法向量 设二面角 A—A1B—C为θ,则
2
1|
2
2
2
2||
||||
||,cos||cos|
2
1
1
1
aa
a
ACCE
ACCE
CACE
由题意可知, 6060 1 为——,即二面角为为锐角,所以 CBAA ……12分
3. 某几何体的三视图如图所示,P是正方形 ABCD对角线的交点,G是 PB的中点。
(Ⅰ)根据三视图,画出该几何体的直观图;
(Ⅱ)在直观图中,①证明:PD//面 AGC;
②证明:面 PBD⊥AGC
③求面 PAB与面 PBC的夹角的余弦值。
.解:(Ⅰ)该几何体的直观图如图所示。 …………3分
(2)①证明:连结 AC,BD交于点 O,连结 OG,因为 G为 PB的中点,
O为 BD的中点,所以 OG//PD。又 OG面 AGC,PD面 AGC,
所以 PD//面 AGC。 ………………文 8分,理 6分
②连结 PO,由三视图,PO⊥面 ABCD,所以 AO⊥PO。 又 AO⊥BO,
所以 AO⊥面 PBD。 因为 AO面 AGC,所以面 PBD⊥面 AGC …文 12分,理 9分
(理)③建立如图所示坐标系,由三视图知,PO= 2 ,AB=2,AC=2 2 ,AO= 2 ,
∴P(0,0, 2 ),B(0, 2 ,0),A( 2 ,0,0),
C(- 2 ,0,0), )2,2,0( BP
)0,2,2(),0,2,2( BCBA
设面 PBA的法向量为 n=(x,y,z)
∴
022
022
0
0
yx
zy
BAn
BPn
,即
令 x=1得 y=1,z=1。
∴n=(1,1,1)
设面 PBC的法向量为 zyx ,,(m )
∴
022
022
0
0
yx
zy
BCm
BPm
,即
令 1,11 zyx 得
∴m=(1,-1,-1)。
设面 PAB与 PBC的夹角为θ,
则
3
1
33
111
||||
cos
nm
nm
所以面 PAB与 PBC的夹角为余弦值为
3
1
………………理 12分
4.(本小题满分 12分)
一个多面体的直观图及三视图如图所示:(其中 E、F分别是 PB、AD的中点)
(Ⅰ)求异面直线 PD与 AE所成角的余弦值;
(Ⅱ)求证:EF⊥平面 PBC;
(Ⅲ)求三棱锥 B—AEF的体积。
2
.解证:(Ⅰ)依题意知该多面体是底面为正方形的
四棱锥,且 PD⊥底面 ABCD,PD=DC=a 取 BD中点 O,连接 EO,则 DO//PD,EO⊥底面 ABCD,
2
aEO
所以∠AEO的为异面直线 PD与 AE所成的角。 ……4分
在 Rt△AOE中, ,
2
2,
2
aAOaOE aAOOEAE
2
322
所以 .
3
3
2
3
2cos
a
a
AE
OEAEO 即异面直线 PD与 AE所成角的余弦值为
3
3
(Ⅱ)取 PC的中点 G,连结 EG,GD,则
.//
2
1// DFGEBCEG
,所以
由(Ⅰ)知 FD⊥平面 PDC, DG 面 PDC,
所以 FD⊥DG。
所以四边形 FEGD为矩形,因为 G为等腰
Rt△RPD斜边 PC的中点,所以 DG⊥PC,
又 DG⊥GE,PC∩EG=E
所以 DG⊥平面 PBC,因为 DG//EF
所以 EF⊥平面 PBC。 ……………………10分
(Ⅲ)
32
24
1
2
1
4
1
3
1
3
1 aaaOESVV ABFABFEAEFB …………12分
1
相关文档
- 高考数学专题复习练习第六章 第三2021-06-116页
- 高考数学专题复习练习选修4-2 矩阵2021-06-115页
- 高考数学专题复习练习:4-5 专项基2021-06-116页
- 高考数学专题复习练习:8_5 直线、2021-06-1121页
- 高考数学专题复习练习第二章 第五2021-06-116页
- 高考数学专题复习练习:7_1 不等关2021-06-1113页
- 高考数学专题复习练习第四章 第四2021-06-114页
- 高考数学专题复习练习第九章 第三2021-06-115页
- 高考数学专题复习练习:7-2 专项基2021-06-115页
- 高考数学专题复习练习:1-1 专项基2021-06-104页