高中数学（人教版a版必修三）配套课时作业：第三章 概率 3.3.2 均匀随机数的产生 5页

3.3.2 均匀随机数的产生 课时目标 1.了解均匀随机数的产生方法与意义.2.会用模拟实验求几何概型的概率.3.能 利用模拟实验估计不规则图形的面积． 1．均匀随机数的产生 (1)计算器上产生[0,1]的均匀随机数的函数是______________函数． (2)Excel软件产生[0,1]区间上均匀随机数的函数为“rand()”． 2．用模拟的方法近似计算某事件概率的方法 (1)____________的方法：制作两个转盘模型，进行模拟试验，并统计试验结果． (2)____________的方法：用 Excel软件产生[0,1]区间上均匀随机数进行模拟．注意操作步 骤． 3．[a，b]上均匀随机数的产生． 利用计算器或计算机产生[0,1]上的均匀随机数 x＝RAND，然后利用伸缩和平移交换，x ＝x1*(b-a)+a就可以得到［a,b］内的均匀随机数，试验的结果是［a,b］上的任何一个实数， 并且任何一个实数都是等可能的. 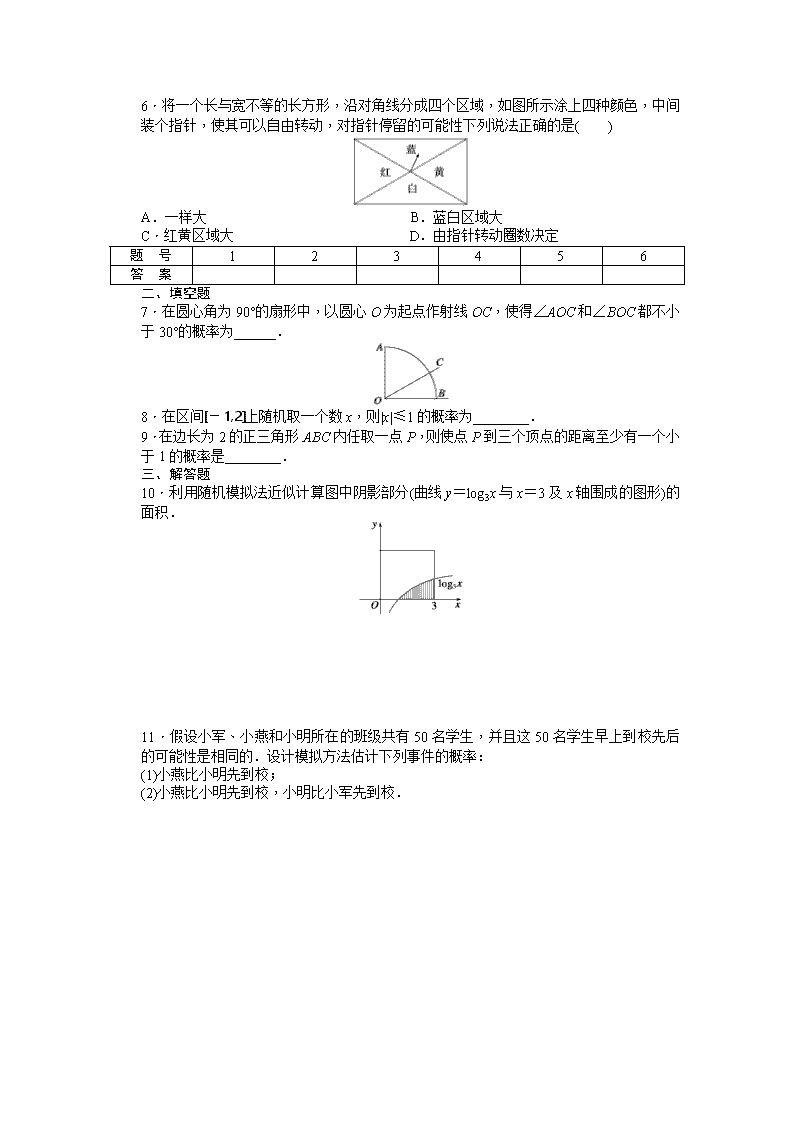一、选择题 1．将[0,1]内的均匀随机数转化为[－3,4]内的均匀随机数，需要实施的变换为( ) 2．在线段 AB上任取三个点 x1，x2，x3，则 x2位于 x1与 x3之间的概率是( ) A.1 2 B.1 3 C.1 4 D．1 3．与均匀随机数特点不符的是( ) A．它是[0,1]内的任何一个实数 B．它是一个随机数 C．出现的每一个实数都是等可能的 D．是随机数的平均数 4．如图，边长为 2的正方形中有一封闭曲线围成的阴影区域，在正方形中随机撒一粒豆 子，它落在阴影区域内的概率为 2 3 ，则阴影区域的面积为( ) A.4 3 B.8 3 C.2 3 D．无法计算 5．在长为 12 cm的线段 AB上任取一点 M，并以线段 AM为边作正方形．这个正方形的 面积介于 36 cm2与 81 cm2之间的概率为( ) A.36 81 B.12 36 C.12 81 D.1 4 6．将一个长与宽不等的长方形，沿对角线分成四个区域，如图所示涂上四种颜色，中间 装个指针，使其可以自由转动，对指针停留的可能性下列说法正确的是( ) A．一样大 B．蓝白区域大 C．红黄区域大 D．由指针转动圈数决定 题 号 1 2 3 4 5 6 答 案 二、填空题 7．在圆心角为 90°的扇形中，以圆心 O为起点作射线 OC，使得∠AOC和∠BOC都不小 于 30°的概率为______． 8．在区间[－1,2]上随机取一个数 x，则|x|≤1的概率为________． 9．在边长为 2的正三角形 ABC内任取一点 P，则使点 P到三个顶点的距离至少有一个小 于 1的概率是________． 三、解答题 10．利用随机模拟法近似计算图中阴影部分(曲线 y＝log3x与 x＝3及 x轴围成的图形)的 面积． 11．假设小军、小燕和小明所在的班级共有 50名学生，并且这 50名学生早上到校先后的 可能性是相同的．设计模拟方法估计下列事件的概率： (1)小燕比小明先到校； (2)小燕比小明先到校，小明比小军先到校． 能力提升 12．如图所示，曲线 y＝x2与 y轴、直线 y＝1围成一个区域 A(图中的阴影部分)，用模拟 的方法求图中阴影部分的面积(用两种方法)． 13．甲、乙两人约定在 6时到 7时之间在某处会面，并约定先到者应等候另一人一刻钟， 过时即可离去．求两人能会面的概率(用两种方法)． 1．[0,1]或[a，b]上均匀随机数的产生 利用计算器的 RAND函数可以产生[0,1]的均匀随机数，试验的结果是区间[0,1]内的任何一 个实数，而且出现任何一个实数是等可能的，因此，可以用计算器产生的 0到 1之间的均 匀随机数进行随机模拟． 计算器不能直接产生[a，b]区间上的随机数，但可利用伸缩和平移变换得到：如果 Z是[0,1] 区间上的均匀随机数，则 a＋(b－a)Z就是[a，b]区间上的均匀随机数． 2．随机模拟试验是研究随机事件概率的重要方法．用计算机或计算器模拟试验，首先把 实际问题转化为可以用随机数来模拟试验结果的概率模型，也就是怎样用随机数刻画影响 随机事件结果的量．我们可以从以下几个方面考虑： (1)由影响随机事件结果的量的个数确定需要产生的随机数的组数．如长度、角度型只用一 组，面积型需要两组． (2)由所有基本事件总体对应区域确定产生随机数的范围． (3)由事件 A发生的条件确定随机数所应满足的关系式． 答案： 3．3.2 均匀随机数的产生 知识梳理 1．(1)RAND 2.(1)试验模拟 (2)计算机模拟 作业设计 1．C [根据伸缩、平移变换 a＝a1*［4-(-3)］+(-3)=a1*7-3.］ 2．B [因为 x1，x2，x3是线段 AB上任意的三个点，任何一个数在中间的概率相等且都 是 1 3 .] 3．D [A、B、C 是均匀随机数的定义，均匀随机数的均匀是“等可能”的意思，并不是“随 机数的平均数”．] 4．B [∵ S 阴影 S 正方形 ＝ 2 3 ，∴S 阴影＝ 2 3 S 正方形＝ 8 3 .] 5．D [由题意知，6