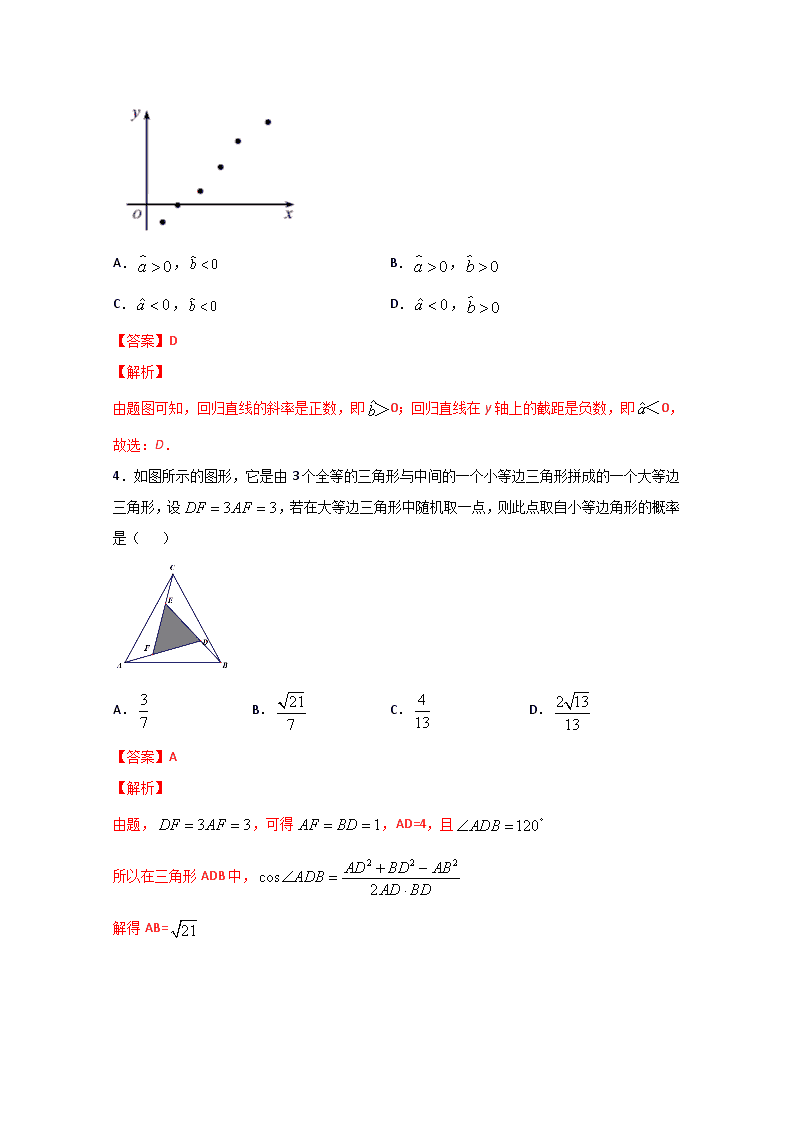第11章检测A卷（文）-2020年领军高考数学一轮复习（文理通用） Word版含解析 15页

第 11 章检测卷 A 卷 姓名 班级 准考证号 1．《易经》是我国古代预测未来的著作，其中同时抛掷三枚古钱币观察正反面进行预测未知， 则抛掷一次时出现两枚正面一枚反面的概率为（ ） A． 1 8 B． 1 4 C． 3 8 D． 1 2 【答案】C 【解析】 抛掷三枚古钱币出现的基本事件共有：正正正，正正反，正反正，反正正，正反反，反正反， 反反正，反反反 8 中，其中出现两正一反的共有 3 种，故概率为 3 8 . 故选 C 2．某班全体学生测试成绩的频率分布直方图如图，数据的分组依次为： 20,40 ， 40,60 ，  60,80 ， 80,100 ．若高于80 分的人数是15 ，则该班的学生人数是（ ） A． 40 B． 45 C．50 D． 60 【答案】C 【解析】 由题意，根据给定的频率分布直方图，可得在 80,100 之间的频率为 20 0.0015 0.3  ， 又由高于80 分的人数是15 ，则该班的学生人数是 15 500.3  人，故选 C． 3．已知变量 x ，y 之间具有线性相关关系，其散点图如图所示，回归直线l 的方程为  y bx a  ， 则下列说法正确的是（ ） A．  0a  ， 0b  B．  0a  ， 0b  C． ˆ 0a  ， 0b  D． ˆ 0a  ， 0b  【答案】D 【解析】 由题图可知，回归直线的斜率是正数，即 ˆb＞0；回归直线在 y 轴上的截距是负数，即 ˆa＜0， 故选：D． 4．如图所示的图形，它是由 3 个全等的三角形与中间的一个小等边三角形拼成的一个大等边 三角形，设 3 3DF AF  ，若在大等边三角形中随机取一点，则此点取自小等边角形的概率 是（ ） A． 3 7 B． 21 7 C． 4 13 D． 2 13 13 【答案】A 【解析】 由题， 3 3DF AF  ，可得 1AF BD  ，AD=4，且 120ADB   所以在三角形 ADB 中， 2 2 2 cos 2 AD BD ABADB AD BD     解得 AB= 21 所以概率为 2 2 3 9 34 21 73 4 DF P AB    故选：A 5．下表是降耗技术改造后生产甲产品过程中记录的产量 x （吨）与相应的生产能耗 y （吨标 准煤）的几组对应数据，根据表中提供的数据，求出 y 关于 x 的线性回归方程为 0.7 0 35ˆ .xy   ，则表中 m 的值为（ ） x 3 4 5 6 y 2.5 m 4 4.5 A．3 B．3.5 C．4 D．4.5 【答案】A 【解析】 由题意，根据所给的表格可以求出： 3 4 5 6 2.5 4 4.5 114.5,4 4 4 m mx y          ， 又因为这组数据的样本中心点 11(4.5, )4 m 在线性回归直线上， 即11 0.7 4.5 0.354 m    ，解得 3m  ，故选 A． 6．《九章算术》中有如下问题：“今有勾五步，股一十二步，问勾中容圆，径几何？ ”其大意： “已知直角三角形两直角边长分别为 5 步和 12 步，问其内切圆的直径为多少步？”现若向此三 角形内随机投一粒豆子，则豆子落在其内切圆外的概率是 ( ) A． 2 15  B． 3 20  C． 21 15  D． 31 20  【答案】C 【解析】 如图所示，直角三角形的斜边长为 2 25 12 13  ， 设内切圆的半径为 r ，则5 12 13r r    ，解得 2r = . 所以内切圆的面积为 2 4r  ， 所以豆子落在内切圆外部的概率 4 2P 1 11 155 122        ，故选 C。 7．如图，在边长为 2 的正方形中，随机撒 1000 粒豆子，若按π≈3 计算，估计落到阴影部分的 豆子数为（ ） A．125 B．150 C．175 D．200 【答案】A 【解析】 由题意知圆的半径为 1，则圆的面积近似为 3， 又正方形面积为 4，则阴影部分面积为 1 1(4 3) 0.52 2    . 设落到阴影部分的豆子数为 n ， 则 1 2 , 1251000 4 n n  ． 故选：A． 8．3 名同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公 益活动的概率为（ ）. A． 1 4 B． 2 3 C． 1 2 D． 3 4 【答案】D 【解析】 3位同学各自在周六、周日两天中任选一天参加公益活动，共有 32 8 种情况 周六、周日都有同学参加公益活动，共有 32 2 8 2 6    种情况 所求概率为 6 3 8 4  本题正确选项： D 9．如图是某手机商城 2018 年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图 （如：第三季度华为销量约占50% ，三星销量约占30% ，苹果销量约占 20% ），根据该图， 以下结论中一定正确的是（ ） A．四个季度中，每季度三星和苹果总销量之和均不低于华为的销量 B．苹果第二季度的销量小于第三季度的销量 C．第一季度销量最大的为三星，销量最小的为苹果 D．华为的全年销量最大 【答案】D 【解析】 对于 A ，第四季度中，华为销量大于50% ，三星和苹果总销量之和低于华为的销量，故 A 错 误； 对于 B ，苹果第二季度的销量大于苹果第三季度的销量，故 B 错误； 对于C ，第一季度销量最大的是华为，故C 错误； 对于 D ，由图知，四个季度华为的销量都最大，所以华为的全年销量最大， D 正确， 故选 D. 10．五行学说是华夏民族创造的哲学思想，是华夏文明重要组成部分.古人认为，天下万物皆 由金、木、水、火、土五类元素组成，如图，分别是金、木、水、火、土彼此之间存在的相 生相克的关系.若从 5 类元素中任选 2 类元素，则 2 类元素相生的概率为（ ） A． 1 2 B． 1 3 C． 1 4 D． 1 5 【答案】A 【解析】 金、木、水、火、土任取两类，共有： 金木、金水、金火、金土、木水、木火、木土、水火、水土、火土 10 种结果， 其中两类元素相生的有火木、火土、木水、水金、金土共 5 结果， 所以 2 类元素相生的概率为 5 1 10 2  ，故选 A. 11．一般来说，一个班级的学生学号是从 1 开始的连续正整数，在一次课上，老师随机叫起 班上 8 名学生，记录下他们的学号是：3、21、17、19、36、8、32、24，则该班学生总数最 可能为（ ） A．39 人 B．49 人 C．59 人 D．超过 59 人 【答案】A 【解析】 因为随机抽样中，每个个体被抽到的机会都是均等的， 所以1 10: ，11 20: ， 21 30 ，31 40 ，….，每组抽取的人数，理论上应均等； 又所抽取的学生的学号按从小到大顺序排列为 3、8、17、19、21、24、32、36，恰好使1 10: ， 11 20: ， 21 30 ，31 40 四组中各有两个，因此该班学生总数应为 40 左右； 故选 A 12．设函数 2( ) 2 3f x x x   ，若从区间[ 2,4] 上任取一个实数 x ，则所选取的实数 x 满足 ( ) 0f x  的概率为（ ） A． 1 2 B． 1 3 C． 2 3 D． 1 4 【答案】C 【解析】 由题意，函数 2( ) 2 3f x x x   ， 令 ( ) 0f x  ，即 2 2 3 0x x   ，解得 1 3x   ， 根据长度比的几何概型可得概率为 3 ( 1) 2 4 ( 2) 3P     ，故选 C． 13．如图，在边长为 2 的正方形 ABCD 中，以 AB 的中点O为圆心，以 2 为半径作圆弧， 交边 ,AD BC 于点 ,M N ，从正方形 ABCD 中任取一点，则该点落在扇形OMN 中的概率为_ ____． 【答案】 8  【解析】 如图，正方形面积 2 2 4S    ，因 2, 1OM OA  ，故 1AM  ， 所以 4AOM   ，同理 4NOB   ，所以 2MON   ， 又 2OM  ，∴ 21 ( 2)2 2 2S     扇形MON ． ∴从正方形 ABCD 中任取一点，则该点落在扇形 OMN 中的概率为 2 4 8P    ． 故答案为： 8  ． 14．交通管理部门为了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、 丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为 ，其中甲社区有驾驶员 9 6 人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为 12，21，25，43，则这四个社 区驾驶员的总人数 的值为______． 【答案】808 【解析】 由题意可得抽样比为： 本题正确结果： 15．某工厂甲，乙，丙三个车间生产同一种产品，数量分别为 120 件，80 件，60 件.现用分层 抽样抽取一个容量为 n 的样本进行调查，其中从乙车间的产品中抽取了 4 件，则 n  ______. 【答案】13 【解析】 根据分层抽样的概念得到从各个车间应该抽取的数量为： , , ,a b c : : 6: 4:3a b c  ,其中 4, 6, 3, 13.b a c n     故答案为：13. 16．成都某市区 三所学校进行高三联考后，准备用分层抽样的方法从所有参考的高三理 科学生中抽取容量为 的样本进行成绩分析，已知 三所学校参考的理科学生分别有 人， 人， 人，则应从 校中抽取的学生人数为__________． 【答案】50 【解析】 ∵A，B，C 三所学校参考的理科学生分别有 300 人，400 人，500 人， ∴应从 C 校中抽取的学生人数为 120 50， 故答案为：50． 17．李克强总理在 2018 年政府工作报告指出，要加快建设创新型国家，把握世界新一轮科技 革命和产业变革大势，深入实施创新驱动发展战略，不断增强经济创新力和竞争力.某手机生 产企业积极响应政府号召，大力研发新产品，争创世界名牌.为了对研发的一批最新款手机进 行合理定价，将该款手机按事先拟定的价格进行试销，得到一组销售数据 ( , )( 1,2,...,6)i ix y i  ，如表所示： 单价 x （千元） 3 4 5 6 7 8 销量 y （百件） 70 65 62 59 56 t 已知 6 1 1 606 i i y y    . （1）若变量 x ， y 具有线性相关关系，求产品销量 y （百件）关于试销单价 x （千元）的线 性回归方程 y bx a $ $ $； （2）用（1）中所求的线性回归方程得到与 ix 对应的产品销量的估计值 ˆiy .当销售数据 ( , )i ix y 对应的残差的绝对值 ˆ 1i iy y  时，则将销售数据 ( , )i ix y 称为一个“好数据”.现从6个销售数 据中任取 3个，求“好数据”至少 2 个的概率. （参考公式：线性回归方程中b ， a 的估计值分别为 1 22 1 n i i i n i i x y nxy b x nx         ， a y bx $ $ ）. 【答案】（1） ˆ 4 82y x   ；（2） 4 5 . 【解析】 （1）由 6 1 1 606 i i y y    ，可得： 70 65 62 59 56 606 t      ，解得： 48t  1 1910 n i i i x y    ， =1980nxy ， 2 1 199 n i i x   ， 2 =181.5nx 代入可得 1 22 1 1910 1980 70 4199 181.5 17.5 n i i i n i i x y nxy b x nx             ˆˆ 60 4 5.5 82a y bx      线性回归方程为 ˆ 4 82y x   （2）利用（1）中所求的线性回归方程 ˆ 4 82y x   可得： 当 1 3x  时， 1ˆ 70y  ；当 2 4x  时， 2ˆ 66y  ；当 3 5x  时， 3ˆ 62y  ； 当 4 6x  时， 4ˆ 58y  ；当 5 7x  时， 5ˆ 54y  ；当 6 8x  时， 6ˆ 50y  与销售数据对比可知满足  ˆ| | 1 1,2, ,6i iy y i    的共有 4 个“好数据”： (3,70) 、 (4,65) 、 (5,62) 、 (6,59) 6个销售数据中任取3个共有： 3 6 20C  种取法 其中只有1个好数据的取法有 1 4C 4 种取法 至少 2 个好数据的概率为： 4 41 20 5P    18．根据调查，某学校开设了“街舞”、“围棋”、“武术”三个社团，三个社团参加的人数如下表所 示： 社团 街舞 围棋 武术 人数 320 240 200 为调查社团开展情况，学校社团管理部采用分层抽样的方法从中抽取一个容量为 n 的样本， 已知从“围棋”社团抽取的同学比从“街舞”社团抽取的同学少 2 人. （1）求三个社团分别抽取了多少同学； （2）若从“围棋”社团抽取的同学中选出 2 人担任该社团活动监督的职务，已知“围棋”社团被 抽取的同学中有 2 名女生，求至少有 1 名女同学被选为监督职务的概率。 【答案】（1）8,6,5（2） 3 5 . 【解析】 （1）设抽样比为 x，则由分层抽样可知，“街舞”、“围棋”、“武术”三个社团抽取的人数分别为 32 0x、240x、200x． 则由题意得 320x﹣240x＝2，解得 x 1 40  ． 故“街舞”、“围棋”、“武术”三个社团抽取的人数分别为 320 1 40   8、240 1 40   6、200 1 40   5． （2） 由（1）知，从“围棋”社团抽取的同学为 6 人， 其中 2 位女生记为 ,A B ;4 位男生记为 , , ,C D E F ; 从中选出 2 人担任该社团活动监督的职务有 15 种不同的结果，                               , , , , , , , , , , , , , , , , , , , , , , , , , , , , , A B A C A D A E A F B C B D B E B F C D C E C F D E D F E F 至少有 1 名女同学被选为监督职务有 9 种不同的结果，                  , , , , , , , , , , , , , , , , , ,A B A C A D A E A F B C B D B E B F 所以至少有 1 名女同学被选为监督职务的概率 3 5 . 19．为增强市民的环境保护意识，某市面向全市学校征召 100 名教师做义务宣传志愿者，成 立环境保护宣传组，现把该组的成员按年龄分成 5 组，如下表所示： 组别 年龄 人数 1  20,25 5 2  20,30 35 3  30,35 20 4  35,40 30 5  40,45 10 （Ⅰ）若从第 3，4，5 组中用分层抽样的方法选出 6 名志愿者参加某社区宣传活动，应从第 3， 4，5 组各选出多少名志愿者？ （Ⅱ）在Ⅰ的条件下，宣传组决定在这 6 名志愿者中随机选 2 名志愿者介绍宣传经验. （ⅰ）列出所有可能结果； （ⅱ）求第 4 组至少有 1 名志愿者被选中的概率。 【答案】（Ⅰ ）2,3,1（Ⅱ）（i）见解析（ii） 4 5 【解析】 （Ⅰ ）从第 3，4，5 组中用分层抽样的方法抽取 6 名志愿者参加某社区的宣传活动， 由频率分布图得： 应从第 3 组抽取：6 20 60   2 名志愿者， 应从第 4 组抽取：6 30 60   3 名志愿者， 应从第 5 组抽取：6 10 60   1 名志愿者． （Ⅱ）（ⅰ）记第 3 组的 2 名志愿者为 A1，A2，第 4 组的 3 名志愿者为 B1，B2，B3 第 5 组的 1 名志愿者为 C1． 则从 6 名志愿者中抽取 2 名志愿者有： （A1，A2），（A1，B1），（A1，B2），（A1，B3），（A1，C1）， （A2，B1），（A2，B2），（A2，B3），（A2，C1）， （B1，B2），（B1，B3），（B1，C1）， （B2，B3）（B2，C1）， （B3，C1）， 共有 15 种． （ⅱ）第 4 组没有志愿者被选中包括（A1，A2），（A1，C1），（A2，C1），共三种， 故第 4 组至少有 1 名志愿者被选中的概率 3 41 15 5   20．“微信运动”已经成为当下最热门的健身方式，小李的微信朋友圈内也有大量的好友参加了 “微信运动”.他随机的选取了其中 30 人，记录了他们某一天走路的步数，将数据整理如下： 步数  0,5000  5001,8000  8001, 人数 5 13 12 （1）若采用样本估计总体的方式，试估计小李所有微信好友中每日走路步数超过 5000 步的 概率； （2）已知某人一天的走路步数若超过 8000 步则他被系统评定为“积极型”，否则评定为“懈怠 型”，将这 30 人按照“积极型”、“懈怠型”分成两层，进行分层抽样，从中抽取 5 人，将这 5 人 中属于“积极型”的人依次记为  1,2,3iA i   ，属于“懈怠型”的人依次记为  1,2,3iB i   ， 现再从这 5 人中随机抽取 2 人接受问卷调查.设 M 为事件“抽取的 2 人来自不同的类型”，求事 件 M 发生的概率. 【答案】（1） 5 6 ；（2） 3 5 . 【解析】 （1）由题意知 30 人中一天走路步数超过 5000 步的有 25 人，频率为 5 6 ， 估计小李所有微信好友中每日走路步数超过 5000 步的概率为 5 6 . （2）5 人中“积极型”有 125 230   人，这两人分别记为 1 2,A A 5 人中“懈怠型”有 185 330   人，这三人分别记为 1 2 3, ,B B B . 在这 5 人中任选 2 人，共有以下 10 种不同的等可能结果：                    1 2 1 1 1 2 1 3 2 1 2 2 2 3 1 2 1 3 2 3, , , , , , , , , , , , , , , , , , ,A A A B A B A B A B A B A B B B B B B B . 事件 M “抽取的 2 人来自不同的类型”有以下 6 种不同的等可能结果：            1 1 1 2 1 3 2 1 2 2 2 3, , , , , , , , , . ,A B A B A B A B A B A B . 易得，其概率为 6 3 10 5  . 事件 M 发生的概率 3 5 . 21．某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为 120 件，60 件，30 件.为了解 它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为 n 的样本进行调查， 其中从乙车间的产品中抽取了 2 件。 （Ⅰ）应从甲、丙两个车间的产品中分别抽取多少件，样本容量 n 为多少？ （Ⅱ）设抽出的 n 件产品分别用 1A ， 2A ，…， nA 表示，现从中随机抽取 2 件产品。 （i）试用所给字母列举出所有可能的抽取结果； （ii）设 M 为事件“抽取的 2 件产品来自不同车间”，求事件 M 发生的概率. 【答案】（Ⅰ）答案见解析；（Ⅱ）（i）答案见解析；（ii） 2 3 . 【解析】 （Ⅰ）解：由已知甲、乙、丙三个车间抽取产品的数量之比是 4：2：1，由于采用分层抽样的 方法乙车间的产品中抽取了 2 件产品，因此应从甲、丙两个车间分别抽取 4 件和 1 件，样本 容量 n 为 7. （Ⅱ）（i）解：从抽出的 7 件产品中随机抽取两间产品的所有可能结果为  1 2,A A ， 1 3,A A ， 1 4,A A ， 1 5,A A ， 1 6,A A ， 1 7,A A ， 2 3,A A ， 2 4,A A ，  2 5,A A ， 2 6,A A ， 2 7,A A ， 3 4,A A ， 3 5,A A ， 3 6,A A ， 3 7,A A ， 4 5,A A ，  4 6,A A ， 4 7,A A ， 5 6,A A ， 5 7,A A ， 6 7,A A 共 21 种. （ii）解：不妨设抽出的 7 件产品中，来自甲车间的是 1A ， 2A ， 3A ， 4A ，来自乙车间的是 5A ， 6A ，来自丙车间的是 7A ，则从 7 件产品中抽取的 2 件产品来自不同车间的所有可能结果为  1 5,A A ， 1 6,A A ， 1 7,A A ， 2 5,A A ， 2 6,A A ， 2 7,A A ， 3 5,A A ，  3 6,A A ， 3 7,A A ， 4 5,A A ， 4 6,A A ， 4 7,A A ， 5 7,A A ， 6 7,A A ，共 14 种. 所以，事件发生的概率为   14 2 21 3P M   22．某医院治疗白血病有甲、乙两套方案，现就 70 名患者治疗后复发的情况进行了统计，得 到其等高条形图如图所示（其中采用甲、乙两种治疗方案的患者人数之比为5: 2) ． （1）补充完整 2 2 列联表中的数据，并判断是否有99% 把握认为甲乙两套治疗方案对患者 白血病复发有影响； 复发 未复发 总计 甲方案 乙方案 2 总计 70 （2）为改进“甲方案”，按分层抽样组成了由 5 名患者构成的样本，求随机抽取 2 名患者恰好 是复发患者和未复发患者各 1 名的概率． 附： 2 0( )P K k… 0.05 0.01 0.005 0.001 0k 3.841 6.635 7.879 10.828 n a b c d    ， 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d      ． 【答案】（1）见解析；（2） 3 5P  【解析】 （1）根据题意知，70 名患者中采用甲种治疗方案的患者人数为 50 人，采用乙种治疗方案的 患者人数为 20 人， 补充完整 2 2 列联表中的数据，如图所示； 复发 未复发 总计 甲方案 20 30 50 乙方案 2 18 20 总计 22 48 70 计算观测值得， 2 2 70 (20 18 30 2) 5.966 6.63522 48 50 20K         ， 所以没有 99% 的把握认为甲、乙两套治疗方案对患者白血病复发有影响； （2）在甲种治疗方案中按分层抽样抽取 5 名患者，复发的抽取 2 人，即为 A 、 B ； 未复发的抽取 3 人，记为 c 、 d 、 e ，从这 5 人中随机抽取 2 人，基本事件为： AB 、 Ac 、 Ad 、 Ae 、 Bc 、 Bd 、 Be 、 cd 、 ce 、 de 共 10 种， 其中 2 人恰好是复发患者和未复发患者各 1 名的基本事件为： Ac 、 Ad 、 Ae 、 Bc 、 Bd 、 Be 共 6 种， 则所求的概率为 6 3=10 5P  ．