2020_2021学年新教材高中数学第六章平面向量及其应用6 25页

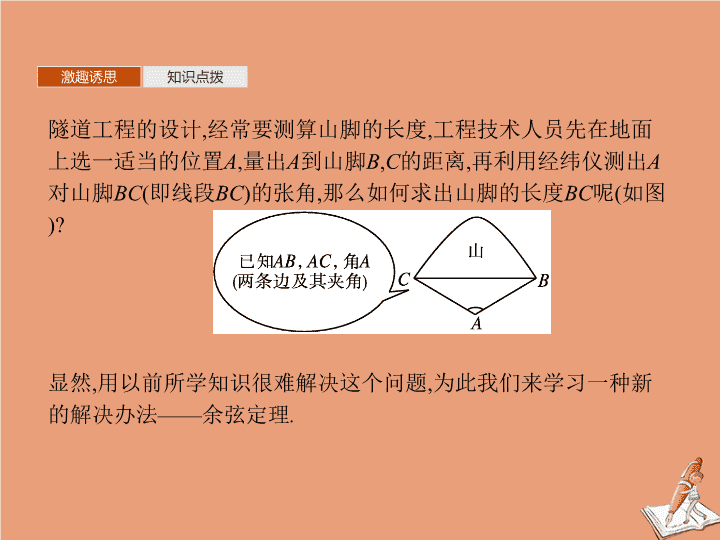
第 1 课时　余弦定理 课标阐释 思维脉络 1 . 掌握余弦定理及其变形 . ( 数学抽象 ) 2 . 掌握余弦定理的证明过程 . ( 逻辑推理 ) 3 . 能够利用余弦定理解决有关问题 . ( 数学运算 ) 激趣诱思 知识点拨 隧道工程的设计 , 经常要测算山脚的长度 , 工程技术人员先在地面上选一适当的位置 A , 量出 A 到山脚 B , C 的距离 , 再利用经纬仪测出 A 对山脚 BC ( 即线段 BC ) 的张角 , 那么如何求出山脚的长度 BC 呢 ( 如图 )? 显然 , 用以前所学知识很难解决这个问题 , 为此我们来学习一种新的解决办法 —— 余弦定理 . 激趣诱思 知识点拨 知识点一、余弦定理 1 . 文字语言 : 三角形中任何一边的平方 , 等于其他两边平方的和 减去 这两边与它们夹角的 余弦的积 的两倍 . 2 . 符号语言 : 在 △ ABC 中 , a 2 = b 2 +c 2 - 2 bc cos A , b 2 = c 2 +a 2 - 2 ca cos B , c 2 = a 2 +b 2 - 2 ab cos C . 名师点析 应用余弦定理解三角形的类型 (1) 已知两边及其夹角求第三边及其他两角 . (2) 已知三边求三角 . 激趣诱思 知识点拨 微练习 (1) 在 △ ABC 中 , 若 AB= 1, AC= 3, A= 60°, 则 BC= 　　　 .  (2) 已知 △ ABC 是等腰三角形 , 且 a=c= 5, B = 120°, 则 b= 　　　 .  激趣诱思 知识点拨 知识点二、余弦定理的推论 2 . 一般地 , 三角形的三个角 A , B , C 和它们的对边 a , b , c 叫做三角形的元素 . 已知三角形的几个元素求其他元素的过程叫做解三角形 . 激趣诱思 知识点拨 微 练习 探究一 探究二 探究三 素养形成 当堂检测 已知两边及一角解三角形 例 1 (1) 在 △ ABC 中 , 已知 b= 3, c= 2 , A= 30 °, 求 a ; (2) 在 △ ABC 中 , 已知 b= 3, c= 3 , B= 30 °, 求角 A 、角 C 和边 a. 分析 (1) 已知两边及其夹角 , 可直接利用余弦定理求出第三条边 . (2) 已知两边及一边的对角 , 可利用余弦定理列方程求解 . 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 已知三角形的两边及一角解三角形的方法 已知三角形的两边及一角解三角形 , 必须先判断该角是给出两边中一边的对角 , 还是给出两边的夹角 . 若是给出两边的夹角 , 可以由余弦定理求第三边 ; 若是给出两边中一边的对角 , 可以利用余弦定理建立一元二次方程 , 解方程求出第三边 . 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 已知三边解三角形 例 2 (1) 在 △ ABC 中 , 若 a 2 +b 2 +ab=c 2 , 则角 C= 　　　 ;  分析 (1) 根据已知条件结合余弦定理的变形求解 . (2) 先由三边的比值设出三边的长度 , 再利用余弦定理的变形求解 . 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 已知三角形的三边解三角形的方法 (1) 先利用余弦定理求出一个角的余弦值 , 从而求出第一个角 ; 再利用余弦定理求出第二个角 ; 最后利用三角形的内角和定理求出第三个角 ; (2) 利用余弦定理求出三个角的余弦值 , 进而求出三个角 . 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 利用余弦定理判断三角形形状 例 3 (1) 在 △ ABC 中 ,( a+b+c )( a+b-c ) = 3 ab 且 2cos A sin B= sin C , 试判断三角形的形状 ; (2) 在 △ ABC 中 , 若 a cos B+a cos C=b+c , 试判断该三角形的形状 . 分析 (1) 利用余弦定理及已知求出角 C , 再由三角恒等变换确定角 A 与角 B 的关系 , 进而判断三角形形状 . (2) 利用余弦定理将角转化为边 , 通过代数变形判断三角形的形状 . 探究一 探究二 探究三 素养形成 当堂检测 解 : (1) ∵ A+B+C= 180°, ∴ sin C= sin( A+B ) . ∵ 2cos A sin B= sin C , ∴ 2cos A sin B= sin A cos B+ cos A sin B , ∴ sin A cos B- cos A sin B= 0, ∴ sin( A-B ) = 0 . ∵ 0° c 2 , 且 b 2 +c 2 >a 2 , 且 c 2 +a 2 >b 2 . ③△ ABC 为钝角三角形 ⇔ a 2 +b 2