高中数学必修3教案：1_1_2-1_1_3程序框图与算法的基本逻辑结构(一、二) 2页

‎1.1.2‎‎ 程序框图（一） 教学要求：掌握程序框图的概念；会用通用的图形符号表示算法，掌握算法的三个基本逻辑结构. 掌握画程序框图的基本规则，能正确画出程序框图. 通过模仿、操作、探索，经历通过设计程序框图表达解决问题的过程；学会灵活、正确地画程序框图. 教学重点：程序框图的基本概念、基本图形符号和3种基本逻辑结构. 教学难点：综合运用框图知识正确地画出程序框图 教学过程： 一、复习准备： ‎1. 写出算法：给定一个正整数n，判定n是否偶数. ‎2. 用二分法设计一个求方程的近似根的算法. 二、讲授新课： ‎1. 教学程序框图的认识： ‎① 讨论：如何形象直观的表示算法？ →图形方法. 教师给出一个流程图（上面1题），学生说说理解的算法步骤. ‎② 定义程序框图：程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形. ‎③基本的程序框和它们各自表示的功能：‎ 程序框 名称 功能 终端框 ‎（起止框）‎ 表示一个算法的起始和结束 输入、输出框 表示一个算法输入和输出的信息 处理（执行）框 赋值、计算 判断框 判断一个条件是否成立 流程线 连接程序框 ‎④ 阅读教材P5的程序框图. → 讨论：输入35后，框图的运行流程，讨论：最大的I值. ‎2. 教学算法的基本逻辑结构： ① 讨论：P5的程序框图，感觉上可以如何大致分块？流程再现出一些什么结构特征？ ‎→ 教师指出：顺序结构、条件结构、循环结构. ‎② 试用一般的框图表示三种逻辑结构. （见下图） ‎ ‎③ 出示例3：已知一个三角形的三边分别为4,5,6，利用海伦公式设计一个算法，求出它的面积，并画出算法的程序框图. （学生用自然语言表示算法→师生共写程序框图→讨论：结构特征） ‎④ 出示例4：任意给定3个正实数，设计一个算法，判断分别以这3个数为三边边长的三角形是否存在.画出这个算法的程序框图. (学生分析算法→写出程序框图→试验结果→讨论结构) ‎⑤ 出示例5：设计一个计算1＋2＋3＋…＋1000的值的算法，并画出程序框图. ‎ (学生分析算法→写出程序框图→给出另一种循环结构的框图→对比两种循环结构) ‎3. 小结：程序框图的基本知识；三种基本逻辑结构；画程序框图要注意：流程线的前头；判断框后边的流程线应根据情况标注“是”或“否”；循环结构中要设计合理的计数或累加变量等. 三、巩固练习： 1.练习：把复习准备题②的算法写成框图. 2. 作业：P‎12 A组 1、2题. ‎1.1.2‎‎ 程序框图（二） 教学要求：更进一步理解算法，掌握算法的三个基本逻辑结构. 掌握画程序框图的基本规则，能正确画出程序框图.学会灵活、正确地画程序框图. 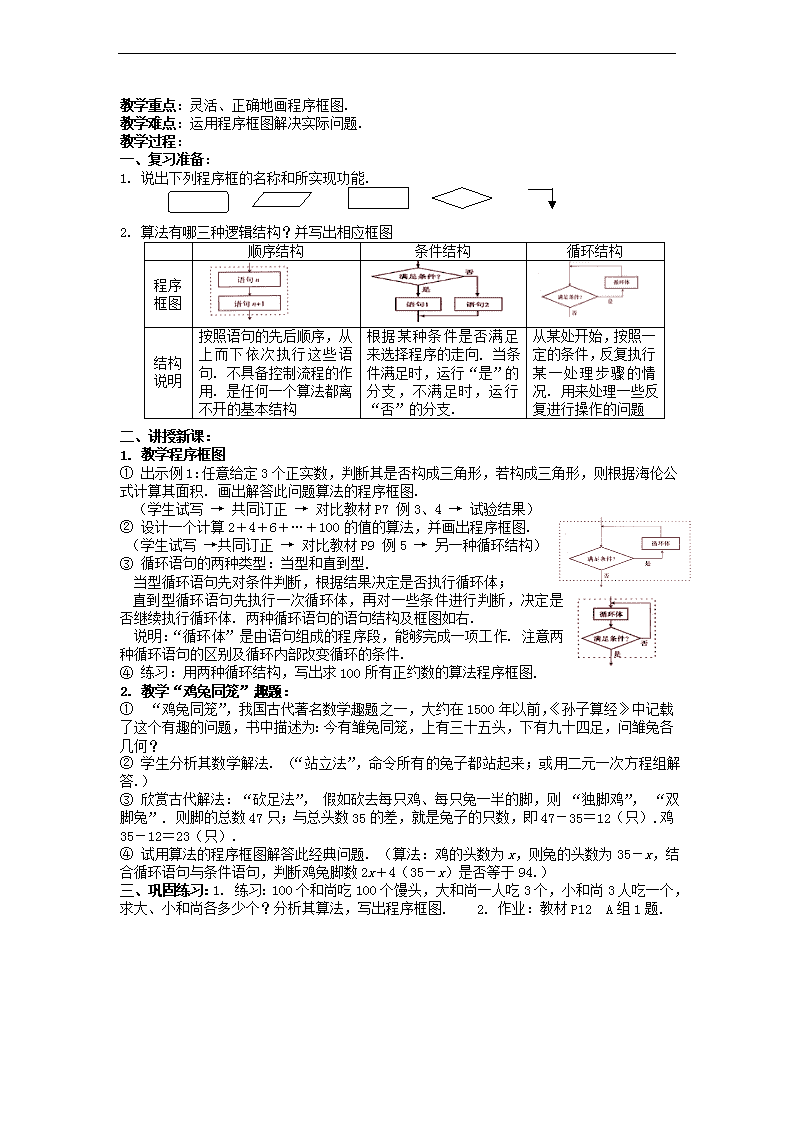教学重点：灵活、正确地画程序框图.‎ 教学难点：运用程序框图解决实际问题.‎ 教学过程：‎ 一、复习准备：‎ ‎1. 说出下列程序框的名称和所实现功能.‎ ‎2. 算法有哪三种逻辑结构？并写出相应框图 顺序结构 条件结构 循环结构 程序 框图 结构 说明 按照语句的先后顺序，从上而下依次执行这些语句. 不具备控制流程的作用. 是任何一个算法都离不开的基本结构 根据某种条件是否满足来选择程序的走向. 当条件满足时，运行“是”的分支，不满足时，运行“否”的分支.‎ 从某处开始，按照一定的条件，反复执行某一处理步骤的情况. 用来处理一些反复进行操作的问题 ‎ ‎ 二、讲授新课：‎ ‎1. 教学程序框图 ‎① 出示例1：任意给定3个正实数，判断其是否构成三角形，若构成三角形，则根据海伦公式计算其面积. 画出解答此问题算法的程序框图.‎ ‎ （学生试写 → 共同订正 → 对比教材P7 例3、4 → 试验结果）‎ ‎② 设计一个计算2＋4＋6＋…＋100的值的算法，并画出程序框图.‎ ‎ （学生试写 →共同订正 → 对比教材P9 例5 → 另一种循环结构）‎ ‎③ 循环语句的两种类型：当型和直到型. ‎ 当型循环语句先对条件判断，根据结果决定是否执行循环体；‎ 直到型循环语句先执行一次循环体，再对一些条件进行判断，决定是否继续执行循环体. 两种循环语句的语句结构及框图如右.‎ 说明：“循环体”是由语句组成的程序段，能够完成一项工作. 注意两种循环语句的区别及循环内部改变循环的条件.‎ ‎④ 练习：用两种循环结构，写出求100所有正约数的算法程序框图.‎ ‎2. 教学“鸡兔同笼”趣题：‎ ① ‎“鸡兔同笼”，我国古代著名数学趣题之一，大约在1500年以前，《孙子算经》中记载了这个有趣的问题，书中描述为：今有雏兔同笼，上有三十五头，下有九十四足，问雏兔各几何？‎ ‎② 学生分析其数学解法. （“站立法”，命令所有的兔子都站起来；或用二元一次方程组解答.）‎ ‎③ 欣赏古代解法：“砍足法”， 假如砍去每只鸡、每只兔一半的脚，则 “独脚鸡”， “双脚兔”. 则脚的总数47只；与总头数35的差，就是兔子的只数，即47－35＝12（只）.鸡35－12＝23（只）.‎ ‎④ 试用算法的程序框图解答此经典问题. （算法：鸡的头数为x，则兔的头数为35－x，结合循环语句与条件语句，判断鸡兔脚数2x＋4（35－x）是否等于94.）‎ 三、巩固练习：1. 练习：100个和尚吃100个馒头，大和尚一人吃3个，小和尚3人吃一个，求大、小和尚各多少个？分析其算法，写出程序框图. 2. 作业：教材P‎12 A组1题. ‎