2021届高考数学一轮复习第九章平面解析几何第8节曲线与方程课件新人教A版 25页

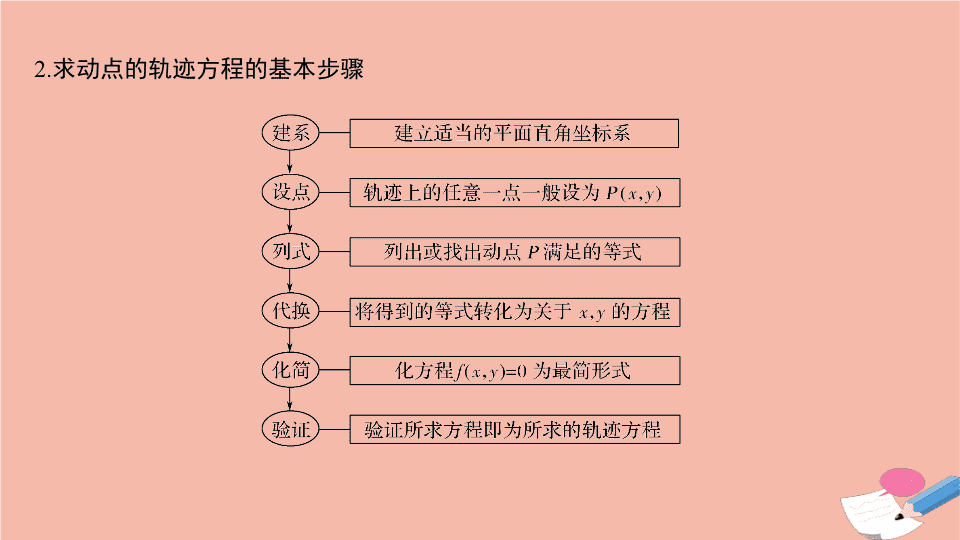
第 8 节　曲线与方程 考试要求　 1. 了解方程的曲线与曲线的方程的对应关系； 2. 了解解析几何的基本思想和利用坐标法研究曲线的简单性质； 3. 能够根据所给条件选择适当的方法求曲线的轨迹方程 . 知 识 梳 理 1. 曲线与方程的定义 一般地，在直角坐标系中，如果某曲线 C 上的点与一个二元方程 f ( x ， y ) ＝ 0 的实数解建立如下的对应关系： 那么，这个方程叫做 ______________ ，这条曲线叫做 ______________ . 这个方程的解 曲线上的点 曲线的方程 方程的曲线 2. 求动点的轨迹方程的基本步骤 [ 常用结论与微点提醒 ] 1. “ 曲线 C 是方程 f ( x ， y ) ＝ 0 的曲线 ” 是 “ 曲线 C 上的点的坐标都是方程 f ( x ， y ) ＝ 0 的解 ” 的充分不必要条件 . 2. 曲线的交点与方程组的关系： (1) 两条曲线交点的坐标是两个曲线方程的公共解，即两个曲线方程组成的方程组的实数解； (2) 方程组有几组解，两条曲线就有几个交点；方程组无解，两条曲线就没有交点 . 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) 答案　 (1) √ 　 (2) × 　 (3) × 　 (4) × 2. ( 老教材选修 2 － 1P37A2 改编 ) 已知 M ( － 1 ， 0) ， N (1 ， 0) ， | PM | － | PN | ＝ 2 ，则动点 P 的轨迹是 ( 　　 ) A. 双曲线 B. 双曲线左支 C. 一条射线 D. 双曲线右支 解析　 由于 | PM | － | PN | ＝ | MN | ，所以 A ， B ， D 不正确，应为以 N 为端点，沿 x 轴正向的一条射线 . 答案　 C 3. ( 老教材选修 2 － 1P37A1 改编 ) 已知 A ( － 2 ， 0) ， B (1 ， 0) 两点，动点 P 不在 x 轴上，且满足 ∠ APO ＝ ∠ BPO ，其中 O 为原点，则点 P 的轨迹方程是 ________. 答案　 ( x － 2) 2 ＋ y 2 ＝ 4( y ≠ 0) A. 两条直线 B. 两条射线 C. 两条线段 D. 一条直线和一条射线 答案　 D A. 双曲线 B. 椭圆 C. 圆 D. 抛物线 解析　 由已知 | MF | ＝ | MB | ，根据抛物线的定义知，点 M 的轨迹是以点 F 为焦点，直线 l 为准线的抛物线 . 答案　 D 6. 已知点 P 在曲线 2 x 2 － y ＝ 0 上移动，则点 A (0 ，－ 1) 与点 P 连线的中点的轨迹方程是 ________________. 考点一　直接法求轨迹方程 规律方法　 利用直接法求轨迹方程 (1) 利用直接法求解轨迹方程的关键是根据条件准确列出方程，然后进行化简 . (2) 运用直接法应注意的问题： ① 在用直接法求轨迹方程时，在化简的过程中，有时破坏了方程的同解性，此时就要补上遗漏的点或删除多余的点，这是不能忽视的； ② 若方程的化简过程是恒等变形，则最后的验证可以省略 . 【训练 1 】 与 y 轴相切并与圆 C ： x 2 ＋ y 2 － 6 x ＝ 0 也外切的圆的圆心的轨迹方程为 ________. 答案　 y 2 ＝ 12 x ( x >0) 或 y ＝ 0( x <0) 考点二　定义法求轨迹方程　 典例迁移 【例 2 】 ( 经典母题 ) 已知圆 M ： ( x ＋ 1) 2 ＋ y 2 ＝ 1 ，圆 N ： ( x － 1) 2 ＋ y 2 ＝ 9 ，动圆 P 与圆 M 外切并且与圆 N 内切，圆心 P 的轨迹为曲线 C . 求 C 的方程 . 解　 由已知得圆 M 的圆心为 M ( － 1 ， 0) ，半径 r 1 ＝ 1 ；圆 N 的圆心为 N (1 ， 0) ，半径 r 2 ＝ 3. 设圆 P 的圆心为 P ( x ， y ) ，半径为 R . 因为圆 P 与圆 M 外切并且与圆 N 内切， 所以 | PM | ＋ | PN | ＝ ( R ＋ r 1 ) ＋ ( r 2 － R ) ＝ r 1 ＋ r 2 ＝ 4 ＞ | MN | ＝ 2. 【迁移 1 】 将本例的条件 “ 动圆 P 与圆 M 外切并且与圆 N 内切 ” 改为 “ 动圆 P 与圆 M 、圆 N 都外切 ” ，则圆心 P 的轨迹方程为 ________. 解析　 由已知得圆 M 的圆心为 M ( － 1 ， 0) ，半径 r 1 ＝ 1 ；圆 N 的圆心为 N (1 ， 0) ，半径 r 2 ＝ 3. 设圆 P 的圆心为 P ( x ， y ) ，半径为 R ，因为圆 P 与圆 M ， N 都外切，所以 | PM | － | PN | ＝ ( R ＋ r 1 ) － ( R ＋ r 2 ) ＝ r 1 － r 2 ＝－ 2 ，即 | PN | － | PM | ＝ 2 ，又 | MN | ＝ 2 ，所以点 P 的轨迹方程为 y ＝ 0( x < － 2). 答案　 y ＝ 0( x < － 2) 【迁移 2 】 在本例中，若动圆 P 过圆 N 的圆心，并且与直线 x ＝－ 1 相切，则圆心 P 的轨迹方程为 ________. 解析　 由于点 P 到定点 N (1 ， 0) 和定直线 x ＝－ 1 的距离相等，所以根据抛物线的定义可知，点 P 的轨迹是以 N (1 ， 0) 为焦点，以 x 轴为对称轴、开口向右的抛物线，故其方程为 y 2 ＝ 4 x . 答案　 y 2 ＝ 4 x 规律方法　 定义法求曲线方程的两种策略 (1) 运用圆锥曲线的定义求轨迹方程，可从曲线定义出发直接写出方程，或从曲线定义出发建立关系式，从而求出方程 . (2) 定义法和待定系数法适用于已知曲线的轨迹类型，利用条件把待定系数求出来，使问题得解 . 【训练 2 】 (2020· 豫北名校联盟联考 ) 已知 △ ABC 中， AB ＝ 2 ，且 sin A (1 － 2cos B ) ＋ sin B (1 － 2cos A ) ＝ 0 ，以边 AB 的中垂线为 x 轴，以 AB 所在的直线为 y 轴，建立平面直角坐标系，则动点 C 的轨迹方程为 ________. 考点三　相关点 ( 代入 ) 法求轨迹方程 【例 3 】 (1)( 2020· 银川模拟 ) 动点 A 在圆 x 2 ＋ y 2 ＝ 1 上移动时，它与定点 B (3 ， 0) 连线的中点的轨迹方程是 ________. 解析　 (1) 设中点 M ( x ， y ) ，由中点坐标公式，可得 A (2 x － 3 ， 2 y ) ，因为点 A 在圆上，将点 A 的坐标代入圆的方程，所以轨迹方程为 (2 x － 3) 2 ＋ 4 y 2 ＝ 1. 答案　 (1)(2 x － 3) 2 ＋ 4 y 2 ＝ 1 　 (2) y 2 ＝ 4 x