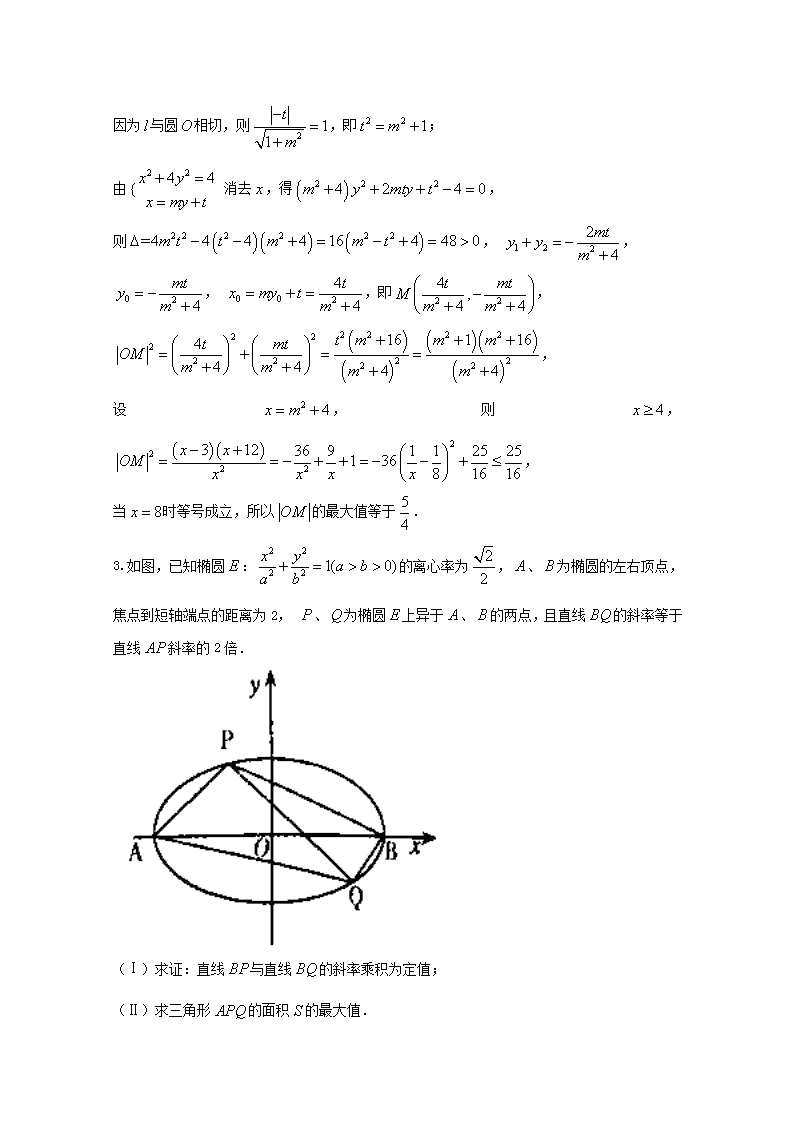高考数学命题角度5_4圆锥曲线的最值范围问题大题狂练理 18页

命题角度 5.4：圆锥曲线的最值范围问题 1. 已知椭圆 2 2 2 2: 1( 0)x yC a ba b     的离心率为 3 2 ，短轴长为 2. （1）求椭圆C 的标准方程； （2）设直线 :l y kx m  与椭圆 C 交于 ,M N 两点， O 为坐标原点，若 5 4OM ONk k  ，求 原点O 到直线l 的距离的取值范围. 【答案】（1） 2 2 14 x y  ；（2） 2 140, 7       （2）设  1 1,M x y ，  2 2,N x y ，联立 2 2{ 14 y kx m x y     得  2 2 24 1 8 4 4 0k x kmx m     ， 依 题 意 ，     2 2 28 4 4 1 4 4 0km k m     ， 化 简 得 2 24 1m k  ， ① ， 1 2 2 8 4 1 kmx x k     ， 2 1 2 2 4 4 4 1 mx x k   ，     2 2 1 2 1 2 1 2 1 2y y kx m kx m k x x km x x m       ，若 5 4OM ONk k  ，则 1 2 1 2 5 4 y y x x  ， 即 1 2 1 24 5y y x x ， ∴  2 2 1 2 1 2 1 24 4 4 5k x x km x x m x x    ， ∴    2 2 2 2 2 4 1 84 5 4 4 04 1 4 1 m kmk km mk k            ， 即     2 2 2 2 2 24 5 1 8 4 1 0k m k m m k    ﹣ ，化简得 2 2 5 4m k  ，②，由①②得 2 60 5m  ， 21 5 20 4k  ， ∵ 原 点 O 到 直 线 l 的 距 离 21 md k   ， ∴   2 2 2 2 2 2 5 94 11 1 4 1 kmd k k k         ，又∵ 21 5 20 4k  ，∴ 2 80 7d  ，∴原点 O 到直 线l 的距离的取值范围是 2 140, 7      2.已知椭圆 2 2 2 2: 1( 0)x yC a ba b     的离心率为 3 2 ，短轴长为 2 ． （Ⅰ）求椭圆 C 的标准方程； （Ⅱ）若圆 2 2: 1O x y  的切线 l 与曲线 E 相交于 A 、 B 两点，线段 AB 的中点为 M ，求 OM 的最大值． 【答案】（Ⅰ）C 的标准方程 2 2 14 x y  （Ⅱ） OM 的最大值等于 5 4 【解析】试题分析:(1)待定系数法求椭圆方程;(2)借助韦达定理表示 OM 的最大值,利用二 次函数求最值. 试题解析: （I） 2 2b  ，所以 1b  ,又 2 2 3 2 a b a   ，解得 2a  ． 所以椭圆 C 的标准方程 2 2 14 x y  ． （II）设  1 1,A x y ，  2 2,B x y ，  0 0,M x y ，易知直线l 的斜率不为0 ，则设 :l x my t  ． 因为l 与圆O 相切，则 2 1 1 t m    ，即 2 2 1t m  ； 由 2 24 4{ x y x my t     消去 x ，得  2 2 24 2 4 0m y mty t     ， 则     2 2 2 2 2 2=4 4 4 4 16 4 48 0m t t m m t         ， 1 2 2 2 4 mty y m     ， 0 2 4 mty m    ， 0 0 2 4 4 tx my t m     ，即 2 2 4 ,4 4 t mtM m m      ，          2 2 2 22 2 2 2 22 2 2 2 16 1 164 4 4 4 4 t m m mt mtOM m m m m                   ， 设 2 4x m  ， 则 4x  ，    2 2 2 2 3 12 36 9 1 1 25 251 36 8 16 16 x xOM x x x x                ， 当 8x  时等号成立，所以 OM 的最大值等于 5 4 ． 3. 如图，已知椭圆 E ： 2 2 2 2 1( 0)x y a ba b     的离心率为 2 2 ， A 、 B 为椭圆的左右顶 点，焦点到短轴端点的距离为 2， P 、Q 为椭圆 E 上异于 A 、B 的两点，且直线 BQ 的斜率 等于直线 AP 斜率的 2 倍． （Ⅰ）求证：直线 BP 与直线 BQ 的斜率乘积为定值； （Ⅱ）求三角形 APQ 的面积 S 的最大值． 【答案】（Ⅰ）见解析;（Ⅱ） 32 9 . 【解析】试题分析：（Ⅰ）由椭圆的方程可得点 P,A,B 的坐标，利用两点式求直线斜率的方法 可 求 出 BP,BQ 的 斜 率 乘 积 为 定 值 -1 ；（ Ⅱ ） 当 直 线 PQ 的 斜 率 存 在 时 ， 216 7 149 2 2APQS t t       ， 20 1t t   ， 32 9APQS  ，当直线 PQl 的斜率 k 不存在时， 1 8 8 32 2 3 3 9APQS     ，故综合 ΔAPQS 的最大值为 32 9 . 试题解析： （Ⅰ） 2 2 14 2 x y  ． 1 2AP BPk k   ，故 1BP BQk k   ． 2y kx k  或 2 3y kx k  ，所以过定点 2,0 或 2 ,03      ， 点 2,0 为右端点，舍去， 1 2 1 2APQ APM AQMS S S OM y y                2 2 2 2 2 2 22 2 8 2 4 16 98 16 3 92 1 2 1 k k b k k k k         22 2 16 7 1 149 2 2 1 2 2 1k k          ， 令 2 1 2 1 tk  （ 0 1t  ）， 216 7 149 2 2APQS t t       ， 20 1t t   ， 32 9APQS  ， 当直线 PQl 的斜率 k 不存在时，  1 1,P x y ，  1 1,Q x y ， 1 2AP BQk k ，即 1 1 1 1 2 2 2 y y x x   ，解得 1 2 3x  ， 1 4 3y  ， 1 8 8 32 2 3 3 9APQS     ， 所以 APQS 的最大值为 32 9 . 4 已知椭圆 :E 2 2 2 2 1( 0)x y a ba b     的左、右焦点分别为 1F 、 2F ， A 为椭圆 E 的右顶点， B ， C 分别为椭圆 E 的上、下顶点.线段 2CF 的延长线与线段 AB 交于点 M ，与椭圆 E 交 于点 P .（1）若椭圆的离心率为 2 2 ， 1PFC 的面积为 12，求椭圆 E 的方程；（2）设 2 1ΔS CMF CPFS  ，求实数  的最小值. 【答案】（1） 2 2 118 9 x y  （2） 2 2 2 试题解析：解：（1） 1 2FCF 是等腰直角三角形，由勾股定理知， 2 2 2 1 1| | | |PF CF CP    22 2 1 2| |PF a a PF     22 2 1 1| | 3PF a a PF   解得， 1 5a 3PF  ， 2 3 aPF  ， 4 3 aPC  ， 则 1 1 4 122 3PF C aS a    ，即 2 18a  ， 2 9b  . 所以椭圆 E 的方程为 2 2 118 9 x y  . （2）设  ,P x y ，因为直线 AB 的方程为 by x ba    ，直线 PC 的方程为 by x ba    ， 所以联立方程解得 2 ,ac ab bcM a c a c       . 因为 1 1CMF CPFS S   ，所以 CM CP ，所以CM CP   ， 所以  2 , ,ac ab bc x y ba c a c        ，所以   2acx a c  ，  2ab b a cy a c    ， 代入椭圆 E 的方程，得       22 2 22 2 24 1 a a cc a c a c           ， 即   224 2c a a c       22 a c  ， 所以   2 2 21 1 a c e a a c e        2 21 2 2 1 21 1e ee e         =2 2 2 ， 因为 0 1e  所以1 1 2e   ，所以当且仅当 1 2e   即 2 1e   时，  取到最小值 2 2 2 . 5.已知点 M 是圆心为 E 的圆 2 23 16x y   上的动点，点  3,0F ，线段 MF 的垂直 平分线交 EM 于点 P . （1）求动点 P 的轨迹C 的方程； （2）矩形 ABCD 的边所在直线与曲线C 均相切，设矩形 ABCD 的面积为 S ，求 S 的取值范 围. 【答案】(1) 2 2 14 x y  ;(2) 8 10S  . 【解析】试题分析：（1）利用定义法求椭圆的轨迹方程；（2）设 AB 的方程为 1y k x m  ， CD 的方程为 1y k x m  ，直线 AB 与 CD 间的距离为 1 2 1 2 1 md k   ，直线 BC 与 AD 间的 距离为 2 2 2 2 1 nd k   ， 2 2 21 2 1 2 2 2 2 94 4 11 1 2 m nS k k k k             ，从而得到 S 的范围. (2)①当矩形的边与坐标轴垂直或平行时，易得 8S  ； ②当矩形的边均不与坐标轴垂直或平行时，其四边所在直线的斜率存在且不为 0， 设 AB 的方程为 1y k x m  ， BC 的方程为 2y k x n  ，则 CD 的方程为 1y k x m  ， AD 的方程为 2y k x n  ，其中 1 2 1k k   ， 直线 AB 与 CD 间的距离为   1 2 2 1 1 2 1 1 m m md k k       ， 同理直线 BC 与 AD 间的距离为   2 2 2 2 2 2 1 1 n n nd k k       ， 所以  1 2 2 2 1 2 2 2 * 1 1 m nS d d k k        2 2 2 2 2 1 1 1 1 1{ 2 1 04 4 x y k x k mx m y k x m             ， 因 为 直 线 AB 与 椭 圆 相 切 ， 所 以 2 2 14 1 0k m     ， 所 以 2 14 1m k  ， 同 理 2 24 1n k  ， 所以     2 2 2 22 2 1 2 1 21 2 2 2 2 2 2 2 1 2 1 2 1 2 4 16 4 14 4 1 4 1 1 1 1 k k k kk kS k k k k k k               2 2 1 2 2 2 1 2 4 17 4 2 k k k k       2 2 21 2 1 2 2 9 94 4 4 4 2 12k k k k               ， 2 1 2 1 1 2k k   (当且仅当 1 1k   时，不等式取等号）， 所以 94 4 4 42 2S    ，即8 10S  ， 由①②可知， 8 10S  . 6.已知椭圆 2 2 2 2: 1x yC a b   （ 0a b  ）的右焦点为 F ，过椭圆 C 中心的弦 PQ 长为 2，且 090PFQ  ， PQF 的面积为 1. （1）求椭圆C 的方程； （2）设 1 2,A A 分别为椭圆C 的左、右顶点， S 为直线 2 2x  上一动点，直线 1A S 交椭圆C 于点 M ，直线 2A S 交椭圆于点 N ，设 1 2,S S 分别为 1 2A SA ， MSN 的面积，求 1 2 S S 的最大 值. 【答案】（1） 2 2 12 x y  （2）见解析 【解析】试题分析： (1)由题意求得 1, 1c b  ，则椭圆方程为 2 2 12 x y  ； (2) 由 题 意 求 得 面 积 比 值 的 解 析 式       1 2 22 2 2 2 A SA 1 2 22 2 2MSN t 9 3t 3 2S SA ·SA t 9 t 1 1 4· ·S SM·SN t 3 t 3 3 3t 3                   ， 当 且 仅 当 2 29 3 3t t   ，即 3t   时取“ ”. 试题解析： 解： （2）设直线 1 3 2: 2A S x yt   ，代入 2 22 2x y  中， 得 2 2 18 122 0y yt t       ，解得 1 2 6 9 ty t   同理，设直线 2 2: 2A S x yt   ，带入 2 22 2x y  中， 得 2 2 2 42 0y yt t       ，解得 2 2 2 1 ty t    1 2 2 2 1 2 2 2 · 9 1·· 3 3 A SA MSN S SA SA t t S SM SN t t              22 2 22 9 3 3 2 1 4·3 33 t t t            当且仅当 2 29 3 3t t   ，即 3t   时取“ ” 7. 已知圆 ，点 是圆 上任意一点，线段 的垂直平分线交 于点 ， 当点 在圆上运动时，点 的轨迹为曲线 ． （Ⅰ）求曲线 的方程； （Ⅱ）若直线 与曲线 相交于 两点， 为坐标原点，求 面积的最大值． 【答案】（Ⅰ） ;（Ⅱ） ． 【 解 析 】 试 题 分 析 ：（ 1 ） 由 垂 直 平 分 线 的 几 何 意 义 可 知 ， ，满足椭圆的定义。（2）直线 与椭圆组方程组， 由 韦 达 定 理 、 弦 长 公 式 和 点 到 直 线 的 距 离 公 式 ， 可 求 得 ．由 ，得 及均值不等式可求得 面积的最大 值． （Ⅱ）设 ． 联立 消去 ，得 ． 此时有 ． 由一元二次方程根与系数的关系，得 ， ． ∴ ． ∵原点 到直线 的距离 ， ∴ ． 由 ，得 ．又 ，∴据基本不等式，得 ． 当且仅当 时，不等式取等号． ∴ 面积的最大值为 ． 8.已知点  1,0F ，点 A 是直线 1 : 1l x   上的动点，过 A 作直线 2l ， 1 2l l ，线段 AF 的垂 直平分线与 2l 交于点 P ． (1)求点 P 的轨迹C 的方程； (2)若点 ,M N 是直线 1l 上两个不同的点，且 PMN 的内切圆方程为 2 2 =1x y ，直线 PF 的 斜率为 k ，求 k MN 的取值范围． 【答案】(1) 2 4y x ;(2) 10, 2      . 【解析】试题分析：（1）利用抛物线定义求解即可； （2）设出 PMN 的三个顶点的坐标，表示出 ,PM PN 的解析式，化简之后可得 ,m n 为关于 t 的方程   2 0 0 01 2 1 0x t y t x     的两根，然后由韦达定理表示 MN 的长度，最后在 PF 中消去参数 ,m n ，故可以得到 k MN 的取值范围. 试题解析： (1)据题设分析知，点 P 的轨迹 C 是以点  1,0F 为焦点，直线 1 : 1l x   为准线 的抛物线，所以曲线C 的方程为 2 4y x . (2)设  0 0,P x y ，点  1,M m ，点  1,N n ， 直线 PM 的方程为  0 0 11 y my m xx    ， 化简，得        0 0 0 01 1 0y m x x y y m m x        ， 又因为 PMN 内切圆的方程为 2 2 1x y  ． 所以圆心  0,0 到直线 PM 的距离为 1，即       0 0 2 2 0 0 1 1 1 y m m x y m x        ， 所以          2 2 2 22 0 0 0 0 0 0+ 1 2 1 1y m x y m m y m x m x         ， 由题意，得 0 1x  ，所以   2 0 0 01 2 1 0x m y m x     . 同理，有    2 0 0 01 2 1 0x n y n x     ， 所以 ,m n 是关于t 的方程    2 0 0 01 2 1 0x t y t x     的两根， 所以  00 0 0 12 ,1 1 xym n mnx x      因为 所以      2 2 00 2 00 4 14= 4 11 xyMN m n m n mn xx        . 因为 2 0 0 0 04 , 2y x y x  ， 所以       2 00 0 0 2 2 00 0 4 116 4 1= 211 1 xx x xMN xx x       . 直线 PF 的斜率 0 0 1 yk x   ，则 00 0 0 2=1 1 xyk x x    ， 所以 0 2 0 0 0 0 1 14 1 4 k x MN x x x x      . 因为函数 1y x x   在 1, 上单调递增，所以当 0 1x  时， 0 0 1 0x x   ， 所以 0 0 1 10 1 44x x     ，所以 0 0 1 10 1 24x x     ， 所以 10 2 k MN   .所以 k MN 的取值范围是 10, 2      . 9. 如下图，已知椭圆 2 2 2 2 1( 0)x y a ba b     的上顶点为 A ，左、右顶点为 B C、 ，右焦点为 F ， 3AF  ，且 ABC 的周长为 14. （I）求椭圆的离心率； （II）过点  4,0M 的直线 l 与椭圆相交于不同两点 P Q、 ，点 N 在线段 PQ 上．设 MP MQ PN QN    ，试判断点 N 是否在一条定直线上，并求实数λ的取值范围． 【答案】（Ⅰ） 2 3e  ；（Ⅱ） 4 ,3       . 试题解析： （I）由 2 2 2 2| |AF b c a   ，得 3a  ， ABC 的周长为  2 14AC a  ，即 2 2 7b a a   ，得 2 7b  ， 所以 2c  ，椭圆的离心率为 2 3e  ； （II）显然直线 l 的斜率存在，设 l 的方程为  4y k x  ， 设 P(x1，y1)，Q(x2，y2)，N(x0，y0)， 由 MP MQ PN QN  ，得 1 2 0 1 2 0 y y y y y y   ，化简得  1 2 0 1 22y y y y y  ①，-----6 分 由   2 2 4 , { 1.9 7 y k x x y     消去 x，得 2 2 29 7 56 49 0k y ky k    ， 得 1 2 2 56 9 7 ky y k     ， 2 1 2 2 49 9 7 ky y k   ， 代入①式得 0 7 4y k  ，由  0 0 4y k x  得 0 9 4x  ， 01 1 0 1 0 1 7 44 41 1 9 4 MP xx PN x x x x x            ， 因为 1 9 34 x  ，得 1 9 30 4 4x   ，所以 7 41 3 3      ， 因此，N 在一条直线 9 4x  上，实数 4 ,3       ． 【法二：显然直线 l 的斜率存在，设 l 的方程为  4y k x  ，不妨设 0k  ， 设 P(x1，y1)，Q(x2，y2)，N(x0，y0)， 2 1y y ， 由 MP MQ PN QN    ，得 1 2 0 1 2 0 y y y y y y     ，化简得  1 2 0 1 22y y y y y  ①，6 分 由  1 0 1y y y  ，  2 2 0y y y  ，得  1 2 2 1y y y y   ②， 由   2 2 4 , { 1.9 7 y k x x y     消去 x，得 2 2 29 7 56 49 0k y ky k    ， 可知      2 2 256 4 9 7 49k k k     2 249 36 1 0k k   ， 得 1 2 2 56 9 7 ky y k     ， 2 1 2 2 49 9 7 ky y k   ，  1,2 2 56 2 9 7 ky k     ， 代入①式得 0 7 4y k  ，由  0 0 4y k x  得 0 9 4x  ， 由②式得 2 56 9 7 k k   29 7k      ，得 2 2 56 4 4 342 1 3 1 k k k k       ， 因此，N 在一条直线 9 4x  上，实数 4 ,3       ． 法三：设 P(x1，y1)，Q(x2，y2)，N(x0，y0)， 2 1x x ，由 MP MQ PN QN    ， 得 , ,MP PN MQ QN       所以 0 1 0 1 0 2 0 2 4 1 1 4 1 1 xx yy xx yy                      ,将  1 1,A x y ，  2 2,B x y 代入椭圆方程得 上面两式相减化简得 0 9 4x  01 1 0 1 0 1 7 44 41 1 9 4 MP xx PN x x x x x             ， 因为 1 9 34 x  ，得 1 9 30 4 4x   ，所以 7 41 3 3      ， 因此，N 在一条直线 9 4x  上，实数 4 ,3       ． 点睛：本题主要考查直线与圆锥曲线位置关系，所使用方法为韦达定理法：因直线的方程是 一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最 终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一， 尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用． 10.平面直角坐标系 中，已知椭圆 ： 的离心率为 ，左、右焦 点分别是 . 以 为圆心以 3 为半径的圆与以 为圆心 1 为半径的圆相交，且交点在椭 圆 上. (Ⅰ)求椭圆 的方程； （Ⅱ ）设椭圆 为椭圆 上任意一点，过点 的直线 交椭 圆 于 两点，射线 交椭圆 于点 . ( i )求 的值； （ii）求△ 面积的最大值. 【答案】（I） 2 2 14 x y  ；（II）( i )2；（ii） 6 3 . （II）由（I）知椭圆 E 的方程为 2 2 116 4 x y  （i）设  0 0,P x y ， OQ OP  ，由题意知  0 0,Q x y   因为 2 20 0 14 x y  又    2 2 0 0 116 4 x y    ，即 22 20 0 14 4 x y       所以 2  ，即 2OQ OP  （ii）设    1 1 2 2, , ,A x y B x y 将 y kx m  代入椭圆 E 的方程， 可得 2 2 21 4 8 4 16 0k x kmx m     由 0  ，可得 2 24 16m k  …………………………① 则有 2 1 2 1 22 2 8 4 16,1 4 1 4 km mx x x xk k      所以 2 2 1 2 2 4 16 4 1 4 k mx x k     因为直线 y kx m  与轴交点的坐标为  0,m 所以 OAB 的面积 2 2 2 2 2 2 16 41 2 1 4 k m mS m x x k       2 2 2 2 2 2 2 2 2 (16 4 ) 2 41 4 1 4 1 4 k m m m m k k k            令 2 21 4 m tk  将 y kx m  代入椭圆 C 的方程 可得  2 2 21 4 8 4 4 0k x kmx m     由 0  ，可得 2 21 4m k  …………………………………………② 由①②可知 0 1t  因此   22 4 2 4S t t t t     故 2 3S  当且仅当 1t  ，即 2 21 4m k  时取得最大值 2 3 由（i）知， ABQ 面积为3S 所以 ABQ 面积的最大值为 6 3 .