高中数学人教a版选修4-1学业分层测评2平行线分线段成比例定理word版含解析 8页

学业分层测评(二) (建议用时：45 分钟) [学业达标] 一、选择题 1．如图 1216，梯形 ABCD 中，AD∥BC，E 是 DC 延长线上一点，AE 分 别交 BD 于 G，交 BC 于 F.下列结论：①EC CD ＝EF AF ；②FG AG ＝BG GD ；③AE AG ＝BD DG ；④ AF CD ＝AE DE.其中正确的个数是( ) 图 1216 A．1 B．2 C．3 D．4 【解析】 ∵BC∥AD， ∴EC CD ＝EF AF ，AF AE ＝CD DE ，故①④正确． ∵BF∥AD， ∴FG AG ＝BG GD ，故②正确． 【答案】 C 2．如图 1217，E 是▱ABCD 的边 AB 延长线上的一点，且DC BE ＝3 2 ，则AD BF ＝ ( ) 图 1217 A.3 2 B.2 3 C.5 2 D.2 5 【解析】 ∵CD∥AB，∴CD BE ＝FD EF ＝3 2 ， 又 AD∥BC，∴BF AD ＝EF ED. 由FD EF ＝3 2 ，得FD＋EF EF ＝3＋2 2 ， 即ED EF ＝5 2 ， ∴AD BF ＝ED EF ＝5 2.故选 C. 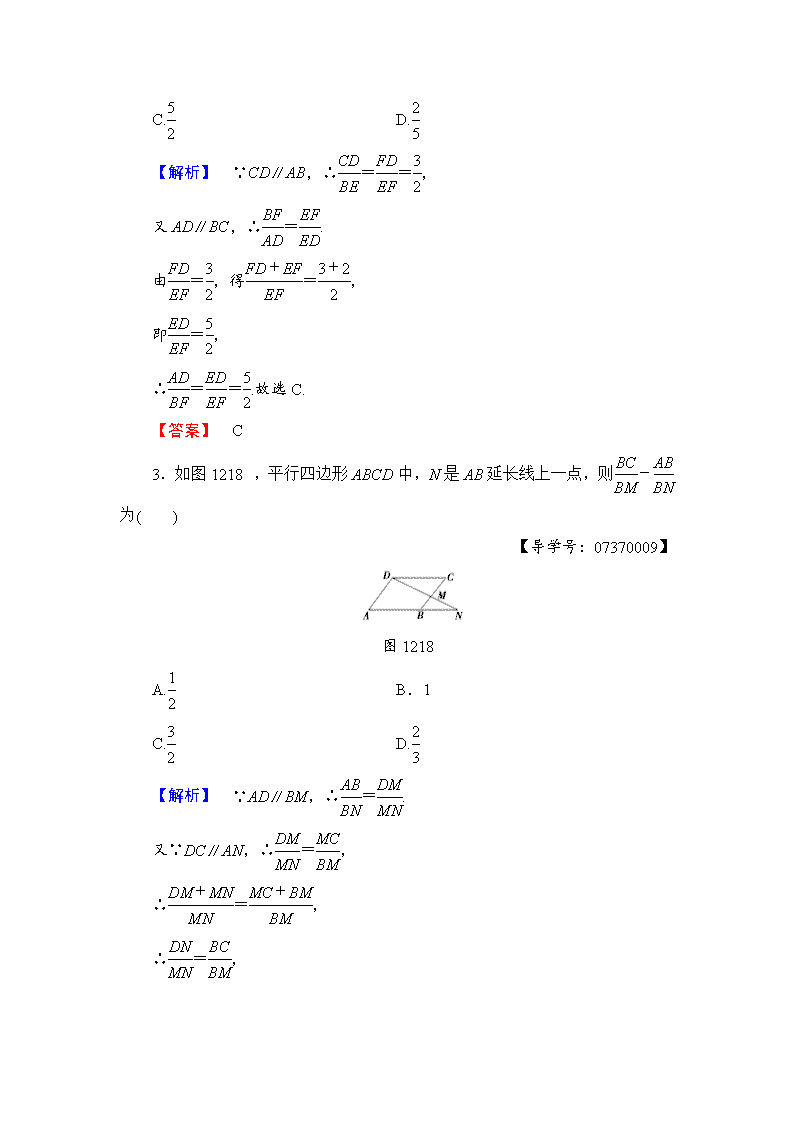【答案】 C 3．如图 1218，平行四边形 ABCD 中，N 是 AB 延长线上一点，则BC BM －AB BN 为( ) 【导学号：07370009】 图 1218 A.1 2 B．1 C.3 2 D.2 3 【解析】 ∵AD∥BM，∴AB BN ＝DM MN. 又∵DC∥AN，∴DM MN ＝MC BM ， ∴DM＋MN MN ＝MC＋BM BM ， ∴DN MN ＝BC BM ， ∴BC BM －AB BN ＝DN MN －DM MN ＝MN MN ＝1. 【答案】 B 4．如图 1219，AD 是△ABC 的中线，E 是 CA 边的三等分点，BE 交 AD 于 点 F，则 AF∶FD 为( ) 图 1219 A．2∶1 B．3∶1 C．4∶1 D．5∶1 【解析】 过 D 作 DG∥AC 交 BE 于 G， 如图，因为 D 是 BC 的中点， 所以 DG＝1 2EC， 又 AE＝2EC， 故 AF∶FD＝AE∶DG＝2EC∶1 2EC＝4∶1. 【答案】 C 5．如图 1220，将一块边长为 12 的正方形纸 ABCD 的顶点 A，折叠至边上 的点 E，使 DE＝5，折痕为 PQ，则线段 PM 和 MQ 的比是( ) 图 1220 A．5∶12 B．5∶13 C．5∶19 D．5∶21 【解析】 如图，作 MN∥AD 交 DC 于点 N， ∴DN NE ＝AM ME. 又∵AM＝ME， ∴DN＝NE＝1 2DE＝5 2 ， ∴NC＝NE＋EC＝5 2 ＋7＝19 2 . ∵PD∥MN∥QC， ∴PM MQ ＝DN NC ＝ 5 2 19 2 ＝ 5 19. 【答案】 C 二、填空题 6．(2016·乌鲁木齐)如图 1221，在△ABC 中，点 D，E 分别在 AB，AC 上， DE∥BC，AD＝CE，若 AB∶AC＝3∶2，BC＝10，则 DE 的长为__________． 图 1221 【解析】 ∵DE∥BC， ∴AD∶AE＝AB∶AC＝3∶2. ∵AD＝CE， ∴CE∶AE＝3∶2. ∵AE∶AC＝2∶5， ∴DE∶BC＝2∶5. ∵BC＝10， ∴DE∶10＝2∶5， 解得 DE＝4. 【答案】 4 7．如图 1222，已知 B 在 AC 上，D 在 BE 上，且 AB∶BC＝2∶1，ED∶ DB＝2∶1，则 AD∶DF＝________. 图 1222 【解析】 如图，过 D 作 DG∥AC 交 FC 于 G. 则DG BC ＝ED EB ＝2 3 ，∴DG＝2 3BC. 又 BC＝1 3AC，∴DG＝2 9AC. ∵DG∥AC，∴DF AF ＝DG AC ＝2 9 ， ∴DF＝2 9AF. 从而 AD＝7 9AF，∴AD∶DF＝7∶2. 【答案】 7∶2 8．如图 1223，在梯形 ABCD 中，AD∥BC，BD 与 AC 相交于 O，过 O 的 直线分别交 AB，CD 于 E，F，且 EF∥BC，若 AD＝12，BC＝20，则 EF＝________. 图 1223 【解析】 ∵AD∥EF∥BC，∴EO AD ＝BE AB ＝CF CD ＝FO AD ， ∴EO＝FO，而EO BC ＝AE AB ＝AB－BE AB ，EO AD ＝BE AB ，BC＝20，AD＝12， ∴EO 20 ＝1－BE AB ＝1－EO 12 ，∴EO＝7.5，∴EF＝15. 【答案】 15 三、解答题 9．线段 OA⊥OB，点 C 为 OB 中点，D 为线段 OA 上一点．连接 AC，BD 交于点 P.如图 1224，当 OA＝OB，且 D 为 OA 中点时，求AP PC 的值． 图 1224 【解】 过 D 作 DE∥CO 交 AC 于 E， 因为 D 为 OA 中点， 所以 AE＝CE＝1 2AC，DE CO ＝1 2 ， 因为点 C 为 OB 中点，所以 BC＝CO，DE BC ＝1 2 ， 所以PE PC ＝DE BC ＝1 2 ，所以 PC＝2 3CE＝1 3AC，所以AP PC ＝AC－PC PC ＝ 2 3AC 1 3AC ＝2. 10．如图 1225，AB⊥BD 于 B，CD⊥BD 于 D，连接 AD，BC 交于点 E， EF⊥BD 于 F，求证： 1 AB ＋ 1 CD ＝ 1 EF. 【导学号：07370010】 图 1225 【证明】 ∵AB⊥BD，CD⊥BD，EF⊥BD， ∴AB∥EF∥CD， ∴EF AB ＝DF BD ，EF CD ＝BF BD ， ∴EF AB ＋EF CD ＝DF BD ＋BF BD ＝DF＋BF BD ＝BD BD ＝1， ∴ 1 AB ＋ 1 CD ＝ 1 EF. [能力提升] 1．如图 1226，已知△ABC 中，AE∶EB＝1∶3，BD∶DC＝2∶1，AD 与 CE 相交于 F，则EF FC ＋AF FD 的值为( ) 图 1226 A.1 2 B．1 C.3 2 D．2 【解析】 过点 D 作 DG∥AB 交 EC 于点 G，则DG BE ＝ CD BC ＝CG EC ＝1 3.而AE BE ＝1 3 ，即AE BE ＝DG BE ，所以 AE＝DG，从而有 AF＝FD，EF＝FG ＝CG，故EF FC ＋AF FD ＝ EF 2EF ＋AF AF ＝1 2 ＋1＝3 2. 【答案】 C 2．如图 1227，已知 P，Q 分别在 BC 和 AC 上，BP CP ＝2 5 ，CQ QA ＝3 4 ，则AR RP ＝ ( ) 图 1227 A．3∶14 B．14∶3 C．17∶3 D．17∶14 【解析】 过点 P 作 PM∥AC， 交 BQ 于 M，则AR RP ＝AQ PM. ∵PM∥AC 且BP CP ＝2 5 ， ∴QC PM ＝BC BP ＝7 2. 又∵CQ QA ＝3 4 ，∴AQ PM ＝QC PM·AQ QC ＝7 2 ×4 3 ＝14 3 ， 即AR RP ＝14 3 . 【答案】 B 3.如图 1228 所示，在梯形 ABCD 中，AB∥CD，AB＝4，CD＝2.E，F 分别 为 AD，BC 上点，且 EF＝3，EF∥AB，则梯形 ABFE 与梯形 EFCD 的面积比为 __________． 图 1228 【解析】 如图，延长 AD，BC 交于点 O，作 OH⊥AB 于点 H. ∴ x x＋h1 ＝2 3 ，得 x＝2h1， x＋h1 x＋h1＋h2 ＝3 4 ，得 h1＝h2. ∴S 梯形 ABFE＝1 2 ×(3＋4)×h2＝7 2h1， S 梯形 EFCD＝1 2 ×(2＋3)×h1＝5 2h1， ∴S 梯形 ABFE∶S 梯形 EFCD＝7∶5. 【答案】 7∶5 4．某同学的身高为 1.6 m，由路灯下向前步行 4 m，发现自己的影子长为 2 m， 求这个路灯的高． 【解】 如图所示，AB 表示同学的身高，PB 表示该同学 的影长，CD 表示路灯的高，则 AB＝1.6 m，PB＝2 m，BD＝ 4 m. ∵AB∥CD， ∴PB PD ＝AB CD ， ∴CD＝AB×PD PB ＝1.6×2＋4 2 ＝4.8(m)， 即路灯的高为 4.8 m.