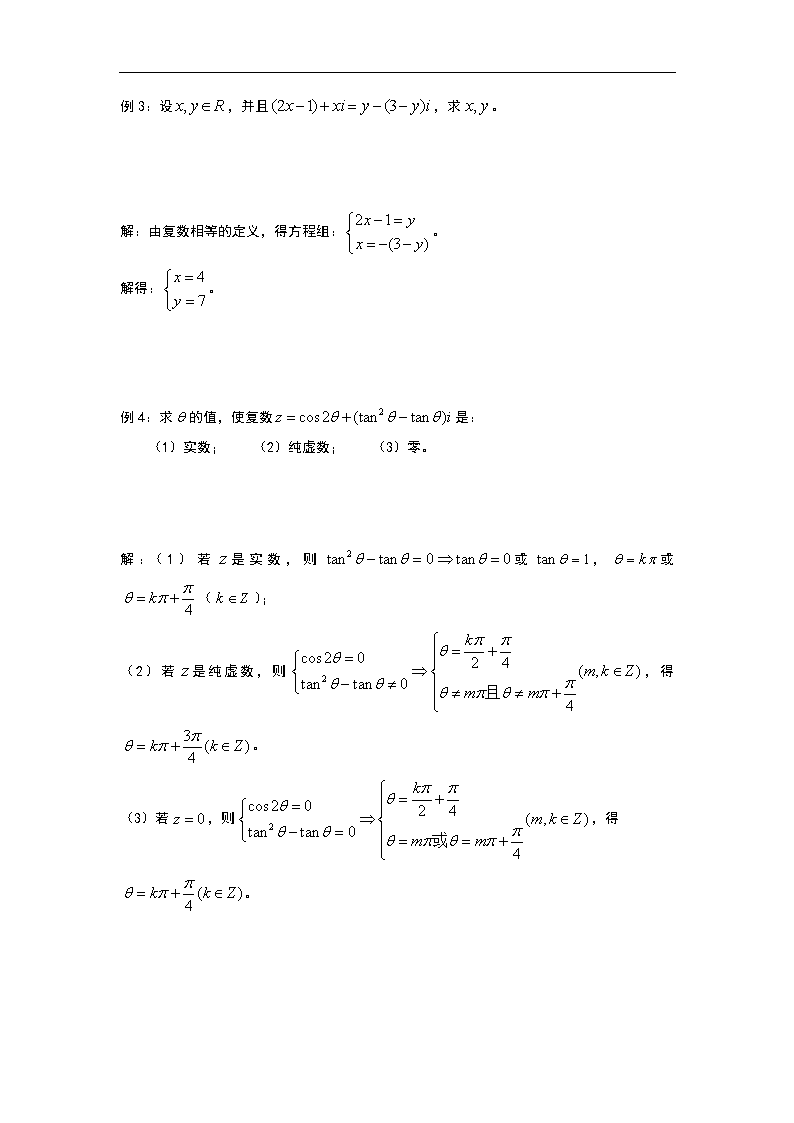高中同步数学教案第13章 复数 24页

第十三章 复数 一、复数的概念 ‎ 数的概念是在实践中一步步发展起来的。我们知道，实系数一元二次方程当其根的判别式“△＜”时，在实数范围内方程无解。再如：这样简单的方程在实数范围内无解。十六世纪，人们为了解决负数的开方问题，引入了一个新数，叫做虚数单位.‎ ‎1、——虚数单位 ‎ 规定：① ；‎ ‎ ②实数可以与进行四则运算，原有的加乘运算律仍适用。‎ ‎2、复数的定义 设都是实数，我们把形如的数叫做复数（是虚数单位）。‎ 全体复数的集合叫做复数集，常用字母C表示。‎ ‎3、复数的分类 对于复数，与分别叫做复数的实部与虚部，并且分别用符号和表示。‎ 对于复数，当时，就是实数；当时，叫做虚数。特别地，当并且时，叫做纯虚数。‎ 由此可以看出，实数集R是复数集C的真子集，有。‎ ‎4、复数的相等：‎ 对于两个复数，当且仅当它们的实部与虚部分别相等，这两个复数相等。即：‎ ‎ （其中 ‎5、两个复数不全为实数时，不能比较大小。‎ 例1：说出下列复数的实部与虚部，并指出它们是实数还是虚数，如果是虚数，还应指出是否为纯虚数。‎ ‎ （1）； （2）；‎ ‎ （3）； （4）。‎ 解：（1）的实部与虚部分别是与，它是虚数，但不是纯虚数；‎ ‎（2）的实部与虚部分别是和，它是虚数，而且是纯虚数；‎ ‎（3）的实部与虚部都是，它是实数；‎ ‎（4）的实部与虚部分别是与，它是虚数，当时它是纯虚数。‎ 说明：复数（虚部是不是。‎ 例2：已知复数，根据下列条件求实数的取值范围。‎ ‎（1）； （2）是虚数；‎ ‎（3）是纯虚数； （4）。‎ 解：（1），则，得或；‎ ‎（2）是虚数，则，得且；‎ ‎（3）若是纯虚数，则，得；‎ ‎（4）由，则，即，解得：或。‎ 例3：设，并且，求。‎ 解：由复数相等的定义，得方程组：。‎ 解得：。‎ 例4：求的值，使复数是：‎ ‎（1）实数；　　（2）纯虚数；　　（3）零。‎ 解：（1）若是实数，则或，或（）；‎ ‎（2）若是纯虚数，则，得。‎ ‎（3）若，则，得 ‎。‎ 二、复数的坐标表示 复数⇌直角坐标平面内的点⇌平面向量 .‎ ‎1、复平面的概念：‎ 建立直角坐标系来表示复数的平面叫做复平面.‎ ‎2、 实轴、虚轴：‎ 在复平面中，轴叫做实轴，轴叫做虚轴。实轴上的点都表示实数，虚轴上除原点以外的点都表示纯虚数。‎ 按这种表示方法，可知复数集C和复平面内的点构成了一一对应的关系。‎ O ‎3、复数的模：‎ 设复数在复平面上对应点为，那么点与原点O之间的距离叫做复数的模（也称为复数的绝对值），记作。由两点间距离公式，得：‎ ‎.‎ 例1：若复数对应点在第三象限内，求实数的取值范围。‎ 解：由题得：，所以实数的取值范围是。‎ 例2：已知，若分别为：‎ ‎（1）实数； （2）虚数； （3）纯虚数；‎ ‎（4）对应点在第二象限。求的值或取值范围。‎ 解：（因为。所以。‎ ‎（1）若为实数，则即，此时；‎ ‎（2）当时，为虚数；‎ ‎（3）若为纯虚数，则，此时；‎ ‎（4）若对应点在第二象限，则。‎ 例3：求证：在复平面内分别和复数，，，对应的四点共圆。‎ 证明：‎ 例4：设复数对应点.‎ 请在复平面上画出分别满足下列条件的点Z 所在的位置的区域(用阴影部分表示)‎ ‎ ‎ 三、复数的加法与减法 ‎1、复数加法与减法的运算法则：‎ 设与是任意的两个复数，它们的和与差分别是 ‎2、复数的加法满足交换律与结合律。即：设是三个任意的复数，则有：‎ 交换律：；‎ 结合律：。‎ ‎3、复数加法与复数减法的几何意义 若复数、对应的向量、不共线，则复数是以、为邻边的平行四边形对角线 所对应的复数；复数- 是联结向量、终点，并指向被减向量的向量所对应的复数。‎ ‎4、复平面上两点间的距离公式 设两复数、分别对应点，，则，两点之间的距离为 ‎5、共轭复数的概念：‎ 当两个复数的实部相等，虚部互为相反数时，这样的两个复数称为共轭复数。复数的共轭复数用表示。也就是说当时，。互为共轭的两复数在复平面上对应的点关于轴对称，且。‎ 例1：（1）已知复数，求证：的充分必要条件是；‎ ‎（2）设复数，求证：为纯虚数的充要条件是。‎ 证明：（1）设，则。若，则，所以；若，则，根据复数相等的意义，，所以。即的充分必要条件是。‎ ‎（2）设不同时为），。若为纯虚数，则，，；若，则，则，又，所以为纯虚数。即当时，为纯虚数的充要条件是。‎ 例2：已知复数Z满足，求的取值范围；‎ 解（1） ‎ ‎ 即对应点在以为圆心,‎ ‎ 半径为1的圆上(如图1)。‎ ‎ 表示圆上的 ‎ 点到点的距离.‎ 联结交圆于、两点（点在的延长线上） ‎ 结合图形，可知 又，‎ ‎，‎ ‎。‎ 例3：已知复数z满足|z-1-2i|-|z+2+i|=3 （i是虚数单位），若在复平面内z对应的点Z,则Z的轨迹为 （　　）‎ ‎ A.双曲线的一支 B.双曲线 ‎ C.一条射线 D.两条射线 例4：已知，求的取值范围。‎ 解：‎ 四、复数的乘法与除法 ‎1、复数乘法的运算法则：‎ 设是任意两个复数，复数的乘法按照以下法则进行：‎ 说明：复数的乘法与多项式的乘法是类似的，但在运算过程中要把换成，然后把实部与虚部分别合并。‎ ‎2、复数乘法的运算律 复数的乘法运算满足交换律、结合律以及乘法对加法的分配律。即对任意复数，有： ‎ ‎；‎ ‎3、复数的乘方 对于复数和自然数有 规定 ‎4、复数的除法法则：‎ 例1：计算: ① ②‎ 解：①。‎ ‎②。‎ 例2：已知一复数与其平方是互为共轭复数，求此复数。‎ 解：设，由题得：，即，根据复数相等的概念得：，由（2）得或，代入（1）‎ 当时，或；当时，。综上得，所求的复数有四个：‎ ‎。‎ 说明：这种方法是叫“复数问题实数化”，这种思想方法是解复数问题的常用方法。‎ 例3：（1）已知，求；‎ ‎（2）已知，复数，求的最大值与最小值。‎ 解：（1）由题知，，又，所以。即 ‎。‎ ‎（2）设，由，则 方法一：‎ ‎＝‎ 所以，由，得，所以，知的最大值为3，此时；最小值为0，此时，。‎ 方法二：由，那么，所以 ‎。以下同方法一。‎ 例4：设，解方程：。‎ 解：设，则，整理得 ‎，由复数相等的概念，所以方程的解为或。‎ 例5：已知是实数，且的实部与虚部相等，求。‎ 解：由题意得：，此时，所以。‎ 例6：已知复数。‎ ‎（1）设，求的值；‎ ‎（2）如果，求实数的值。‎ 解：（1）由，代入得：；‎ ‎（2），‎ 所以。‎ 例7：已知是虚数，是正实数，求证：是实数的充要条件是。‎ 证明：设，‎ 则，又 ‎，所以 ‎。‎ 例8：设复数满足。求的值和的取值范围。‎ 解：设，则，得 ‎。‎ 因为，所以，则。‎ 例9：已知且是纯虚数，求复数。‎ 解：方法一：设，则由题意得：，‎ 是纯虚数，所以，解得：‎ 或，所求复数为或。‎ 方法二：设，因为，所以 ‎，则，。‎ 方法三：设，则，即，所以 ‎，又，解得（以下同上）。‎ 例10：设是虚数，，且。‎ ‎①求的值及的取值范围；‎ ‎②设，求证：为纯虚数；‎ ‎③求的最小值。‎ 解：（1），。‎ ‎（2）为纯虚数 ‎（3）‎ 五、共轭复数与模的性质 ‎1、两个互为共轭复数的乘积 ‎2、，且是纯虚数 ‎3、复数的共轭运算性质：‎ 若，则有：‎ ‎（1）； （2）；‎ ‎（3）； （4）。‎ ‎（5）‎ 根据复数的加法、乘法的结合律，性质（1）、（3）还可以推广到个复数：‎ ‎；　　　‎ ‎。‎ ‎4、复数模的运算性质：‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎（4）‎ 例1：已知复数，求的模。‎ 解：20‎ 例2：设，求证：。‎ 证明：根据复数模的运算与共轭的关系得：‎ ‎＝。‎ 注：本例的几何意义是：平行四边形对角线的平方和等于四边的平方和。‎ 例3：已知，且，，求 解：‎ 例4：已知复数，，求：‎ 解：代入，‎ 例5：已知复数Z为虚数，且，若为实数，求 解：‎ 例6：已知复数Z满足，求的范围。‎ 解：‎ 例7：设，问：A、B能否比较大小？若能进行大小比较，请比较A、B的大小；若不能进行大小比较请说明理由。‎ 解：因为，所以，则A、B可以进行大小比较。‎ ‎，所以，当且仅当时，等号成立。‎ 六、复数的平方根与立方根 ‎1、幂运算的周期性：‎ 因为 ，若，根据复数乘法运算法则，有：‎ ‎。‎ ‎2、复数的平方根 ‎ ‎3、1的立方根、 运算的周期性 ‎ （，）满足 ‎； ；‎ ‎； ；‎ ‎； ‎ 例1：当时，计算所有可能的取值。‎ 解：2、0、-2‎ 例2：计算：‎ ‎（1）；　　　　　（2）；　　　　（3）（‎ 例3：求复数的平方根。‎ 解：设的平方根为，则由定义知：‎ ‎。即，解得 或。所以的平方根为或。‎ 例4：求值：（1）； （2）‎ 解：（1）； （2）‎ 例5：已知 则（1） ； （2） ；‎ ‎（3） ； （4） 。‎ 解：（1）-1； （2）2； （3）-1； （4）‎ 七、实系数一元二次方程：‎ ‎1、方程是实系数一元二次方程，其中是根的判别式。‎ ‎2、实系数一元二次方程的解：‎ 一般地，解实系数一元二次方程时，可以把原方程化为，由此可得：‎ ‎（1）当时，方程有两个不相等的实数根；‎ ‎（2）当时，方程有两个相等的实数根；‎ ‎（3）当时，方程有一对共轭虚根。‎ ‎3、实系数一元二次方程若有一对共轭虚根，韦达定理仍成立。‎ 当时，对于共轭虚根有：‎ ‎。‎ 例1：在:复数集内解下列方程：‎ ‎（1）；　　　　　　　（2）；‎ ‎（3）；　　 　（4）‎ 解：（4）若，则方程的解为；‎ 当时，。‎ ‎（1）若，即且时，方程有两个不等实数根，；‎ ‎（2）当即时，方程有两相等的实根；‎ ‎（3）当即时，方程有一对共轭虚根 综上知：时，方程解为；当时，方程解为，‎ ‎；当时，方程解为；当时，方程有一对共轭虚根。‎ 例2：（1）已知是关于的方程的一个根，求的值；‎ ‎（2）已知是关于的方程的一个根，求的值，并解此方程。‎ 解：（1）由，知方程是实系数一元二次方程，则它的根互为共轭，所以此方程两根为与。根据韦达定理得：‎ ‎；。‎ 即。‎ ‎（2）由是方程的根，则，即。‎ 设方程的另外一根为，则。‎ 例3：设是实系数方程的两个虚根，且，求的值。‎ 解：因为方程的两根是虚根，所以是一对共轭复数且，则 ‎，，所以。‎ 另一方法：因为是一对共轭虚数，所以是纯虚数，则，‎ 即，由韦达定理：。‎ 解后反思：若原题变为：‎ 设是实系数方程的两个根，且，求的值。如何求解？‎ 解：由题知，即，得或。‎ 注意：灵活运用韦达定理与复数模的相关性质求解比分类讨论简便。‎ 例4：设是方程的两根，求。‎ 解：‎ ‎（1）当，即时，方程两根，则有 ‎＝；‎ ‎（2）当，即时，方程两根是共轭虚根，所以 ‎＝。‎ 由此得：。‎ 另一方面：当，即时，方程两根是一对共轭虚根，即，根据韦达定理得：，所以，则。‎ 例5：设关于方程至少有一个根的模等于1，求实数的值。‎ 解：‎ 当，即或时，方程两根是实根。若，则，无实数解；若，则，解得。‎ 当，即时，方程两根为一对共轭虚根，则，解得：或（舍去）。综上知，或。‎ 例6：设、是实系数一元二次方程的两根，已知为虚数，为实数，求的值。‎ 解：‎ 例7：设方程有实数根，求出这个实数根。‎ 解：设这个方程的实数根为，则，整理得 ‎，由复数相等的意义得：‎ ‎，所以所求的根为。‎ 例8：已知关于的一元二次方程有实根，求满足的条件。‎ 解：设方程的实根为，则满足：‎ ‎，即，因为，由复数相等的条件得：。‎ 若，则，代入得：，即；‎ 若，则，同样满足。所以满足。‎ 八、复数集内解方程 例1：已知复数满足，求复数。‎ 解：由题知，所以。‎ 说明：本题在计算中学生会出现设的情况。这样计算较繁。‎ 例2：设，解方程。‎ 解：设，则，整理得 ‎，根据复数相等的意义有 解得：或。即所求的复数为或。‎ 例3：在复数集内解方程：。‎ 解：方法一：设，则，得：‎ ‎。‎ 若则，即或（舍），所以，此时；‎ 若，则或，所以或，此时方程的解为、。综上知方程的解有6个：。‎ 方法二：由，则，所以必是实数或是纯虚数。‎ 若，则由得或，所以或；‎ 若为纯虚数，设，则，方程为。‎ 即或（舍），得，则。‎ 综上知方程的解有6个：。‎ 例4：设，解方程。‎ 解：由且，可得，所以是纯虚数，又，则，只要求出即可。对两边取模得：‎ 即，。‎ 例5：证明：在复数范围内，方程没有解。‎ 证明：原方程化为：，设代入得：‎ ‎，则有，因为此方程根的判别式，此方程无实解。所以原方程在C上无解。‎