高一数学向量知识点 5页

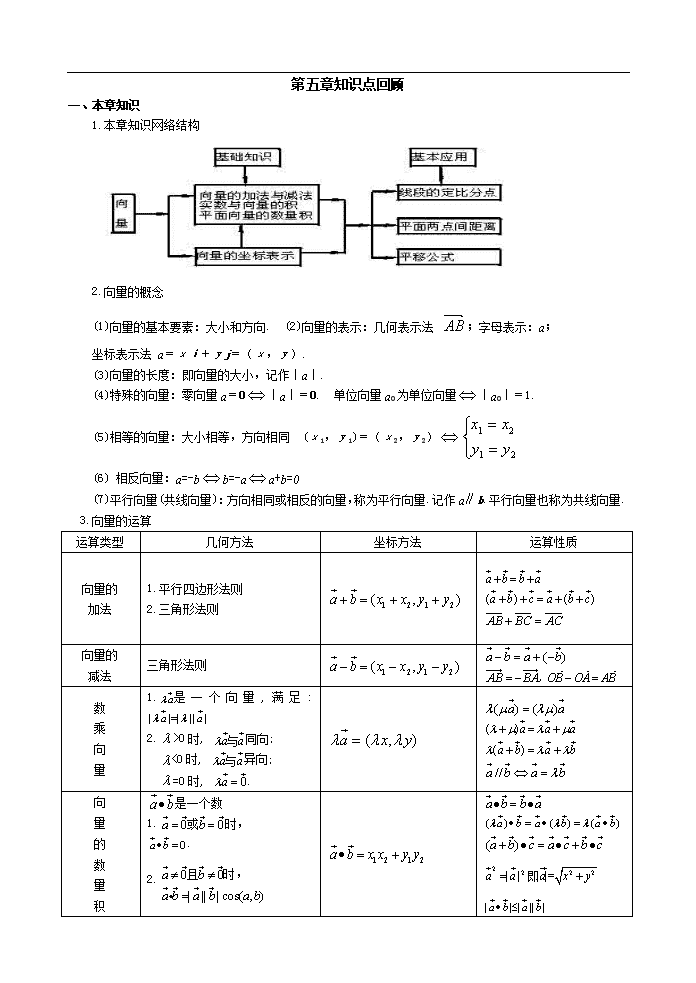
第五章知识点回顾 一、本章知识 ‎1.本章知识网络结构  ‎2.向量的概念 ‎(1)向量的基本要素：大小和方向.(2)向量的表示：几何表示法 ；字母表示：a；‎ 坐标表示法 a＝ｘｉ＋ｙj＝（ｘ，ｙ）. ‎(3)向量的长度：即向量的大小，记作｜a｜. ‎(4)特殊的向量：零向量a＝O｜a｜＝O.单位向量aO为单位向量｜aO｜＝1. ‎(5)相等的向量：大小相等，方向相同(ｘ1，ｙ1)＝（ｘ2，ｙ2）‎ ‎(6) 相反向量：a=-bb=-aa+b=0‎ ‎(7)平行向量(共线向量)：方向相同或相反的向量，称为平行向量.记作a∥b.平行向量也称为共线向量.3.向量的运算 运算类型 几何方法 坐标方法 运算性质 向量的 加法 ‎1.平行四边形法则 ‎2.三角形法则 向量的 减法 三角形法则 ‎,‎ 数 乘 向 量 ‎1.是一个向量,满足:‎ ‎2.>0时, 同向;‎ ‎<0时, 异向;‎ ‎=0时, .‎ 向 量 的 数 量 积 是一个数 ‎1.时，‎ ‎.‎ ‎2. ‎ ‎4.重要定理、公式 ‎(1)平面向量基本定理 e1，e2是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数λ1，‎ λ2，使a＝λ1e1＋λ2e2. ‎(2)两个向量平行的充要条件 a∥ba＝λb(b≠0)x1y2－x2y1＝O. ‎(3)两个向量垂直的充要条件 a⊥ba·b＝Ox1x2＋y1y2＝O. ‎(4)线段的定比分点公式 设点P分有向线段所成的比为λ，即＝λ，则 ‎＝＋ (线段的定比分点的向量公式) ‎ (线段定比分点的坐标公式) 当λ＝1时，得中点公式： ‎＝（＋）或 ‎ (5)平移公式 设点P(x，y)按向量a＝（ｈ，ｋ）平移后得到点P′（x′，y′），‎ 则＝+a或 曲线y＝f（x）按向量a＝（ｈ，ｋ）平移后所得的曲线的函数解析式为：y－ｋ＝f（x－ｈ)‎ ‎(6)正、余弦定理 正弦定理：‎ 余弦定理：a2＝b2＋c2－2bccosA， b2＝c2＋a2－2cacosB， c2＝a2＋b2－2abcosC. 反三角函数：反正弦函数、反余弦函数、反正切函数、反余切函数、反正割函数，反余割函数总称为反三角函数．‎ 函数y＝sinx，的反函数叫做反正弦函数，记作y＝arcsinx ‎，它的定义域是［－1，1］，值域是．‎ 函数y＝cosx，（x∈［0，π］）的反应函数叫做反余弦函数，记作y＝arccosx，它的定义域是［－1，1］，值域是［0，π］．‎ 函数y＝tgx，的反函数叫做反正切函数，记作y＝arctgx，它的定义域是（－∞，＋∞），值域是．‎ 函数y＝ctgx，［x∈（0，π）］的反函数叫做反余切函数，记作y＝arcctgx，它的定义域是（－∞，＋∞），值域是（0，π）．‎ ‎2、反三角函数的图象：‎ 利用函数y＝f（x）与y＝f′(x) 的图象关于直线y＝x对称的关系，可以画出各反三角函数的图象．‎ ‎3、反三角函数的定义域、值域及性质：‎ 函 数 y＝arcsinx y＝arccosx y＝arctgx y＝arcctgx 定义域 ‎［－1，1］‎ ‎［－1，1］‎ ‎（－∞，＋∞）‎ ‎（－∞，＋∞）‎ 值 域 ‎［0，π］‎ ‎（0，π）‎ 奇偶性 奇函数 非奇非偶函数 奇函数 非奇非偶函数 有界性 有界函数 有界函数 有界函数 有界函数 单调性 递增 递减 递增 递减 ‎4、反三角函数的三角运算：‎ 求用反三角函数所表示的角的三角函数以及三角函数对反三角函数间的和、差、倍角的运算．‎ ‎（1）三角函数对同名的反三角函数的运算：‎ ‎（－1≤x≤1）‎ sin（arcsinx）＝x cos（arccosx）＝x ‎（－∞＜x＜＋∞）‎ tg（arctgx）＝x ctg（arcctgx）＝x ‎（2）三角函数对异名的反三角函数的运算 arcsinx arccosx arctgx arcctgx sin x ‎（－1≤x≤1）‎ ‎（－1≤x≤1）‎ cos ‎（－1≤x≤1）‎ x ‎（－1≤x≤1）‎ tg ‎（－1＜x＜1）‎ ‎（－1≤x≤1，且x≠0）‎ x ‎（x≠0）‎ ctg ‎（－1≤x≤1，x≠0）‎ ‎（－1＜x＜1）‎ ‎（x≠0）‎ x y＝arccscx ‎5、反三角函数间的基本关系式：‎ ‎1．x与－x的反三角函数间的关系 arcsin（－x）＝－arcsinx， x∈［－1，1］ ①‎ arctg（－x）＝－arctgx， x∈（－∞，＋∞） ②‎ arccos（－x）＝π－arccosx， x∈［－1，1］ ③‎ arcctg（－x）＝π－arcctgx， x∈（－∞，＋∞） ④‎ ‎③、④也叫互补关系．‎ ‎2．互余关系 arcsinx＋arccosx＝，x∈［－1，1］ ①‎ arctgx＋arcctgx＝， ②‎