2021届高考数学一轮总复习第二章函数导数及其应用课时作业11函数与方程含解析苏教版 5页

课时作业11　函数与方程 一、选择题 ‎1．函数f(x)＝(lnx)2－3lnx＋2的零点是(　D　)‎ A．(e,0)或(e2,0) B．(1,0)或(e2,0)‎ C．1或e2 D．e或e2‎ 解析：f(x)＝(lnx)2－3lnx＋2＝(lnx－1)(lnx－2)，由f(x)＝0得x＝e或x＝e2，故选D.‎ ‎2．函数f(x)＝＋a的零点为1，则实数a的值为(　B　)‎ A．－2 B．－ C. D．2‎ 解析：函数f(x)＝＋a的零点为1，所以f(1)＝＋a＝0，解得a＝－.‎ ‎3．函数f(x)＝2x＋log2x－3在区间(1,2)内的零点个数是(　B　)‎ A．0 B．1‎ C．2 D．3‎ 解析：由题意得函数f(x)在(0，＋∞)上单调递增，且f(1)＝－1，f(2)＝2，则f(1)f(2)<0，根据零点存在性定理可得，函数f(x)在区间(1,2)内有1个零点，故选B.‎ ‎4．若函数f(x)＝ax＋b有一个零点是2，则函数g(x)＝bx2－ax的零点是(　C　)‎ A．0,2 B．0， C．0，－ D．2，－ 解析：∵函数f(x)＝ax＋b有一个零点是2，∴‎2a＋b＝0，∴g(x)＝－2ax2－ax＝－ax(2x＋1)，∴函数g(x)的零点为0和－，故选C.‎ ‎5．方程4x2＋(m－2)x＋m－5＝0的一根在区间(－1,0)内，另一根在区间(0,2)内，则m的取值范围是(　B　)‎ A. B． C.∪(5，＋∞) D． 解析：设f(x)＝4x2＋(m－2)x＋m－5，‎ ‎∵方程4x2＋(m－2)x＋m－5＝0的一根在区间(－1,0)内，另一根在区间(0,2)内，‎ ‎∴即 5‎ 解得－b，c>d.若f(x)＝2 019＋(x－a)(x－b)的零点为c，d，则下列不等式正确的是(　A　)‎ A．a>c>d>b B．a>b>c>d C．c>d>a>b D．c>a>b>d 解析：设g(x)＝(x－a)(x－b)，则g(x)的零点为a，b.函数f(x)＝2 019＋g(x)的图象可看作函数y＝g(x)的图象向上平移2 019个单位，如图所示，则有a>c>d>b，所以选A.‎ ‎7．(2020·湖南娄底模拟)若x1是方程xex＝1的解，x2是方程xlnx＝1的解，则x1x2等于(　A　)‎ A．1 B．－1‎ C．e D． 解析：考虑到x1，x2是函数y＝ex、函数y＝lnx分别与函数y＝的图象的公共点A，B的横坐标，而A，B两点关于直线y＝x对称，因此x1x2＝1.故选A.‎ ‎8．(2019·浙江卷)设a，b∈R，函数f(x)＝‎ 若函数y＝f(x)－ax－b恰有3个零点，则(　C　)‎ A．a<－1，b<0 B．a<－1，b>0‎ C．a>－1，b<0 D．a>－1，b>0‎ 解析：由题意可得，当x≥0时，f(x)－ax－b＝x3－(a＋1)x2－b，令f(x)－ax－b＝0，则b＝x3－(a＋1)x2＝x2[2x－3(a＋1)]．因为对任意的x∈R，f(x)－ax－b＝0有3个不同的实数根，所以要使满足条件，则当x≥0时，b＝x2[2x－3(a＋1)]必须有2个零点，所以>0，解得a>－1.所以b<0.故选C.‎ 二、填空题 ‎9．函数f(x)＝x－x的零点个数为1.‎ 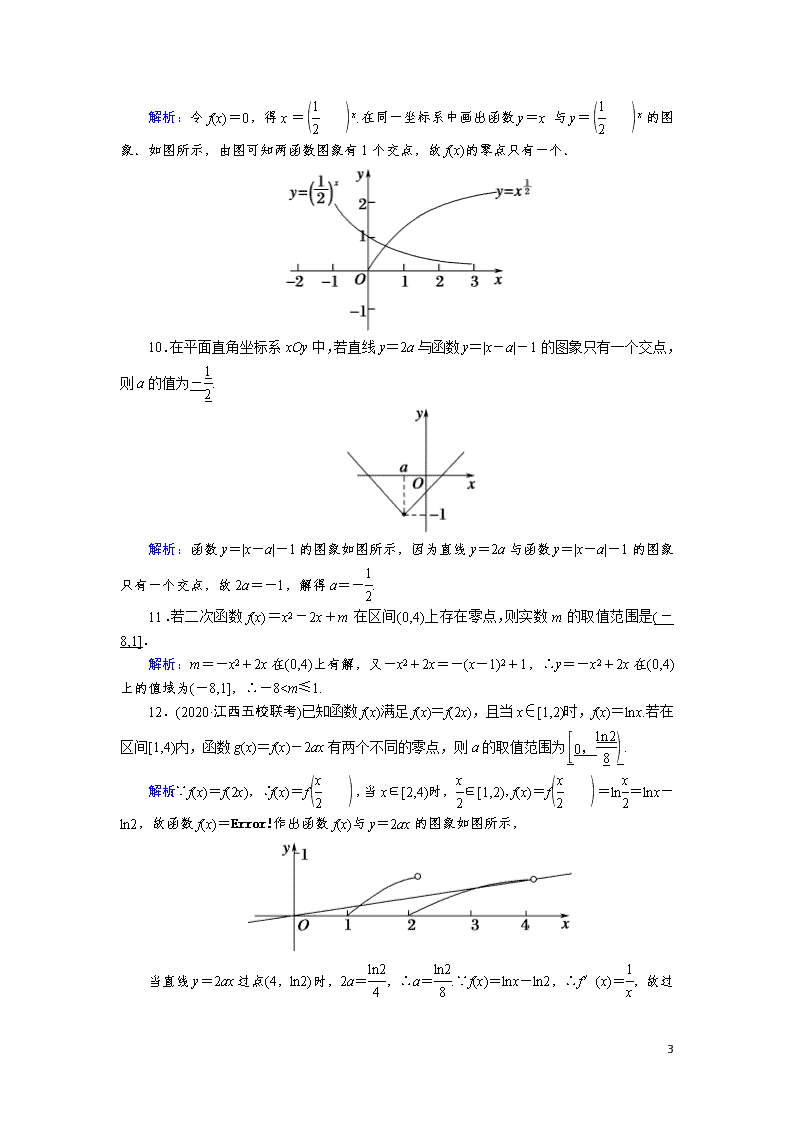解析：令f(x)＝0，得x＝x.在同一坐标系中画出函数y＝x与y＝x的图象．如图所示，由图可知两函数图象有1个交点，故f(x)的零点只有一个．‎ 5‎ ‎10．在平面直角坐标系xOy中，若直线y＝‎2a与函数y＝|x－a|－1的图象只有一个交点，则a的值为－.‎ 解析：函数y＝|x－a|－1的图象如图所示，因为直线y＝‎2a与函数y＝|x－a|－1的图象只有一个交点，故‎2a＝－1，解得a＝－.‎ ‎11．若二次函数f(x)＝x2－2x＋m在区间(0,4)上存在零点，则实数m的取值范围是(－8,1]．‎ 解析：m＝－x2＋2x在(0,4)上有解，又－x2＋2x＝－(x－1)2＋1，∴y＝－x2＋2x在(0,4)上的值域为(－8,1]，∴－84.过原点与f(x)＝lnx的图象相切的直线的斜率＝，得x＝e>2.故实数a的取值范围是.‎ 三、解答题 ‎13．已知y＝f(x)是定义域为R的奇函数，当x∈[0，＋∞)时，f(x)＝x2－2x.‎ 5‎ ‎(1)写出函数y＝f(x)的解析式；‎ ‎(2)若方程f(x)＝a恰有3个不同的解，求实数a的取值范围．‎ 解：(1)设x<0，则－x>0，‎ 所以f(－x)＝x2＋2x.又因为f(x)是奇函数，‎ 所以f(x)＝－f(－x)＝－x2－2x.‎ 所以f(x)＝ ‎(2)方程f(x)＝a恰有3个不同的解，即y＝f(x)与y＝a的图象有3个不同的交点．作出y＝f(x)与y＝a的图象如图所示，故若方程f(x)＝a恰有3个不同的解，只需－10.所以f(x)min＝f(1)＝－‎4a＝－4，a＝1.‎ 故函数f(x)的解析式为f(x)＝x2－2x－3.‎ ‎(2)因为g(x)＝－4lnx＝x－－4lnx－2(x>0)，所以g′(x)＝1＋－＝.‎ 令g′(x)＝0，得x1＝1，x2＝3.‎ 当x变化时，g′(x)，g(x)的取值变化情况如下：‎ x ‎(0,1)‎ ‎1‎ ‎(1,3)‎ ‎3‎ ‎(3，＋∞)‎ g′(x)‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ g(x)‎  极大值  极小值  当00时，f(x)是增函数，f(3)＝0，则函数g(x)＝f(x)＋lg|x＋1|的零点个数为3.‎ 解析：画出函数y＝f(x)和y＝－lg|x＋1|的大致图象，如图所示．∴由图象知，函数g(x)＝f(x)＋lg|x＋1|的零点的个数为3.‎ 5‎