广东省七校联合体2020届高三第一次联考数学（理）试题 Word版含答案 12页

七校联合体2020届高三第一次联考试卷（8月）‎ 理科数学 命题学校：中山市第一中学 命题人： 审题人： ‎ 本试卷6页，23小题，满分150分。考试用时120分钟。‎ 注意事项：1．答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。‎ ‎2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑；如需要改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试卷上。‎ ‎3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。‎ ‎4．考生必须保证答题卡的整洁。考试结束后，将试卷和答题卡一并交回。‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项符合题目要求。‎ ‎1.已知集合，集合，则（ ）‎ A． B． C． D．‎ ‎2.已知为虚数单位，，则在复平面上复数的共轭复数对应的点位于（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎ ‎3.为比较甲、乙两名高中学生的数学素养，对课程标准中规定的数学六 大素养进行指标测验（指标值满分为5分，分值高者为优），根据测验情 况绘制了如图所示的六大素养指标雷达图，则下面叙述正确的是（ ）‎ A．乙的数据分析素养优于甲 B．乙的数学建模素养优于数学抽象素养 12‎ C．甲的六大素养整体水平优于乙 D．甲的六大素养中数据分析最差 ‎ ‎4. 已知则（ ）‎ A． B． C． D． ‎ ‎5.已知抛物线与双曲线的焦点相同，双曲线的离心率为（ ）‎ A. B. C. D. 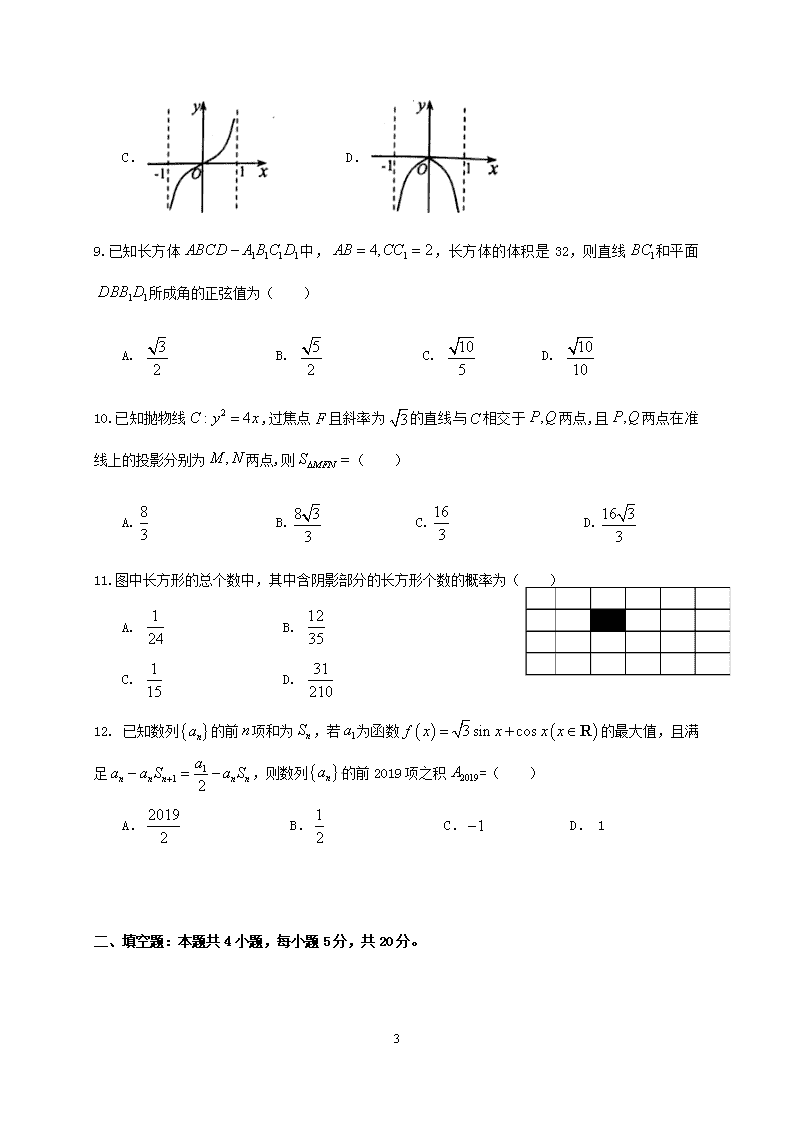‎ ‎6.若函数的最小正周期为，若将其图象向左平移个单位，得到函数的图象，则函数的解析式为（ ）‎ A． B．‎ C． D． ‎ ‎7.在直角梯形中，，，是的中点，则（ ）‎ A． B． ‎ C． D． ‎ ‎8.设函数，则函数的图象可能为（ ）‎ A． B．‎ 12‎ C． D．‎ ‎9.已知长方体中，，长方体的体积是32，则直线和平面所成角的正弦值为（ ）‎ A. B. C. D. ‎10.已知抛物线,过焦点且斜率为的直线与相交于两点,且两点在准线上的投影分别为两点,则（ ）‎ A. B. C. D.‎ ‎11.图中长方形的总个数中，其中含阴影部分的长方形个数的概率为（ ） ‎ A. B. ‎ C. D. ‎12. 已知数列的前项和为，若为函数的最大值，且满足，则数列的前2019项之积=（ ）‎ A． B． C． D． 1‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ 12‎ 13. 若满足约束条件，则的最大值是_______．‎ ‎14． 的展开式中，常数项是______．‎ ‎15．已知四棱锥中，底面是矩形，，是等边三角形，且平面平面，若四棱锥的外接球的表面积为，则__________． ‎ ‎16. 已知，是函数在，内的两个零点，则__________．‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎ 17.（本小题满分12分）已知数列满足．‎ ‎（1）求、；‎ ‎（2）求证：数列为等差数列；‎ ‎（3）求数列的前项和．‎ ‎ 18.（本小题满分12分）四棱锥中，为矩形，平面平面.‎ A B C D P ‎（1）求证：‎ ‎（2）若问为何值时，四棱锥的体积最大？并求此时平面与平面夹角的余弦值.‎ 12‎ ‎19．（本小题满分12分）计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量X（年入流量：一年内上游来水与库区降水之和，单位：亿立方米）都在40以上．其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年．将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立．‎ ‎（1）求未来4年中，至多有1年的年入流量超过120的概率；‎ ‎（2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量X限制，并有如下关系：‎ 年入流量 发电机最多可运行台数 ‎　若某台发电机运行，则该台年利润为5 000万元；若某台发电机未运行，则该台年亏损800万元．欲使水电站年总利润的均值达到最大，应安装发电机多少台？‎ ‎20.（本小题满分12分）已知函数，其中，e为自然对数的底数.‎ ‎（I）当时，证明：对，.‎ ‎（II）若函数在上存在极值，求实数的取值范围.‎ ‎21.（本小题满分12分）已知圆和定点，是圆上任意一点，线段的垂直平分线交于点，设点的轨迹为．‎ ‎（Ⅰ）求的方程；‎ ‎（Ⅱ）若直线与曲线相交于，两点，试问：在轴上是否存在定点，使当变化时，总有？若存在，求出点的坐标；若不存在，请说明理由．‎ 12‎ ‎（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22．[选修4―4：坐标系与参数方程]（10分）‎ 在直角坐标系中，直线的参数方程为（为参数，），以原点为极点，轴的正半轴为极轴，建立极坐标系.曲线的极坐标方程为：‎ ‎.‎ ‎（1）求曲线的直角坐标方程和直线的普通方程；‎ ‎（2）设直线与曲线相交于，两点，当到直线的距离最大时，求.‎ ‎23.[选修4—5：不等式选讲]（10分）‎ 已知函数 求不等式的解集；‎ 若函数的最大值为，正实数满足，求证：．‎ 12‎ 七校联合体2020届高三第一次联考试卷（8月）理科数学参考答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A A C B C D D C C B B C 二、填空题：‎ ‎13.2 14. 6 15. 4 16. ‎ 三、解答题： ‎ ‎17.解（1），，‎ ‎，； ………… 3分 ‎（2），‎ ‎ ， ，‎ 数列是首项为1，公差为1的等差数列； ………… 7分 ‎（3）由（2）知：，‎ ‎ …… 12分 ‎18.解析：（1）证明：为矩形，故， ………… 1分 又平面平面，平面平面，所以平面 3分 因为平面，故 ………… 4分 ‎（2）解：过作的垂线，垂足为，过作的垂线，垂足为，连接.‎ 故平面，平面,‎ 12‎ 在直角三角形中，‎ 设，则，故四棱锥的体积为 ‎ ………… 6分 因为 故当时，即时，四棱锥的体积最大. ………… 8分 建立如图所示的空间直角坐标系，‎ 故 设平面的法向量，则由得 ‎，不妨取，则. ……… 10分 同理可求出平面的法向量， ………… 11分 设平面与平面夹角为，则 ‎ 又因为为锐角，所以 ………… 12分 12‎ ‎19.解：（1）依题意，，，‎ ‎. 由二项分布，在未来4年中至多有1年的年入流量超过120的概率为. …… 5分 ‎（2）记水电站年总利润为（单位：万元）．‎ ‎①安装1台发电机的情形．‎ 由于水库年入流量总大于40，故1台发电机运行的概率为1，对应的年利润，‎ ‎ .…… 7分 ‎②安装2台发电机的情形．‎ 依题意，当时，1台发电机运行，此时，因此；‎ ‎4 200‎ ‎10 000‎ ‎0.2‎ ‎0.8‎ 当时，2台发电机运行，此时，因此；由此得的分布列如下：‎ 所以，. .…… 9分 ‎ ‎③安装3台发电机的情形．‎ 依题意，当时，1台发电机运行，此时，因此；当时，2台发电机运行，此时，因此；当时，3台发电机运行，此时，因此，由此得的分布列如下 ‎3 400‎ ‎9 200‎ ‎15 000‎ ‎0.2‎ ‎0.7‎ ‎0.1‎ 所以， .…… 11分 ‎ 12‎ 综上，欲使水电站年总利润的均值达到最大，应安装发电机2台．-------------12分 ‎20.解（1）当时，，于是. …………………… 1分 又因为，当时，且.‎ 故当时，，即. ……………………………………3分 所以，函数为上的增函数，于是.‎ 因此，对，；……………………………………………………… 5分 ‎（2） 由题意在上存在零点…………………6分 ①当时，为上的增函数，‎ 注意到，，所以，存在唯一实数，使得成立. ‎ 于是，当时，，为上的减函数；‎ 当时，，为上的增函数；‎ 所以为函数的极小值点；--------------------------------------------8分 ②当时，在上成立，‎ 所以在上单调递增，所以在上没有极值； ----------10分 ‎ ③当时，在上成立，‎ 所以在上单调递减，所以在上没有极值， ‎ 综上所述，使在上存在极值的的取值范围是.------------ 12分 12‎ ‎21.解：（Ⅰ）圆，圆心，由已知得，又，‎ 所以，所以由椭圆的定义知点的轨迹是以，为焦点的椭圆， ------2分 设其标准方程，则，，所以，，所以曲线．-----4分 ‎（Ⅱ）设存在点满足题设，联立直线与椭圆方程消得 ‎， -----6分 设，，，，则由韦达定理得①，②， -----8分 ‎ 由题设知平分直线与直的倾斜角互补，即直线与直线的斜率之和为零，‎ 即，即，‎ 即③， 把①、②代入③并化简得，即④， -----10分 所以当变化时④成立，只要即可， 所以存在定点满足题设． ------12分 ‎22.解：（1）曲线：，即：.‎ 代入得曲线的直角坐标方程为：. ------2分 当直线的参数方程可化为（为参数）， ‎ 所以直线的普通方程为 ------3分 当时，直线的参数方程（为参数，）消去参数直线的普通方程为 ------5分 ‎（2）设，当到直线的距离最大时，，故. ------6分 ‎∴的参数方程为（为参数）， ------7分 12‎ 将直线的参数方程代入得：.‎ ‎∴， ------8分 ‎∴. ------10分 ‎23.解： ------1分 当时，； ------2分 当时，得，所以 ------3分 当时，恒成立， ------4分 原不等式的解集为 ------5分 ‎ 所以 ------7分 ‎ ‎ ------9分 ‎ ------10分 12‎