高中数学人教A版必修四全册教案3_2简单的三角恒等变换（三） 2页

‎3.2简单的三角恒等变换（三）‎ 教学目标 （一） 知识与技能目标 熟练掌握三角公式及其变形公式．‎ （二） 过程与能力目标 抓住角、函数式得特点，灵活运用三角公式解决一些实际问题．‎ （三） 情感与态度目标 培养学生观察、分析、解决问题的能力．‎ 教学重点 和、差、倍角公式的灵活应用．‎ 教学难点 如何灵活应用和、差、倍角公式的进行三角式化简、求值、证明．‎ 教学过程 例1：教材P141面例4‎ 例1. 如图，已知OPQ是半径为1，圆心角为的扇形，C是扇形弧上的动点，ABCD是扇形的内接矩形.记∠COP＝a，求当角a取何值时，矩形ABCD的面积最大？并求出这个最大面积.‎ θ 例2：把一段半径为R的圆木锯成横截面为矩形的木料，怎样锯法能使横截面的面积最大？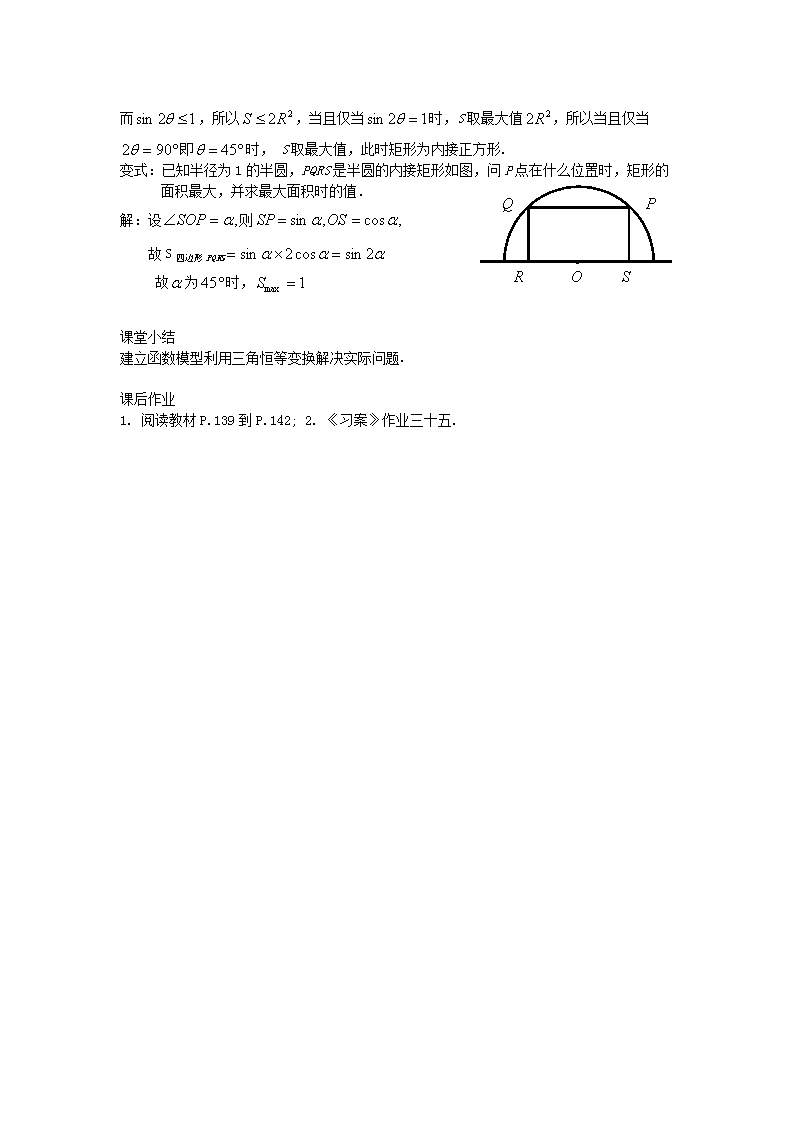（分别设边与角为自变量）‎ 解：（1）如图，设矩形长为l，则面积，‎ 所以当且仅当 即时，取得最大值，此时S取得最大值，矩形的宽为 即长、宽相等，矩形为圆内接正方形.‎ ‎（2）设角为自变量，设对角线与一条边的夹角为，矩形长与宽分别为 ‎、，所以面积.‎ 而，所以，当且仅当时，S取最大值，所以当且仅当即时， S取最大值，此时矩形为内接正方形.‎ P Q R S O 变式：已知半径为1的半圆，PQRS是半圆的内接矩形如图，问P点在什么位置时，矩形的面积最大，并求最大面积时的值．‎ 解：设则 故S四边形PQRS 故为时，‎ 课堂小结 ‎ 建立函数模型利用三角恒等变换解决实际问题.‎ 课后作业 ‎ ‎1. 阅读教材P.139到P.142; 2. 《习案》作业三十五.‎