高中数学必修2第一章空间几何体试题(含答案) 6页

高一数学必修 2 第一章测试题 班别 姓名 考号 得分 一、选择题：（每小题 5 分，共 50 分） 1. 下图中的几何体是由哪个平面图形旋转得到的（ ） A B C D 2．若一个几何体的三视图都是等腰三角形，则这个几何体可能是（ ） A．圆锥 B．正四棱锥 C．正三棱锥 D．正三棱台 3.已知圆柱与圆锥的底面积相等，高也相等，它们的体积分别为 V1 和 V2，则 V1：V2=（ ） A. 1：3 B. 1：1 C. 2：1 D. 3：1 4.过圆锥的高的三等分点作平行于底面的截面，它们把圆锥侧面分成的三部分的面积之比为 （ ） A.1：2：3 B.1：3：5 C.1：2：4 D.1：3：9 5.棱长都是 1 的三棱锥的表面积为（ ） A. 3 B. 32 C. 33 D. 34 6.如果两个球的体积之比为 8:27,那么两个球的表面积之比为（ ） A.8:27 B. 2:3 C.4:9 D. 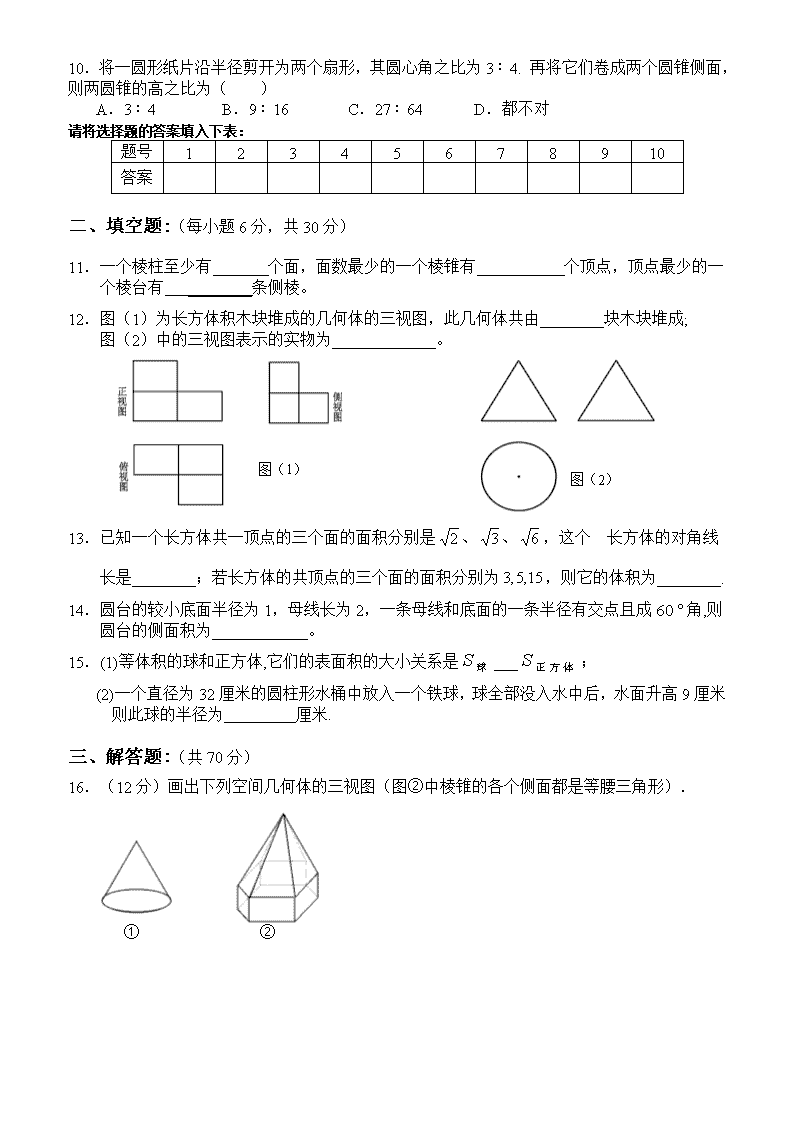2:9 7.有一个几何体的三视图及其尺寸如下（单位 cm），则该几何体的表面积及体积为：（ ） 6 5 俯视图 主视图 侧视图 A.24πcm2，12πcm3 B.15πcm2，12πcm3 C.24πcm2，36πcm3 D.以上都不正确 8．下列几种说法正确的个数是（ ） ①相等的角在直观图中对应的角仍然相等 ②相等的线段在直观图中对应的线段仍然相等 ③平行的线段在直观图中对应的线段仍然平行 ④线段的中点在直观图中仍然是线段的中点 A．1 B．2 C．3 D．4 9．正方体的内切球和外接球的半径之比为（ ） A． 3 :1 B． 3 : 2 C． 2: 3 D． 3 :3 10．将一圆形纸片沿半径剪开为两个扇形，其圆心角之比为 3∶4. 再将它们卷成两个圆锥侧面， 则两圆锥的高之比为（ ） A．3∶4 B．9∶16 C．27∶64 D．都不对 请将选择题的答案填入下表： 题号 1 2 3 4 5 6 7 8 9 10 答案 二、填空题:（每小题 6 分，共 30 分） 11．一个棱柱至少有 _____个面，面数最少的一个棱锥有 ________个顶点，顶点最少的一 个棱台有 ________条侧棱。 12．图（1）为长方体积木块堆成的几何体的三视图，此几何体共由________块木块堆成; 图（2）中的三视图表示的实物为_____________。 13．已知一个长方体共一顶点的三个面的面积分别是 2 、 3 、 6 ，这个 长方体的对角线 长是________；若长方体的共顶点的三个面的面积分别为3,5,15 ，则它的体积为________. 14．圆台的较小底面半径为 1，母线长为 2，一条母线和底面的一条半径有交点且成 60 角,则 圆台的侧面积为____________。 15．(1)等体积的球和正方体,它们的表面积的大小关系是 S 球 ___ S 正 方 体 ； (2)一个直径为 32 厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高 9 厘米 则此球的半径为_________厘米. 三、解答题:（共 70 分） 16．（12 分）画出下列空间几何体的三视图（图②中棱锥的各个侧面都是等腰三角形）． ① ② 图（1） 图（2） 17．（12 分）已知圆台的上下底面半径分别是 2、5,且侧面面积等于两底面面积之和,求该圆台 的母线长. 18. （14 分） （如图）在底半径为 2 ，母线长为 4 的圆锥中内接一个高为 3 的圆柱，求圆柱 的表面积. 19．（16 分）养路处建造圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用），已建的 仓库的底面直径为12M ，高 4M ，养路处拟建一个更大的圆锥形仓库，以存放更多食盐， 现有两种方案：一是新建的仓库的底面直径比原来大 4M（高不变）；二是高度增加 4M (底 面直径不变)。 （1） 分别计算按这两种方案所建的仓库的体积； （2） 分别计算按这两种方案所建的仓库的表面积； （3） 哪个方案更经济些？ 20．（16 分）根据给出的空间几何体的三视图，用斜二测画法画出它的直观图．（写出画法， 并保留作图痕迹） 正视图 侧视图 俯视图 高一数学必修 2 第一章测试题(答案) 一、选择题：（每小题 5 分，共 50 分） 1.A 2.C 3.D 4.B 5.A 6.C 7.A 8.B 9.D 10.D 二、填空题:（每小题 6 分，共 30 分） 11. 5,4,3. 符合条件的几何体分别是：三棱柱，三棱锥，三棱台 12. （1）4 （2）圆锥 13. 6 ，15 14. 6 画出圆台，则 1 2 1 21, 2, 2, ( ) 6r r l S r r l      圆台侧面 15. （1） 设 3 3 3 34 3, ,3 4 VV R a a V R     （2）12 2 3 34 , 64 27 123V Sh r h R R       三、解答题：（共 70 分） 16. （12 分）略 17. （12 分）解： 2 2 29(2 5) (2 5 ), 7l l     18. （14 分）解：圆锥的高 2 24 2 2 3h    ，圆柱的底面半径 1r  ， 2 2 3 (2 3)S S S         侧面表面 底面 　　 19. （16 分）解： （1）如果按方案一，仓库的底面直径变成16M ,则仓库的体积 2 3 1 1 1 16 2564 ( )3 3 2 3V Sh M          如果按方案二，仓库的高变成8M ，则仓库的体积 2 3 2 1 1 12 2888 ( )3 3 2 3V Sh M          （2）如果按方案一，仓库的底面直径变成16M ,半径为8M . 棱锥的母线长为 2 28 4 4 5l    则仓库的表面积 2 1 8 4 5 32 5 ( )S M     如果按方案二，仓库的高变成8M . 棱锥的母线长为 2 28 6 10l    则仓库的表面积 2 2 6 10 60 ( )S M     （3） 2 1V V ， 2 1S S 方案二比方案一更加经济 20. （16 分）解：由几何体的三视图知道，这个几何体是一个上面小而底面大的圆台，我们可以 先画出上、下底面圆，再画母线. 画法：（1）画轴 如下图， 画 x 轴、y 轴、z 轴 , 三轴相交于点 O，使 xOy=45°, xOz=90 °. z y′ A′ B′ A′ B′ x′ y A B x A B （2）画圆台的两底面 画出底面⊙O 假设交 x 轴于 A、B 两点，在 z 轴上截取 O′，使 OO ′等于三视图中相应高度，过 O′作 Ox 的平行线 O′x′，Oy 的平行线 O′y′利用 O′x′与 O′y′画出底面⊙O′，设⊙O′交 x′轴于 A′、B′两点. （3）成图 连接 A′A、B′B，去掉辅助线, 将被遮挡的部分要改为虚线，即得到给出三视 图所表示的直观图.