1. 您所在位置：首页 > 中小学教育 > 高中教育 > 教案 > 2020_2021学年新教材高中数学第四章指数函数与对数函数4

2020_2021学年新教材高中数学第四章指数函数与对数函数4 39页

  • 1.79 MB
  • 2021-06-16 发布

2020_2021学年新教材高中数学第四章指数函数与对数函数4

  • 39页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
  4. 网站客服QQ：403074932
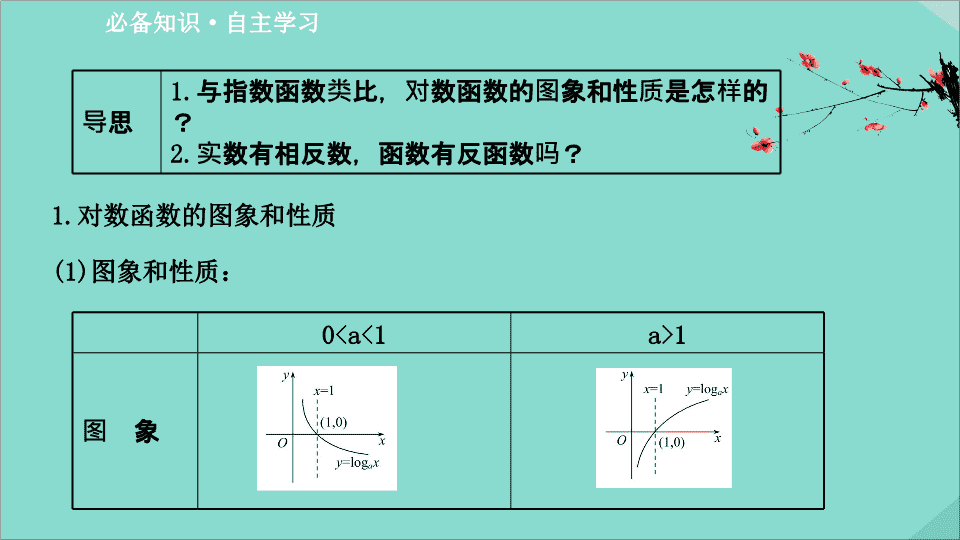
4.4.2 　对数函数的图象和性质 第 1 课时　对数函数的图象和性质　　　　 必备知识 · 自主学习 1. 对数函数的图象和性质 (1) 图象和性质： 导思 1. 与指数函数类比，对数函数的图象和性质是怎样的？ 2. 实数有相反数，函数有反函数吗？ 01 图　象 01 定义域 (0 ， +∞) 值　域 R 性　质 过定点 _______ 在 (0 ， +∞) 上是 _______ 在 (0 ， +∞) 上是 _______ (1 ， 0) 减函数 增函数 (2) 本质：作出不同底数的对数函数在同一个坐标系中的图象，观察这些图象的位置、公共点和变化趋势，它们的共性即对数函数的性质 . (3) 应用：①比较大小；②求定义域、值域；③解不等式； ④求参数的范围 . 【 思考 】 　对于对数函数 y=log 3 x ， y=log 5 x ， y= ， y= ， … ，为什么一定过点 (1 ， 0) ？ 提示： 当 x=1 时， log a 1=0 恒成立，即对数函数的图象一定过点 (1 ， 0). 2. 反函数 指数函数 y=a x (a>0 ，且 a≠1) 与对数函数 y=log a x(a>0 ，且 a≠1) 互为反函数， 它们的 _______ 与 _____ 正好互换 . 定义域 值域 【 思考 】 函数 y=log 3 x 与 y= 互为反函数吗？ 提示： 不是，同底数的指数函数与对数函数互为反函数 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”，错的打“ ×”) (1) 对数函数 y=log 5 x 与 y= 的图象关于 y 轴对称 . ( 　　 ) (2) 对数函数的图象都在 y 轴的右侧 . ( 　　 ) (3) 若对数函数 y=log (a-1) x 是减函数，则 a>2. ( 　　 ) 提示： (1)×. 两函数的图象关于 x 轴对称 . (2)√. 由对数函数的图象可知，正确 . (3)×. 由对数函数的单调性可知， 00 且 a≠1) 的图象恒过定点 P ，则 P 点的坐标是 _______.  【 解析 】 令 2x-3=1 ，解得 x=2 ，且 f(2)=log a 1=0 恒成立，所以函数 f(x) 的图象恒过定点 P(2 ， 0). 答案： (2 ， 0) 关键能力 · 合作学习 类型一　利用单调性比较大小 ( 逻辑推理 ) 【 题组训练 】 1. 已知 a=log 2 3 ， b=log 2 e ， c=ln 2 ，则 a ， b ， c 的大小关系是 ( 　　 ) A.a>b>c B.b>a>c C.c>b>a D.c>a>b 2.(2020· 遵义高一检测 ) 已知： a=log65 ， b=π0.3 ， c=ln ，则下列结论 正确的是 ( 　　 ) A.ab>c B.a>c>b C.b>a>c D.b>c>a 【 解析 】 1. 选 A.a=log 2 3>b=log 2 e>log 2 2=1 ， c=ln 2b>c. 2. 选 D. 因为 0=log 6 1π 0 =1 ， ln log 4 20>2 ，且 log 6 30b>c. 【 解题策略 】 比较对数值大小时常用的四种方法 (1) 同底数的利用对数函数的单调性 . (2) 同真数的利用对数函数的图象或用换底公式转化 . (3) 底数和真数都不同，找中间量 . (4) 若底数为同一参数，则根据底数对对数函数单调性的影响，对底数进行分类讨论 . 提醒：比较数的大小时先利用性质比较出与 0 或 1 的大小 . 【 补偿训练 】 (2020· 鄂尔多斯高一检测 ) 已知 a= ， b=log 4 5 ， c=0.5 0.4 ， 则 ( 　　 ) A.alog 4 4=1 ， 0<0.5 0.4 <0.5 0 =1 ，所以 a0 ，且 a≠1) 的图象可能是 ( 　　 ) 2.(2020· 珠海高一检测 ) 若函数 f(x)=log a (x+m)+1(a>0 ，且 a≠1) 恒过定点 (2 ， n) ，则 m+n 的值为 _______.  【 思路导引 】 1. 先对 a 分两种情况讨论，再利用平移检验图象是否符合 . 2. 将定点坐标代入求 m ， n. 【 解析 】 1. 选 D. 当 01 时，函数 y=a x 过定点 (0 ， 1) 且单调递 增，则函数 y= 过定点 (0 ， 1) 且单调递减，函数 y=log a 过定点 且 单调递增，各选项均不符合 . 2. 依题意 log a (2+m)+1=n 为定值， 可得 2+m=1 ，即 m=-1 ，所以 n=1 ， m+n=0. 答案： 0 【 解题策略 】 1. 对数函数底数对图象的影响 其中 a ， b ， c ， d 是图象对应的对数函数的底数， 根据图象，其大小关系为 00 ，且 a≠1) 的图象过定点时，只需令 f(x)=1 求出 x ，即得定点为 (x ， m). 【 跟踪训练 】 　在同一直角坐标系中，函数 f(x)=x a (x≥0) ， g(x)=log a x(a>0 且 a≠1) 的图象可能是 ( 　　 ) 【 解析 】 选 D. 对于 A 项，对数函数的图象过 (1 ， 0) 点，但是幂函数的图象不过 (0 ， 1) 点，所以 A 项不满足要求；对于 B 项，由图象知，幂函数中 a>1 ，对数函数中 01 ，矛盾，所以 C 项不满足要求； 对于 D 项，由图象知幂函数与对数函数中 01 时，解得 x≤ ，不成立； 当 00 ，且 a≠1) 的最大值比最小值大 1 ，则底数 a 的值为 ( 　　 ) 【 思路导引 】 分两种情况分别表示出最大值、最小值后列式求值 . 【 解析 】 选 AB. 当 01 时，函数 f(x) 在 [2 ， π] 上是增函数， 故 log a π-log a 2=1 ，故 a= . 【 解题策略 】 与对数函数值域相关的问题 (1) 利用对数函数的单调性求值域是解决问题的主要方法； (2) 若底数中含有字母，需要对底数分大于 1 ，小于 1 大于 0 两种情况讨论 . 【 题组训练 】 1. 已知函数 f(x)= 的值域为 [-1 ， 1] ，则函数 f(x) 的定义域是 ( 　　 ) 2. 函数 y= 的定义域为 _______.  【 解析 】 1. 选 A. 因为已知函数的值域为 [-1 ， 1] ， 所以 ，化简解得 ， 故函数 f(x) 的定义域为 . 2. 由题意得 log 2 (3x+1)≤2 ，则 0<3x+1≤4 ， 解得

您可能关注的文档

相关文档

最近下载