高中数学必修2教案：4_1_1圆的标准方程。doc 3页

‎4.1.1‎ 圆的标准方程 三维目标：‎ 知识与技能：1、掌握圆的标准方程，能根据圆心、半径写出圆的标准方程。‎ ‎2、会用待定系数法求圆的标准方程。‎ 过程与方法：进一步培养学生能用解析法研究几何问题的能力，渗透数形结合思想，通过圆的标准方程解决实际问题的学习，注意培养学生观察问题、发现问题和解决问题的能力。‎ 情感态度与价值观：通过运用圆的知识解决实际问题的学习，从而激发学生学习数学的热情和兴趣。‎ 教学重点：圆的标准方程 教学难点：会根据不同的已知条件，利用待定系数法求圆的标准方程。‎ 教学过程：‎ ‎1、情境设置：‎ 在直角坐标系中，确定直线的基本要素是什么？圆作为平面几何中的基本图形，确定它的要素又是什么呢？什么叫圆？在平面直角坐标系中，任何一条直线都可用一个二元一次方程来表示，那么，原是否也可用一个方程来表示呢？如果能，这个方程又有什么特征呢？‎ 探索研究：‎ ‎2、探索研究：‎ 确定圆的基本条件为圆心和半径，设圆的圆心坐标为A(a,b)，半径为r。（其中a、b、r都是常数，r>0）设M(x,y)为这个圆上任意一点，那么点M满足的条件是（引导学生自己列出）P={M||MA|=r},由两点间的距离公式让学生写出点M适合的条件 ①‎ 化简可得： ②‎ 引导学生自己证明为圆的方程，得出结论。‎ 方程②就是圆心为A(a,b),半径为r的圆的方程，我们把它叫做圆的标准方程。‎ ‎3、知识应用与解题研究 例（1）：写出圆心为半径长等于5的圆的方程，并判断点是否在这个圆上。‎ 分析探求：可以从计算点到圆心的距离入手。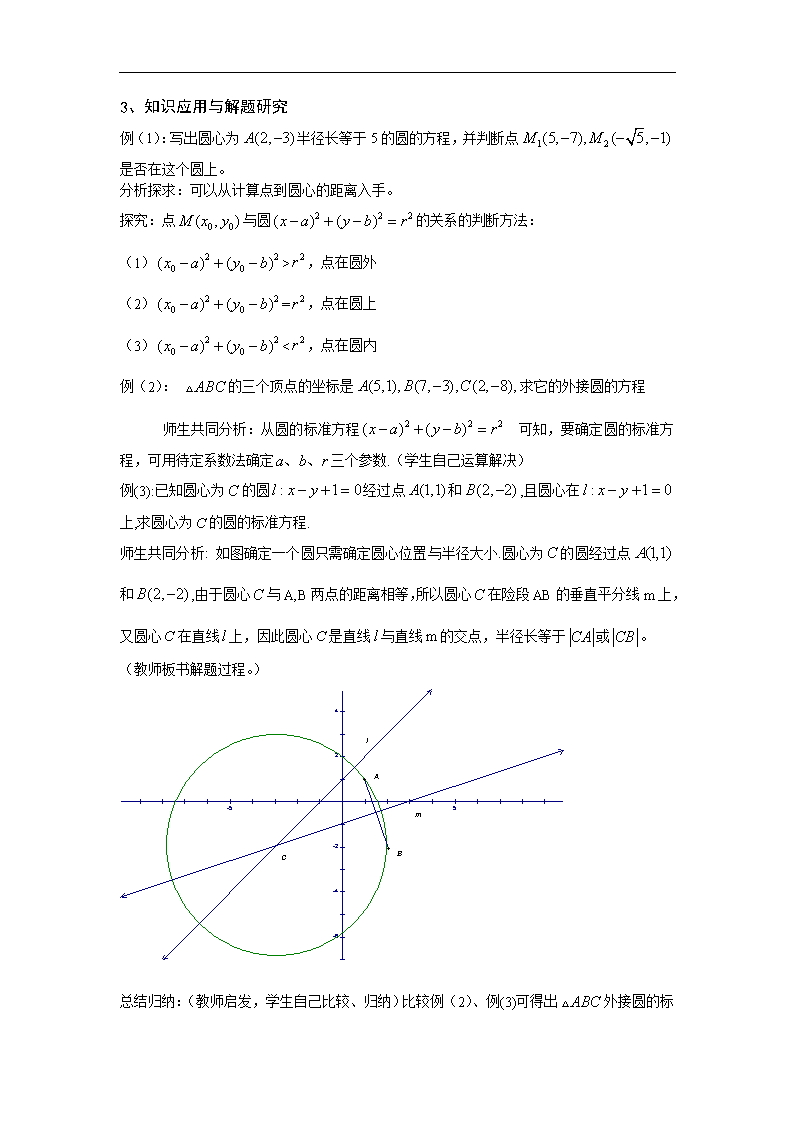‎ 探究：点与圆的关系的判断方法：‎ ‎（1）>，点在圆外 ‎（2）=，点在圆上 ‎（3）<，点在圆内 例（2）： 的三个顶点的坐标是求它的外接圆的方程 ‎ 师生共同分析：从圆的标准方程 可知，要确定圆的标准方程，可用待定系数法确定三个参数.（学生自己运算解决）‎ 例(3):已知圆心为的圆经过点和,且圆心在上,求圆心为的圆的标准方程.‎ 师生共同分析: 如图确定一个圆只需确定圆心位置与半径大小.圆心为的圆经过点和,由于圆心与A,B两点的距离相等，所以圆心在险段AB的垂直平分线m上，又圆心在直线上，因此圆心是直线与直线m的交点，半径长等于或。‎ ‎（教师板书解题过程。） ‎ 总结归纳：（教师启发，学生自己比较、归纳）比较例（2）、例(3)可得出 外接圆的标准方程的两种求法：‎ ①、 根据题设条件，列出关于的方程组，解方程组得到得值，写出圆的标准方程.‎ 根据确定圆的要素，以及题设条件，分别求出圆心坐标和半径大小，然后再写出圆的标准方程.‎ 练习：课本第1、3、4题 提炼小结：‎ 1、 圆的标准方程。‎ 2、 点与圆的位置关系的判断方法。‎ 3、 根据已知条件求圆的标准方程的方法。‎ 作业：课本习题4.1第2、3、4题