人教新课标A版数学高三高考卷 05高考理科数学（浙江卷）试题及答案 11页

2005 年高考理科数学 浙江卷 试题及答案 第Ⅰ卷 (选择题 共 60 分) 一、选择题：本大题共 10 小题，每小题 5 分，共 50 分 在每小题给出的四个选项中， 只有一项是符合题目要求的 1． limn 2 1 2 3 n n     ＝( ) (A) 2 (B) 4 (C) 2 1 (D)0 2．点(1，－1)到直线 x－y＋1＝0 的距离是( ) (A) 2 1 (B) 3 2 (C) 2 2 (D) 3 2 2 3．设 f(x)＝ 2 | 1| 2,| | 1, 1 , | | 11 x x xx      ，则 f[f( 2 1 )]＝( ) (A) 2 1 (B) 4 13 (C)－ 9 5 (D) 25 41 4．在复平面内，复数 1 i i ＋(1＋ 3 i)2 对应的点位于( ) (A) 第一象限 (B) 第二象限 (C) 第三象限 (D)第四象限 5．在(1－x)5＋(1－x)6＋(1－x)7＋(1－x)8 的展开式中，含 x3 的项的系数是( ) (A) 74 (B) 121 (C) －74 (D) －121 6．设 、 为两个不同的平面，l、m 为两条不同的直线，且 l   ，m   ，有如下的 两个命题：①若 ∥  ，则 l∥m；②若 l⊥m，则 ⊥  ．那么 (A) ①是真命题，②是假命题 (B) ①是假命题，②是真命题 (C) ①②都是真命题 (D) ①②都是假命题 7．设集合  ( , ) | , ,1A x y x y x y ＝ 是三角形的三边长 ，则 A 所表示的平面区域(不含 边界的阴影部分)是( ) (A) (B) (C) (D) 8．已知 k＜－4，则函数 y＝cos2x＋k(cosx－1)的最小值是( ) (A) 1 (B) －1 (C) 2k＋1 (D) －2k＋1 9．设 f(n)＝2n＋1(n∈N)，P＝{1，2，3，4，5}，Q＝{3，4，5，6，7}，记 P  ＝{n∈N|f(n) ∈P}，Q  ＝{n∈N|f(n)∈Q}，则( P  ∩ Nð Q  )∪(Q  ∩ Nð P  )＝( ) (A) {0，3} (B){1，2} (C) (3，4，5} (D){1，2，6，7} 10．已知向量 a  ≠ e  ，| e  |＝1，对任意 t∈R，恒有| a  －t e  |≥| a  － e  |，则 (A) a  ⊥ e  (B) a  ⊥( a  － e  ) (C) e  ⊥( a  － e  ) (D) ( a  ＋ e  )⊥( a  － e  ) 第Ⅱ卷 (非选择题 共 100 分) 二、填空题：本大题共 4 小题，每小题 4 分，共 16 分 把答案填在答题卡的相应位置 11．函数 y＝ 2 x x  (x∈R，且 x≠－2)的反函数是_________． 12．设 M、N 是直角梯形 ABCD 两腰的中点，DE⊥AB 于 E(如 图)．现将△ADE 沿 DE 折起，使二面角 A－DE－B 为 45°，此 时点 A 在平面 BCDE 内的射影恰为点 B，则 M、N 的连线与 AE 所成角的大小等于_________． 13．过双曲线 2 2 2 2 1x y a b   (a＞0，b＞0)的左焦点且垂直于 x 轴的直线与双曲线相交于 M、N 两点，以 MN 为直径的圆恰好过双曲线的右顶点，则双曲 线的离心率等于_________． 14．从集合{O，P，Q，R，S}与{0，1，2，3，4，5，6，7，8，9}中各任取 2 个元素排成 一排(字母和数字均不能重复)．每排中字母 O，Q 和数字 0 至多只能出现一个的不同排法 种数是_________．(用数字作答)． 三、解答题：本大题共 6 小题，每小题 14 分，共 84 分 解答应写出文字说明，证明过程 或演算步骤 15．已知函数 f(x)＝－ 3 sin2x＋sinxcosx． (Ⅰ) 求 f( 25 6  )的值； (Ⅱ) 设 ∈(0， )，f( 2  )＝ 4 1 － 3 2 ，求 sin 的值． 16．已知函数 f(x)和 g(x)的图象关于原点对称，且 f(x)＝x2＝2x． M N D C B A (Ⅰ)求函数 g(x)的解析式； (Ⅱ)解不等式 g(x)≥f(x)－|x－1|． 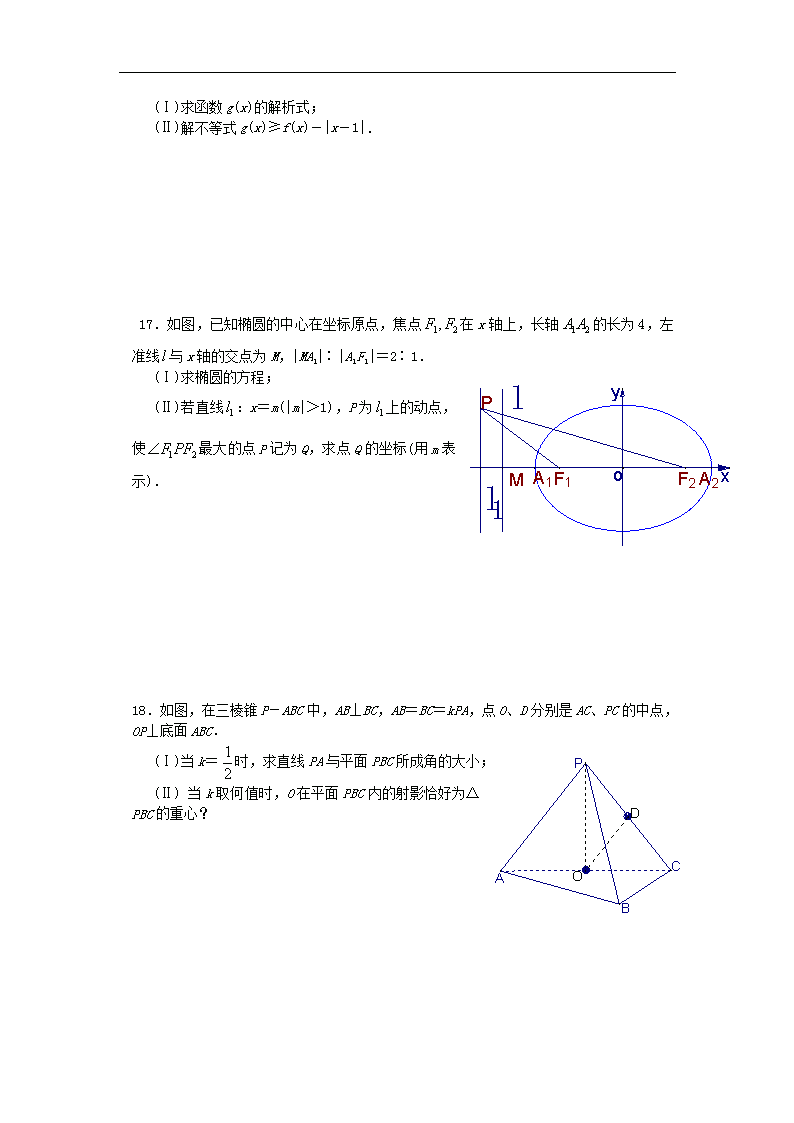17．如图，已知椭圆的中心在坐标原点，焦点 1 2,F F 在 x 轴上，长轴 1 2A A 的长为 4，左 准线l 与 x 轴的交点为 M，|MA1|∶|A1F1|＝2∶1． (Ⅰ)求椭圆的方程； (Ⅱ)若直线 1l ：x＝m(|m|＞1)，P 为 1l 上的动点， 使 1 2F PF 最大的点 P 记为 Q，求点 Q 的坐标(用 m 表 示)． 18．如图，在三棱锥 P－ABC 中，AB⊥BC，AB＝BC＝kPA，点 O、D 分别是 AC、PC 的中点， OP⊥底面 ABC． (Ⅰ)当 k＝ 2 1 时，求直线 PA 与平面 PBC 所成角的大小； (Ⅱ) 当 k 取何值时，O 在平面 PBC 内的射影恰好为△ PBC 的重心？ l l 1 A 2 A 1 F 2 P F 1 M o y x D O A B C P 19．袋子 A 和 B 中装有若干个均匀的红球和白球，从 A 中摸出一个红球的概率是 3 1 ，从 B 中摸出一个红球的概率为 p． (Ⅰ) 从 A 中有放回地摸球，每次摸出一个，有 3 次摸到红球即停止．(i)求恰好摸 5 次 停止的概率；(ii)记 5 次之内(含 5 次)摸到红球的次数为 ，求随机变量 的分布率及数 学期望 E ． (Ⅱ) 若 A、B 两个袋子中的球数之比为 12，将 A、B 中的球装在一起后，从中摸出一 个红球的概率是 2 5 ，求 p 的值． 20．设点 nA ( nx ，0)， 1( ,2 )n n nP x  和抛物线 nC ：y＝x2＋an x＋bn(n∈N*)，其中 an＝－ 2－4n－ 1 1 2n ， nx 由以下方法得到： x1＝1，点 P2(x2，2)在抛物线 C1：y＝x2＋a1x＋b1 上，点 A1(x1，0)到 P2 的距离是 A1 到 C1 上点的最短距离，…，点 1 1( ,2 )n n nP x  在抛物线 nC ：y＝x2＋an x＋bn 上，点 nA ( nx ，0) 到 1nP  的距离是 nA 到 nC 上点的最短距离． (Ⅰ)求 x2 及 C1 的方程． (Ⅱ)证明{ nx }是等差数列． 2005 年高考理科数学 浙江卷 试题及答案 参考答案 一、选择题：本题考查基本知识和基本运算 每小题 5 分，满分 50 分 （1）C （2）D （3）B （4）B （5）D （6）D （7）A （8）A （9）A （10）C 二、填空题：本题考查基本知识和基本运算 每小题 4 分，满分 16 分 （11）  2 , 11 xy x R xx    且 ；（12）90 ；（13）2；（14）8424 三、解答题： （15）本题主要考查三角函数的诱导公式、倍角公式等基础知识和基本的运算能力 满分 14 分 解：（1） 25 1 25 3sin ,cos6 2 6 2    ， 225 25 25 253sin sin cos 06 6 6 6f            （2）   3 3 1cos2 sin 22 2 2f x x x   3 1 3 1 3cos sin2 2 2 2 4 2f            216sin 4sin 11 0    ， 解得 1 3 5sin 8    0, , sin 0     故 1 3 5sin 8   （16）本题主要考查函数图象的对称、中点坐标公式、解不等式等基础知识，以及运算和 推理能力 满分 14 分 解：(Ⅰ)设函数  y f x 的图象上任意一点  0 0,Q x y 关于原点的对称点为  ,P x y ，则 0 0 0 0 0, ,2 .0,2 x x x x y y y y         即 ∵点  0 0,Q x y 在函数  y f x 的图象上 ∴  2 2 22 2 , 2y x x y x x g x x x        ，即 故 (Ⅱ)由     21 2 1 0g x f x x x x     ， 可得 当 1x  时， 22 1 0x x   ，此时不等式无解 当 1x  时， 22 1 0x x   ，解得 11 2x   因此，原不等式的解集为 11, 2     （17）本题主要考查椭圆的几何性质、椭圆方程、两条直线的夹角，点的坐标等基础知识， 考查解析几何的基本思想方法和综合解题能力 满分 14 分 解：(Ⅰ)设椭圆方程为   2 2 2 2 1 0x y a ba b     ，半焦距为 c ，则 2 1 1 1,aMA a A F a cc       2 2 2 2 2 2 4 a a a cc a a b c           由题意,得 2, 3, 1a b c    2 2 1.4 3 x y 故椭圆方程为 (Ⅱ) 设  0, ,| | 1P m y m  ， 当 0 0y  时， 1 2 0F PF  ； 当 0 0y  时， 2 2 10 2F PF PF M      ， 只需求 2 2tan F PF 的最大值即可 设直线 1PF 的斜率 0 1 1 yk m   ，直线 2PF 的斜率 0 2 1 yk m   ， 0 02 1 2 2 2 2 2 2 1 2 0 0 2 | | 2 | | 1tan 1 1 2 1 | | 1 y yk kF PF k k m y m y m            当且仅当 2 01 | |m y  时， 1 2F PF 最大，  2, 1 ,| | 1Q m m m    （18）本题主要考查空间线面关系、空间向量的概念与运算等基础知识，同时考查空间想 象能力和推理运算能力 满分 14 分 解：方法一： (Ⅰ) ∵O、D 分别为 AC、PC 中点， OD PA ∥ PA PAB又 平面 ， OD PAB 平面∥ (Ⅱ) AB BC OA OC  ， ， OA OB OC   ， OP ABC又 平面 ， .PA PB PC   E PE BC POE取BC中点 ，连结 ，则 平面 OF PE F DF OF PBC 作 于 ，连结 ，则 平面 ODF OD PBC  是 与平面 所成的角. 又OD PA∥ ， PA 与平面 PBC 所成的角的大小等于 ODF ， 210sin ,30 OFRt ODF ODF OD    在 中， 210arcsin .30PBC PA与平面 所成的角为 （Ⅲ）由(Ⅱ)知，OF PBC 平面 ，∴F 是 O 在平面 PBC 内的射影 ∵D 是 PC 的中点， 若点 F 是 PBC 的重心，则 B，F，D 三点共线， ∴直线 OB 在平面 PBC 内的射影为直线 BD， , ,OB PC PC BD PB PC     ，即 1k  反之，当 1k  时，三棱锥O PBC 为正三棱锥， ∴O 在平面 PBC 内的射影为 PBC 的重心 方法二： OP ABC 平面 ， ,OA OC AB BC  ， E F D O B C A P , , .OA OB OA OP OB OP    以 O 为原点，射线 OP 为非负 z 轴，建立空间直角坐标系O xyz （如图） 设 ,AB a 则 2 2 2,0,0 , 0, ,0 , ,0,02 2 2A a B C                      ， 设OP h ，则  0,0,P h (Ⅰ)D 为 PC 的中点， 2 1,0,4 2OD a h         ， 又 2 1,0, , , //2 2PA a h OD PA OD PA               ， OD PAB 平面∥ (Ⅱ) 1 2k  ，即 7 2 72 , , ,0,2 2 2PA a h a PA a a            ， 可求得平面 PBC 的法向量 11, 1, 7n         ， 210cos , 30| | | | PA nPA n PA n            ， 设 PA 与平面 PBC 所成的角为 ，则 210sin | cos , | 30PA n      ， （Ⅲ） PBC 的重心 2 2 1, ,6 6 3G a a h      ， 2 2 1, ,6 6 3OG a a h         ， ,OG PBC OG PB     平面 ， 又 2 22 1 1 20, , , 0,2 6 3 2PB a h OG PB a h h a                 ， 2 2PA OA h a    ，即 1k  ， D O B C A P x y z 反之，当 1k  时，三棱锥O PBC 为正三棱锥， ∴O 在平面 PBC 内的射影为 PBC 的重心 （19）本题主要考查相互独立事件同时发生的概率和随机变量的分布列、数学期望等概念， 同时考查学生的逻辑思维能力 满分 14 分 解：(Ⅰ)（i） 2 2 2 4 1 2 1 8 3 3 3 81C              (ii)随机变量 的取值为 0，1，2，3，； 由 n 次独立重复试验概率公式    1 n kk k n nP k C p p   ，得   5 0 5 1 320 1 3 243P C         ；   4 1 5 1 1 801 13 3 243P C            2 3 2 5 1 1 802 13 3 243P C                  3 2 3 5 1 1 173 13 3 243P C                （或   32 80 2 173 1 243 243P       ） 随机变量 的分布列是  0 1 2 3 P 32 243 80 243 80 243 17 243  的数学期望是 32 80 80 17 1310 1 2 3243 243 243 243 81E          (Ⅱ)设袋子 A 中有 m 个球，则袋子 B 中有 2m 个球 由 1 2 23 3 5 m mp m   ，得 13 30p  （20）本题主要考查二次函数的求导、导数的应用、等差数列、数学归纳法等基础知识， 以及综合运用所学知识分析和解决问题的能力 满分 14 分 解：（Ⅰ）由题意得   2 1 1 11,0 , : 7A C y x x b   ， 设点  ,P x y 是 1C 上任意一点， 则      22 22 2 1 1| | 1 1 7A P x y x x x b        令      22 2 11 7f x x x x b     则       2 12 1 2 7 2 7f x x x x b x       由题意得  2 0f x  ， 即     2 2 2 1 22 1 2 7 2 7 0x x x b x      又  2 2 ,2P x 在 1C 上， 2 2 2 12 7x x b    解得 2 13, 14x b  故 1C 的方程为 2 7 14y x x   (Ⅱ)设点  ,P x y 是 nC 上任意一点， 则      22 22 2| |n n n n nA P x x y x x x a x b        令      22 2 n n ng x x x x a x b     则       22 2 2n n n ng x x x x a x b x a       由题意得  1 0ng x   即     2 1 1 12 2 2 0n n n n n n nx x x a x b x a        又 1 2 12 n n n n nx a x b    ，      1 12 2 0 1n n n n nx x x a n       ， 即   1 11 2 2 0 *n n n n nx x a     下面用数学归纳法证明 2 1nx n  ， ①当 1n  时， 1 1x  ，等式成立； ②假设当 n k 时，等式成立，即 2 1kx k  ， 则当 1n k  时，由 * 知 1 11 2 2 0k k k k kx x a     ， 又 1 12 4 2k ka k     ， 1 1 2 2 11 2 k k k k k x ax k      ， 即 1n k  时，等式成立 由①②知，等式对 *n N 成立， 故 nx 是等差数列