浙江省2021届高考数学一轮复习第三章函数概念及基本初等函数Ⅰ第6节幂函数指数函数对数函数课件 37页

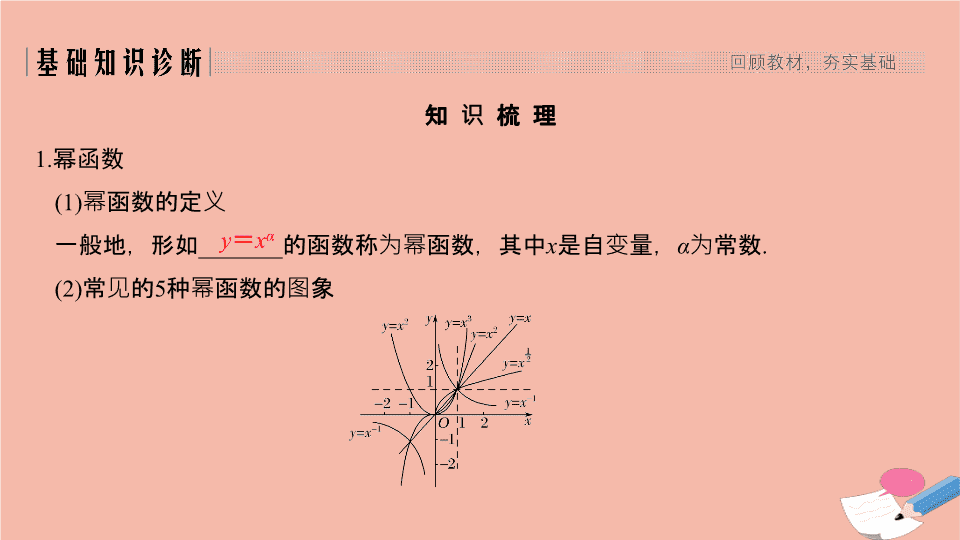
第 6 节　幂函数、指数函数、对数函数 知 识 梳 理 1 . 幂函数 (1) 幂函数的定义 一般地，形如 _______ 的函数称为幂函数，其中 x 是自变量， α 为常数 . (2) 常见的 5 种幂函数的图象 y ＝ x α (3) 常见的 5 种幂函数的性质 [0 ，＋ ∞ ) { y | y ∈ R ， 且 y ≠ 0} 2. 指数函数及其性质 (1) 概念：函数 y ＝ a x ( a >0 且 a ≠ 1) 叫做指数函数，其中指数 x 是自变量，函数的定义域是 R ， a 是底数 . (2) 指数函数的图象与性质   a >1 0< a <1 图象 定义域 R 值域 __________ 性质 过 定点 ________ ， 即 x ＝ 0 时， y ＝ 1 当 x >0 时， _______ ； 当 x <0 时 ， _________ 当 x <0 时 ， _______ ； 当 x >0 时 ， _______ 在 ( － ∞ ，＋ ∞ ) 上 是 ________ 在 ( － ∞ ，＋ ∞ ) 上 是 ________ (0 ，＋ ∞ ) (0 ， 1) y >1 0< y <1 y >1 0< y <1 增函数 减函数 3. 对数函数及其性质 (1) 概念：函数 y ＝ log a x ( a >0 ，且 a ≠ 1) 叫做对数函数，其中 x 是自变量，函数的定义域是 (0 ，＋ ∞ ). (2) 对数函数的图象与性质   a >1 0< a <1 图象 性质 定义域 ： _________ 值域 ： _____ 当 x ＝ 1 时， y ＝ 0 ，即过 定点 _______ 当 x >1 时 ， _______ ； 当 0< x <1 时 ， _______ 当 x >1 时 ， _______ ； 当 0< x <1 时 ， _______ 在 (0 ，＋ ∞ ) 上 是 ________ 在 (0 ，＋ ∞ ) 上 是 ________ (0 ，＋ ∞ ) R (1 ， 0) y >0 y <0 y <0 y >0 增函数 减函数 4. 反函数 指数函数 y ＝ a x ( a >0 ，且 a ≠ 1) 与对数函数 （ a >0 ，且 a ≠ 1) 互为反函数，它们的图象关于直线 对称 . y ＝ log a x y ＝ x [ 常用结论与易错提醒 ] 1. 幂函数满足三个条件： (1) 幂底是单自变量； (2) 指数为常数； (3) 系数为 1. 类似地指数函数、对数函数也分别满足三个条件 . 2.(1) 幂函数图象的分布规律：作一直线 x ＝ t >1 ，与幂函数交点在上面的幂函数的指数大； (2) 指数函数图象的分布规律：作一直线 x ＝ t >0 ，与指数函数交点在上面的指数函数的底数大； (3) 对数函数图象的分布规律：作一直线 y ＝ k >0 ，与对数函数交点在右边的对数函数的底数大 . 解析　 (1) 错误， y ＝ 1 的图象去掉点 (0 ， 1) 才是 y ＝ x 0 的图象； 答案　 (1) × 　 (2) × 　 (3) × 　 (4) × 解析　 当 0< a <1 时，函数 y ＝ a x 的图象过定点 (0 ， 1) ，在 R 上单调递减， 显然 A ， B ， C ， D 四个选项都不符合 . 故选 D. 答案 　 D 3. ( 一题多解 ) 已知函数 y ＝ log a ( x ＋ c )( a ， c 为常数，其中 a >0 ，且 a ≠ 1) 的图象如图，则下列结论成立的是 ( 　　 ) A. a >1 ， c >1 B. a >1 ， 0< c <1 C.0< a <1 ， c >1 D.0< a <1 ， 0< c <1 解析　法一 　由题图可知，函数在定义域内为减函数，所以 0< a <1. 又当 x ＝ 0 时， y >0 ，即 log a c >0 ，所以 0< c <1. 法二 　由图可知， y ＝ log a ( x ＋ c ) 的图象是由 y ＝ log a x 的图象向左平移 c ( c ＞ 0) 个单位而得到的，其中 0 ＜ c ＜ 1 ，再根据单调性易知 0 ＜ a ＜ 1. 答案　 D 答案　 2 5. 若幂函数 y ＝ ( m 2 － 3 m ＋ 3) x m 2 － m － 2 的图象不经过原点，则实数 m 的值为 ________. 答案　 1 或 2 6. 当 a >0 ，且 a ≠ 1 时，函数 f ( x ) ＝ a x － 3 － 2 必过定点 ________ ，其值域为 ________. 解析　 函数 f ( x ) ＝ a x － 3 － 2 的图象是将函数 y ＝ a x 的图象向右平移 3 个单位，再向下平移 2 个单位得到的 . 故函数 f ( x ) ＝ a x － 3 － 2 必过定点 (3 ，－ 1) ，其值域为 ( － 2 ，＋ ∞ ). 答案　 (3 ，－ 1) 　 ( － 2 ，＋ ∞ ) 考点一　幂函数 解析　 (1) 由 f ( x ) 为奇函数，所以 α ＝－ 1 ， 1 ， 3 ，又在 (0 ，＋ ∞ ) 上为递减可知 α ＝－ 1. 答案　 (1) － 1 　 (2)B 规律方法 　 (1) 可以借助幂函数的图象理解函数的对称性、单调性； (2) 在比较幂值的大小时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较，准确掌握各个幂函数的图象和性质是解题的关键 . 答案　 (1)C 　 (2)A 　 (3)D 考点二　指数函数 令 u ＝－ x 2 － 4 x ＋ 3 ＝－ ( x ＋ 2) 2 ＋ 7. 即当 f ( x ) 有最大值 3 时， a 的值等于 1. (3) 由 f ( x ) 的值域是 (0 ，＋ ∞ ) 知， ax 2 － 4 x ＋ 3 的值域为 R ，则必有 a ＝ 0. 规律方法 　 (1) 求解与指数函数有关的复合函数问题，首先要熟知指数函数的定义域、值域、单调性等相关性质，其次要明确复合函数的构成，涉及值域、单调区间、最值等问题时，都要借助 “ 同增异减 ” 这一性质分析判断 . (2) 比较指数式的大小的方法是： ① 能化成同底数的先化成同底数幂，再利用单调性比较大小； ② 不能化成同底数的，一般引入 “ 1 ” 等中间量比较大小； ③ 当底数 a 与 “ 1 ” 的大小关系不确定时，要分类讨论 . 解析　 (1) 因为 0< a < b <1 ，所以 0<1 － b <1 － a <1 ，则 (1 － a ) a >(1 － a ) b >(1 － b ) b ，故选 D. (3) 曲线 | y | ＝ 2 x ＋ 1 与直线 y ＝ b 的图象如图所示，由图象可知：如果 | y | ＝ 2 x ＋ 1 与直线 y ＝ b 没有公共点，则 b 应满足的条件是 b ∈ [ － 1 ， 1]. 答案　 (1)D 　 (2)( － ∞ ， 27] 　 (3)[ － 1 ， 1] 考点三　对数函数 所以函数的定义域为 ( － ∞ ， 0) ∪ (2 ，＋ ∞ ) ，结合图象可得函数的单调递减区间为 (2 ，＋ ∞ ) ，单调递增区间为 ( － ∞ ， 0). ① 当 0< a <1 时，要使函数 f ( x ) 在区间 [2 ， 4] 上是增函数，则 g ( x ) ＝ ax 2 － x 在 [2 ， 4] 上单调递减，且 g ( x ) min >0 ， ② 当 a >1 时，要使函数 f ( x ) 在区间 [2 ， 4] 上是增函数，则 g ( x ) ＝ ax 2 － x 在 [2 ， 4] 上单调递增，且 g ( x ) min >0 ， 又 a >1 ，所以 a >1 ，综上可得 a >1. 实数 a 的取值范围为 (1 ，＋ ∞ ). 规律方法 　 (1) 确定函数的定义域，研究或利用函数的性质，都要在其定义域上进行 . (2) 如果需将函数解析式变形，一定要保证其等价性，否则结论错误 . (3) 在解决与对数函数相关的比较大小或解不等式问题时，要优先考虑利用对数函数的单调性来求解 . 在利用单调性时，一定要明确底数 a 的取值对函数增减性的影响，及真数必须为正的限制条件 . 当 a >1 时，不符合题意，舍去 . 答案　 (1)A 　 (2)B 　 (3)C